Java算法之排序

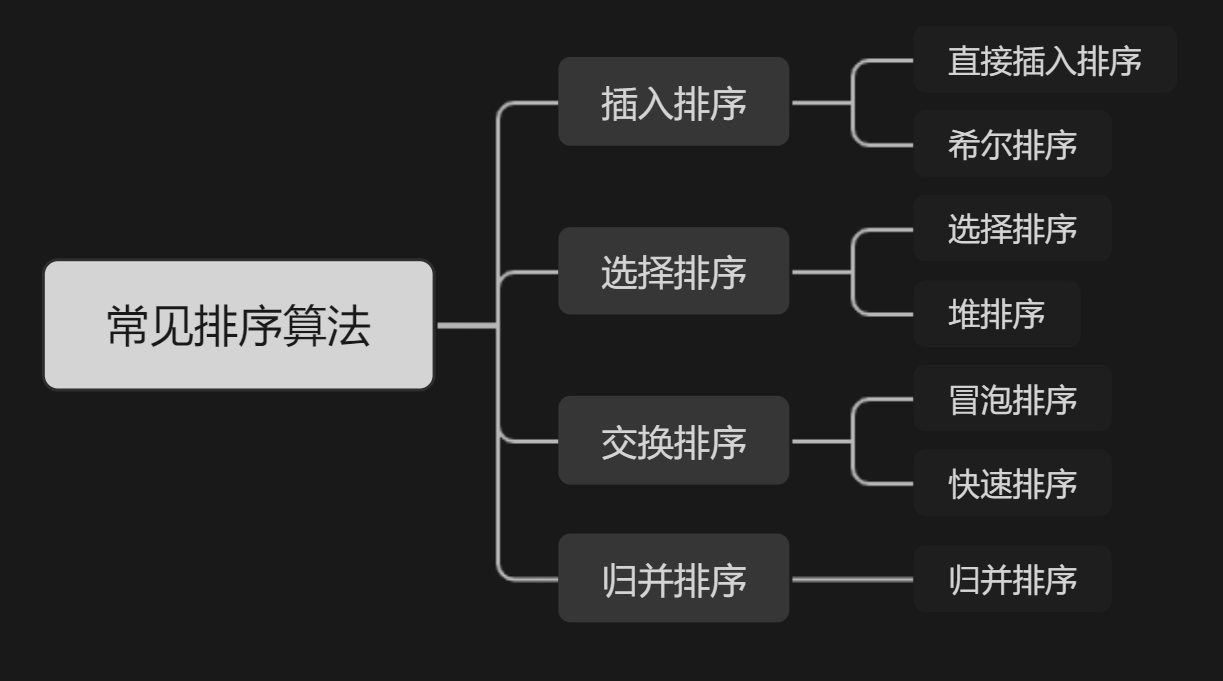
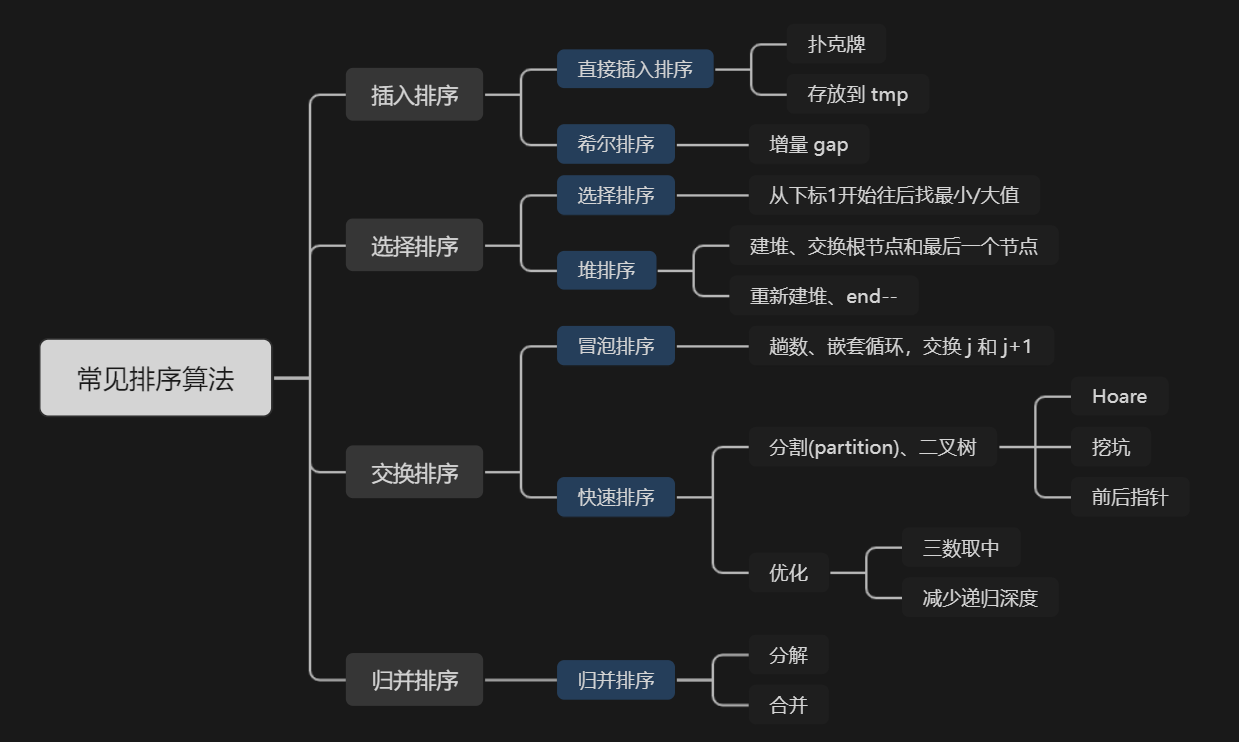
????????下面我們將講述七大基于比較的排序算法的基本原理及實現。并從穩定性、時間復雜度、空間復雜度3種性能對每種排序進行分析。
重點：快速排序和堆排序；難點：快速排序和歸并排序

一、排序概念

二、常見排序算法的實現

2.1 插入排序

2.1.1 直接插入排序

2.1.2 希爾排序（縮小增量排序）

2.2 選擇排序

2.2.1 直接選擇排序

2.2.2 直接選擇排序優化

2.2.3 堆排序

2.3 交換排序

2.3.1 冒泡排序

2.3.2 快速排序

1、Hoare 法

2、🔴挖坑法

3、前后指針

2.3.3 快速排序優化

1、三數取中法

2、減少遞歸深度

2.3.4 快速排序非遞歸

2.4 歸并排序

2.4.1?

2.4.2 歸并排序非遞歸實現

三、特性總結

四、其他非基于比較排序

4.1 計數排序

一、排序概念

????????穩定性：假定在待排序的記錄序列中，存在多個具有相同的關鍵字的記錄，若經過排序，這些記錄的相對次序保持不變，即在原序列中，r[i]=r[j]，且 r[i] 在 r[j] 之前，而在排序后的序列中，r[i] 仍在r[j] 之前，則稱這種排序算法是穩定的；否則稱為不穩定的。

內部排序：數據元素全部放在內存中的排序。

外部排序：數據元素太多不能同時放在內存中，根據排序過程的要求在內外村之間移動數據的排序，例如磁盤上的排序。

二、常見排序算法的實現

2.1 插入排序

2.1.1 直接插入排序

? ? ? ? 基本思想：把待排序的記錄按其關鍵碼值的大小逐個插入到一個已經排好序的有序序列中，直到所有的記錄插入完為止，得到一個新的有序序列。例如玩撲克牌前對手里的牌進行整理。

比如現在你手上有一副卡牌，不看花色：10、2、9、4、7，從左往右的第2張發現比第一張小，因此將其抽出插到第一張的前面。

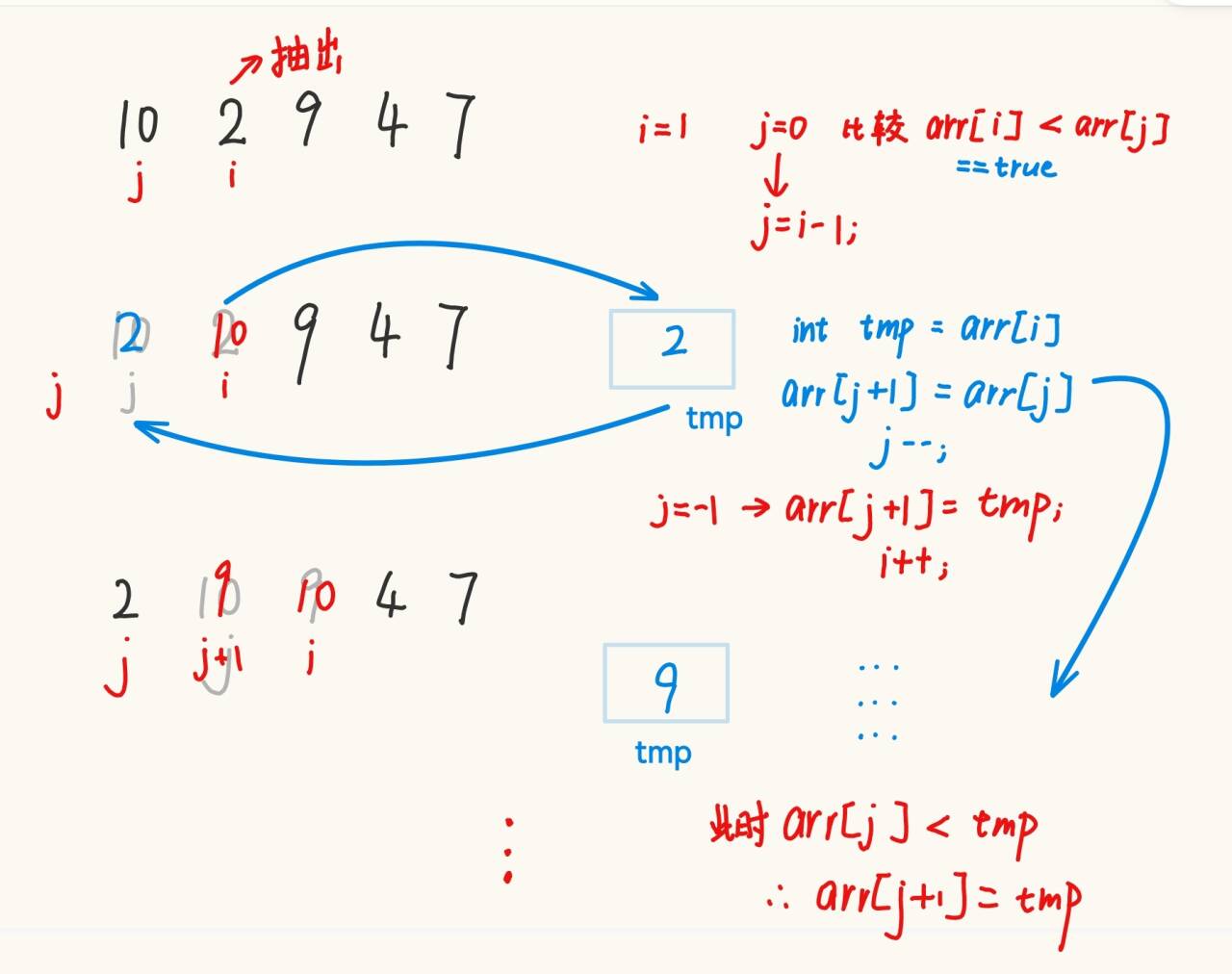
public class Sort {public static void insertSort(int[] array){for (int i = 1; i < array.length; i++) {int tmp = array[i];int j = i-1;for (; j >= 0; j--) {if (array[j] > tmp) {  // 若此處加了 = ，則得到的數據不穩定，但實際上直接插入排序法是穩定的array[j + 1] = array[j];}else{array[j + 1] = array[j];break;}}array[j+1] = tmp;}}
}

直接插入排序的特性：

1. 元素集合越接近有序，直接插入排序算法的時間效率越高，時間復雜度為O(N)；

2. 時間復雜度：最壞情況下是 O(N2)；

3. 空間復雜度：O(1)，沒有開辟空間；

4. 穩定性：穩定。

2.1.2 希爾排序（縮小增量排序）

? ? ? ? 基本思想：先選定一個整數作為增量，把待排序文件中的所有數據按照這個整數為距離分成多個組，即所有距離為增量的數據分在同一組內，將每一組的數據進行排序。然后，取另一個小于原來增量的整數（可以是原來的 1/2 或者 1/3+1），重復上述的分組和排序規則，當增量 =?1時，所有數據在同一組內排好序。是直接插入排序的優化，所以直接插入排序的代碼可以直接拿來修改。如下圖

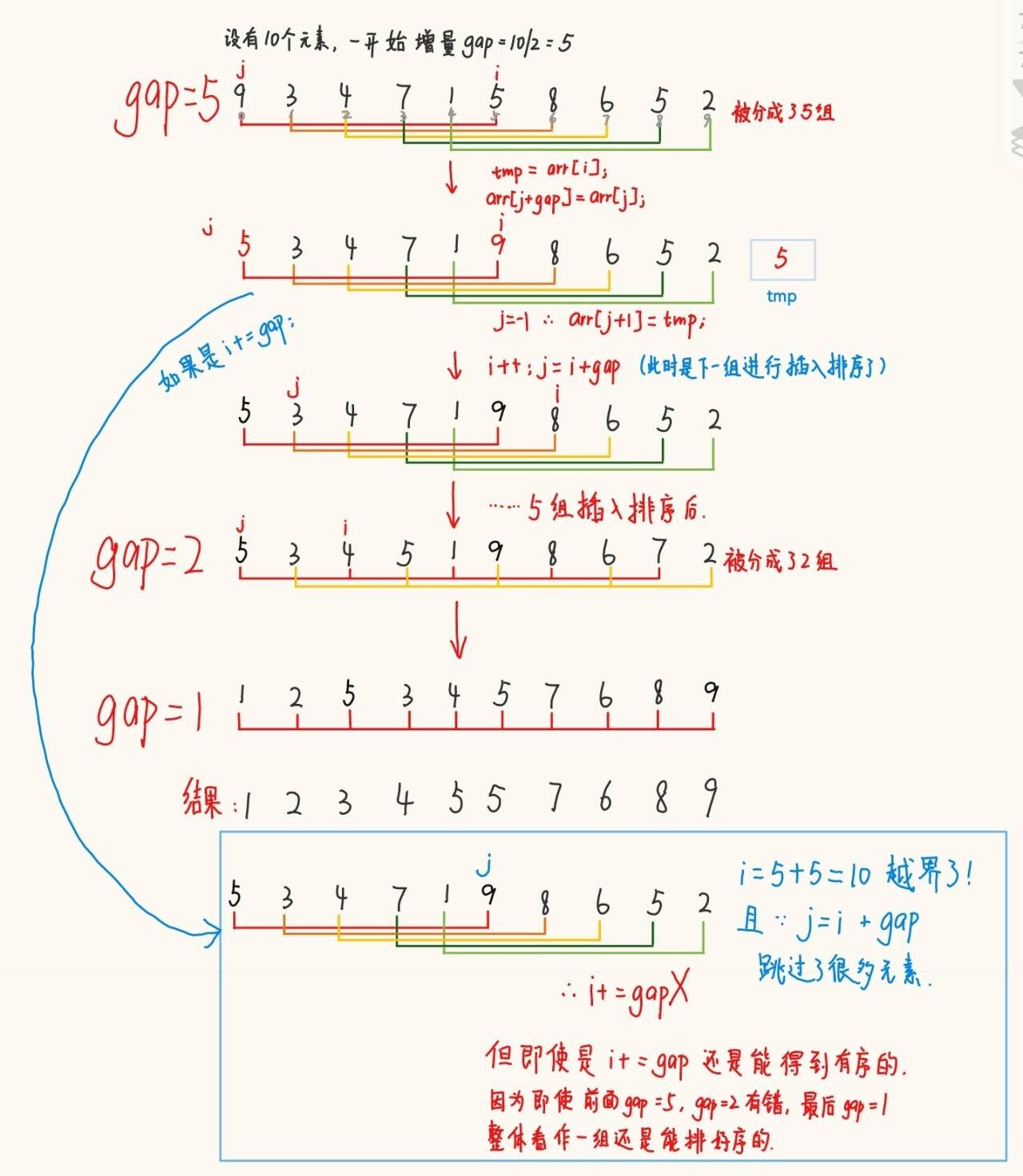
    public static void shellSort(int[] array){int gap = array.length;while (gap > 1){gap /= 2;  // 最后都能等于1shell(array, gap);}}private static void shell(int[] array, int gap) {for (int i = gap; i < array.length; i++) {int tmp = array[i];int j = i-gap;for (; j >= 0 ; j -= gap) {if (array[j] > tmp){array[j+gap] = array[j];}else{array[j+gap] = tmp;break;}}array[j+gap] = tmp;}}

希爾排序的特性：

1. 希爾排序是對直接插入排序的優化。

2. 當 gap > 1 時都是預排序，目的是讓數組更接近于有序。當 gap == 1 時，數組已經接近有序的了，這樣就會很快。這樣整體而言，可以達到優化的效果。我們實現后可以進行性能測試的對比。

3. 希爾排序的時間復雜度不好計算，因為gap的取值方法很多，導致很難去計算，因此在好些書中給出的希爾排、序的時間復雜度都不固定，歸納總結其時間復雜度的范圍在O(n^1.3 ~ n^1.5)之間；

4、空間復雜度：O(1)；

5、穩定性：不穩定。

????????性能測試：main() 方法中只有 testEfficiency() 測試數組是有序的或者無序時，各種排序方法的效率；而?testSimple() 則是查看是否排序成功。

package sort;import java.util.Arrays;
import java.util.Random;public class Test {public static void orderArray(int[] array){    // 初始化有序的數組for (int i = 0; i < array.length; i++) {// 順序array[i] = i;// 倒序//array[i] = array.length-1-i;}}public static void notOrderArray(int[] array){  // 初始化無序的數組Random random = new Random();for (int i = 0; i < array.length; i++) {array[i] = random.nextInt(10_0000);  // 生成0到10萬的隨機數}}public static void testInsertEfficiency(int[] array){array = Arrays.copyOf(array, array.length);     // 不改變原來數組的順序，而是將排序后的新的數組復制一份long startTime = System.currentTimeMillis();Sort.insertSort(array);long finishTime = System.currentTimeMillis();System.out.println("直接插入排序耗時："+(finishTime-startTime));}public static void testShellEfficiency(int[] array){array = Arrays.copyOf(array, array.length);     // 不改變原來數組的順序，而是將排序后的新的數組復制一份long startTime = System.currentTimeMillis();Sort.shellSort(array);long finishTime = System.currentTimeMillis();System.out.println("希爾排序耗時："+(finishTime-startTime));}public static void main(String[] args) {//testSimple();      // 測試例子給的數組testEfficiency();  // 測試耗時效率}public static void testSimple(){int[] array = {9,3,4,7,1,5,8,6,5,2};System.out.println("排序前："+Arrays.toString(array));Sort.shellSort(array);System.out.println("排序后："+Arrays.toString(array));}public static void testEfficiency(){int[] array = new int[10_0000];  // 數組元素個數為10萬orderArray(array);//notOrderArray(array);testInsertEfficiency(array);testShellEfficiency(array);}
}

????????對于有序的數組，直接插入排序耗時要比希爾排序短一點，但差不了多少，而如果是對無序的數組進行排序，希爾排序耗時要遠比直接插入排序耗時短，幾乎達到1：100。

2.2 選擇排序

????????基本思想：每一次從待排序的數據元素中選出最小（或最大）的一個元素，存放在序列的起始位置，直到全部待排序的數據元素排完。

2.2.1 直接選擇排序

假設0下標的元素為最小值，在后面的元素中找到實際最小值，然后交換……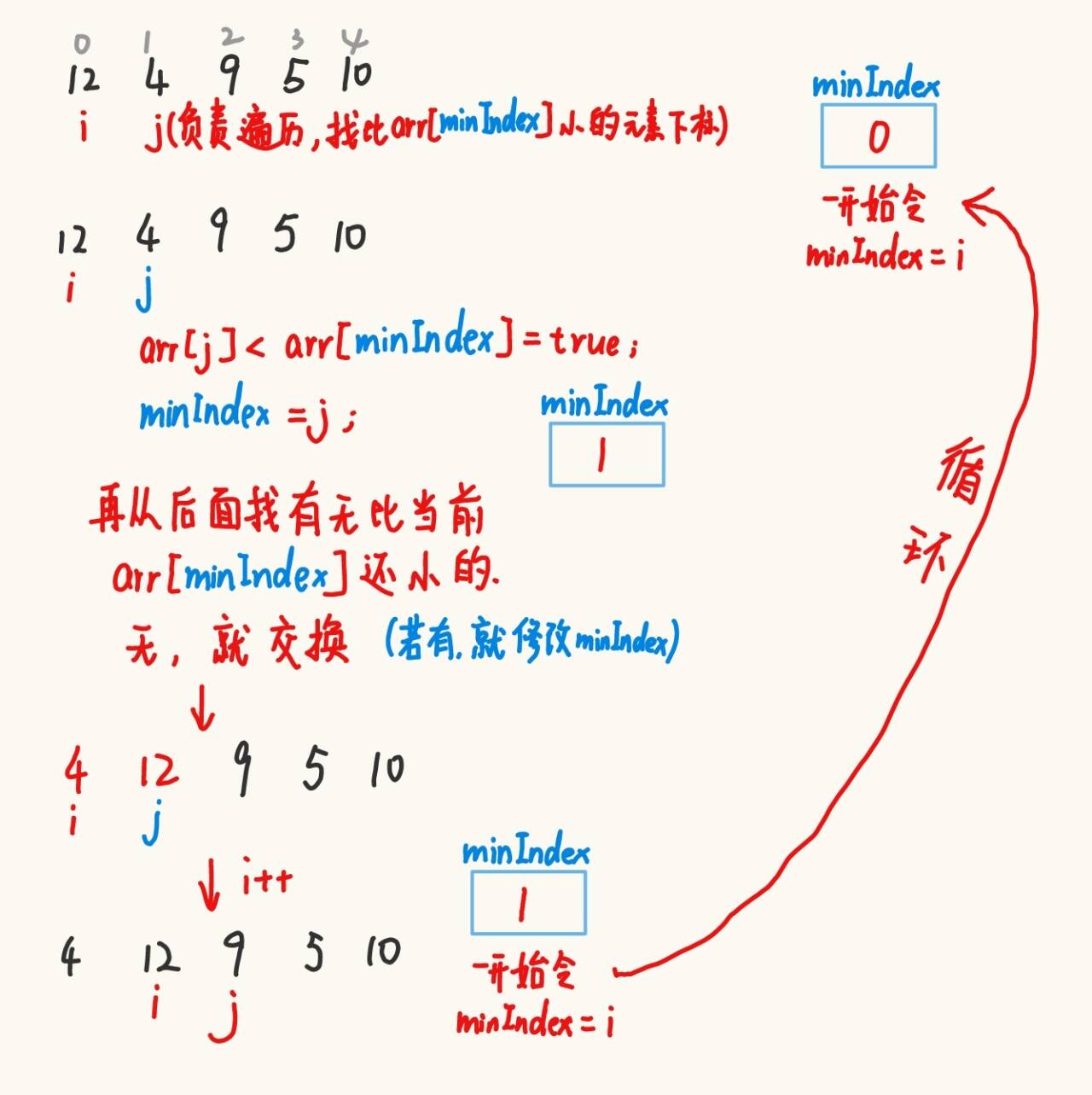

    public static void DirectSelectSort(int[] array){for (int i = 0; i < array.length; i++) {int minIndex = i;for (int j = i+1; j < array.length; j++) {if (array[j] < array[minIndex]){minIndex = j;}}swap(array, i, minIndex);}}private static void swap(int[] array, int i, int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}

直接選擇排序的特性：

1. 直接選擇排序思考非常好理解，但是效率不是很好。實際中很少使用，因此重要的是算法思想；
2. 時間復雜度：O(n2)，和數組是否有序無關
3. 空間復雜度：O(1)
4. 穩定性：不穩定

2.2.2 直接選擇排序優化

從左端點開始向右找到最小值將下標存到 minIndex 中，找到最大值并將下標存到 maxIndex 中。

上圖的步驟看似沒毛病，編寫代碼如下：

    public static void selectSort(int[] array){int left = 0;int right = array.length-1;while (left < right) {int minIndex = left;int maxIndex = left;for (int i = left+1; i <= right; i++) {if (array[i] > array[maxIndex]){maxIndex = i;}if (array[i] < array[minIndex]){minIndex = i;}}swap(array,left,minIndex);swap(array,right,maxIndex);left++;right--;}}

但是如果我們換一組數據進行測試，得到的結果如下：

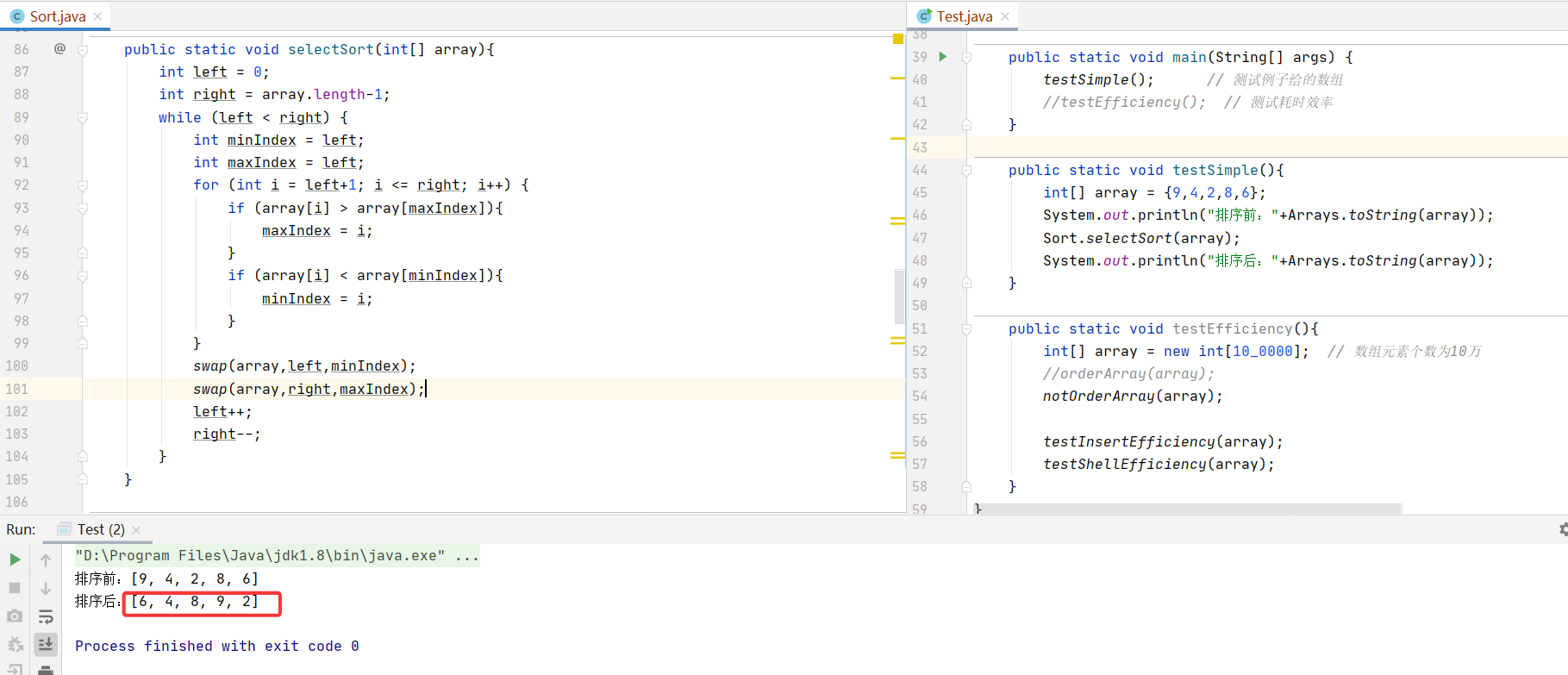
所以在更換完最小值之后需要增加一項條件。

    public static void selectSort(int[] array){int left = 0;int right = array.length-1;while (left < right) {int minIndex = left;int maxIndex = left;for (int i = left+1; i <= right; i++) {if (array[i] > array[maxIndex]){maxIndex = i;}if (array[i] < array[minIndex]){minIndex = i;}}swap(array,left,minIndex);// 如果最大值正好是 left 下標，那么交換 left 之后，最大值給到 minIndex 下標if (maxIndex == left){maxIndex = minIndex;}swap(array,right,maxIndex);left++;right--;}}

對于無序的數組，選擇排序的耗時如下：

2.2.3 堆排序

利用堆這種數據結構來實現排序，需要注意的是升序建大根堆，降序則是建小根堆。

我的Java集合中的優先級隊列（堆）中有提及。

    public static void heapSort(int[] array){createHeap(array);  // 1、建大根堆int end = array.length-1;while (end > 0){swap(array,0,end);  // 2、交換根節點和最后一個節點的值// 3、將除了最后一個元素（已是最大值）的其他節點重新整理成大根堆siftDown(array,0,end);end--;  // 4、倒著重復上面的操作}}public static void createHeap(int[] array){int parent = (array.length-1-1)/2;for (; parent >= 0; parent--) {siftDown(array,parent,array.length);}}private static void siftDown(int[] array, int parent, int size) {int child = 2*parent+1;while (child < size){if(child+1 < size && array[child+1] > array[child]){child++;}if (array[child] > array[parent]){swap(array,child,parent);parent = child;child = 2*parent+1;}else{break;}}}

堆排序的特性：

1. 堆排序使用堆來選數，效率就高了很多；

2. 時間復雜度：O(N*log?N) ，（目前效率最快的排序方法）

3. 空間復雜度：O(1)

4. 穩定性：不穩定

2.3 交換排序

????????基本思想：所謂交換，就是根據序列中兩個記錄鍵值的比較結果來對換這兩個記錄在序列中的位置，交換排序的特點是：將鍵值較大的記錄向序列的尾部移動，鍵值較小的記錄向序列的前部移動。

2.3.1 冒泡排序

關鍵詞：趟數、循環嵌套、j+1不要越界

    public static void bubbleSort(int[] array){for (int i = 0; i < array.length-1; i++) {boolean tag = false;for (int j = 0; j < array.length-1-i; j++) {if (array[j] > array[j+1]){swap(array,j, j+1);tag = true;}}if (!tag){break;}}}

1、時間復雜度 O(N2)

????????【一般討論沒有優化情況下的時間復雜度，即沒有boolean元素和 -i 的操作】

????????【優化之后，時間復雜度可以達到 O(N)】

2、空間復雜度 O(1)

3、穩定性：穩定

2.3.2 快速排序

????????快速排序是Hoare于1962年提出的一種二叉樹結構的基于分治法的交換排序方法，其基本思想為：
任取待排序元素序列中的某元素作為基準值，按照該排序碼將待排序集合分割成兩子序列，左子序列中所有元素均小于基準值，右子序列中所有元素均大于基準值，然后最左右子序列重復該過程，直到所有元素都排列在相應位置上為止。

    public static void quickSort(int[] array){quick(array,0,array.length-1);}public static void quick(int[] array, int start, int end){if (start >= end){  // 遞歸結束條件return;}//按照基準值對數組進行分割//int pivot = partitionHoare(array,start,end);          // Hoare//int pivot = partitionDig(array,start,end);            // 挖坑//int pivot =partitionDoublePointer(array,start,end);   // 雙指針解法1int pivot = partitionDoublePointer2(array,start,end);   // 雙指針解法2// 遞歸左邊的quick(array, start, pivot-1);// 遞歸右邊的quick(array,pivot+1,end);}

????????上述為快速排序遞歸實現的主框架，與二叉樹前序遍歷規則非常像，下面的3種分割方法都是在分割之后應用上面的遞歸方法進行排序的（如下圖右側內容），因此下面只討論不同分割方法的主要思想。

1、Hoare 法

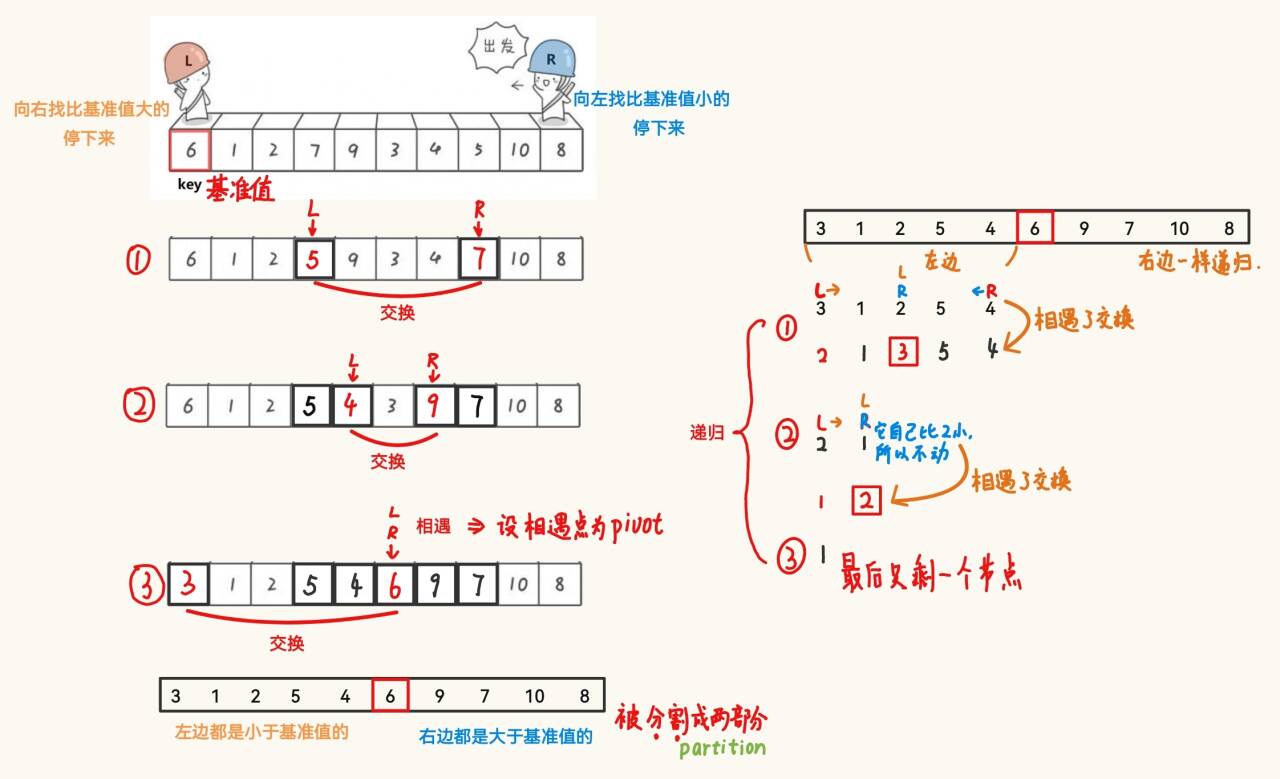
    public static void quickSort(int[] array){quick(array,0,array.length-1);}public static void quick(int[] array, int start, int end){if (start >= end){  // 遞歸結束條件return;}int pivot = partitionHoare(array,start,end);quick(array, start, pivot-1);quick(array,pivot+1,end);}private static int partitionHoare(int[] array, int left, int right){int tmp = array[left];int tmpIndex = left;while(left < right){while (left < right && array[right] >= tmp){right--;}while (left < right && array[left] <= tmp){left++;}swap(array, left, right);}swap(array,left,tmpIndex);return left;}

問題：畫圖理解 / 調試解決

????????1、為什么從后面開始找，而不是從前面開始找？

? ? ? ? 2、為什么在 while 條件中有等于號？

快排序的特性：

1、時間復雜度：

? ? ? ??最壞情況下：當給定數據是1 2 3 4 5 6…… / ……9 8 7 6 5 4 3 2 1這種有序的情況下，是O(N2）；

? ? ? ? 最好情況下：是 O(N*log?N)，對于滿二叉樹來說，對上面的代碼進行優化后可實現。

2、空間復雜度：遞歸一定會開辟內存

? ? ? ? 最壞情況下： O(N)，單分支二叉樹；

? ? ? ? 最好情況下： O(log?N)，對于滿二叉樹，遞歸完左邊再遞歸右邊時，左邊開辟的內存會被回收。

3、穩定性：不穩定

2、🔴挖坑法

如果在題目中遇到快速排序的結果，但沒有明確指出是哪種快排時，優先考慮挖坑法。

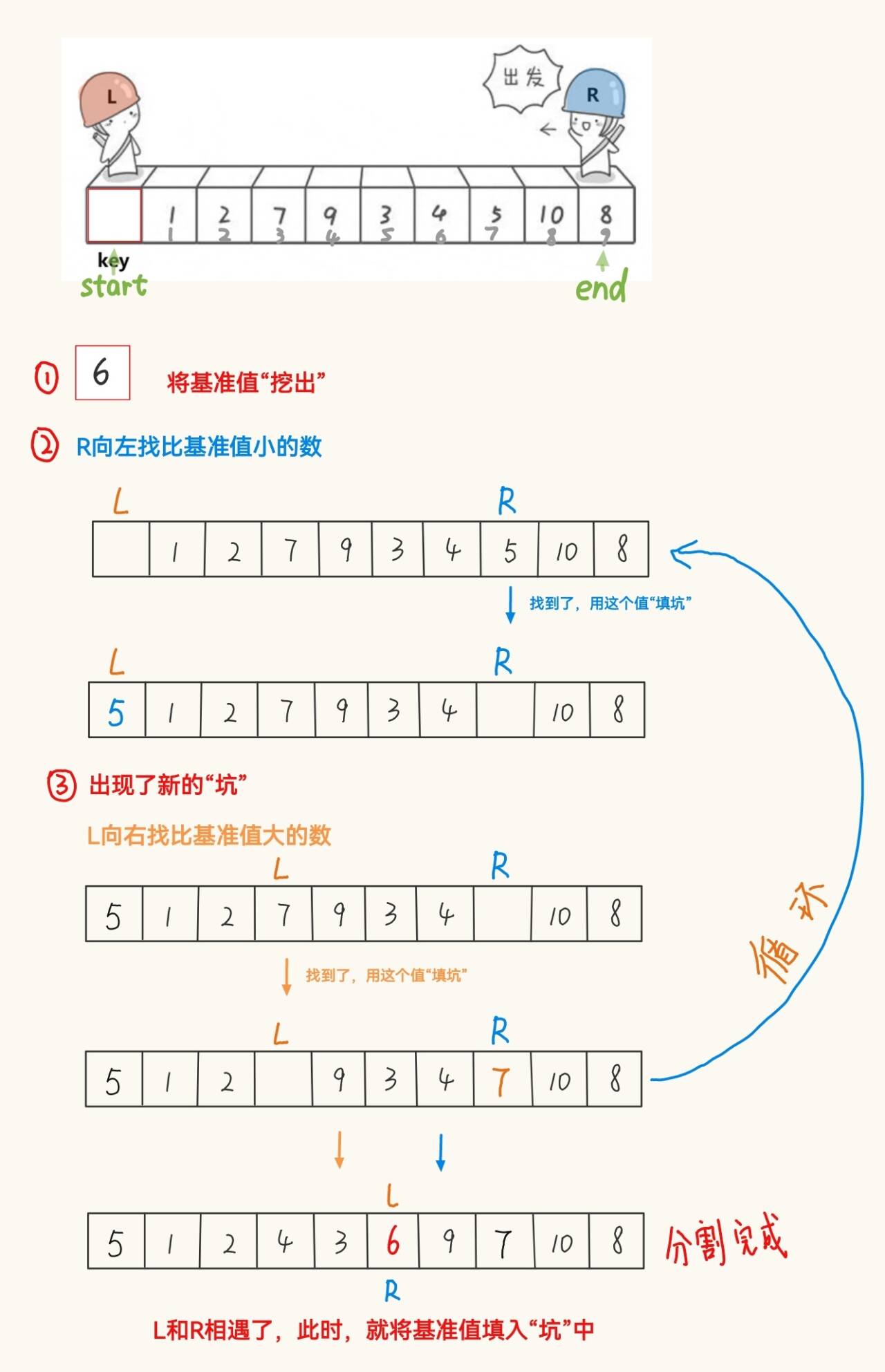
    public static void quickSort(int[] array){quick(array,0,array.length-1);}public static void quick(int[] array, int start, int end){if (start >= end){  // 遞歸結束條件return;}int pivot = partitionDig(array,start,end);quick(array, start, pivot-1);quick(array,pivot+1,end);}private static int partitionDig(int[] array, int left, int right){int key = array[left];while(left < right){while (left < right && array[right] >= key){right--;}array[left] = array[right];while (left < right && array[left] <= key){left++;}array[right] = array[left];}array[left] = key;return left;}

3、前后指針

兩種分割的方法：

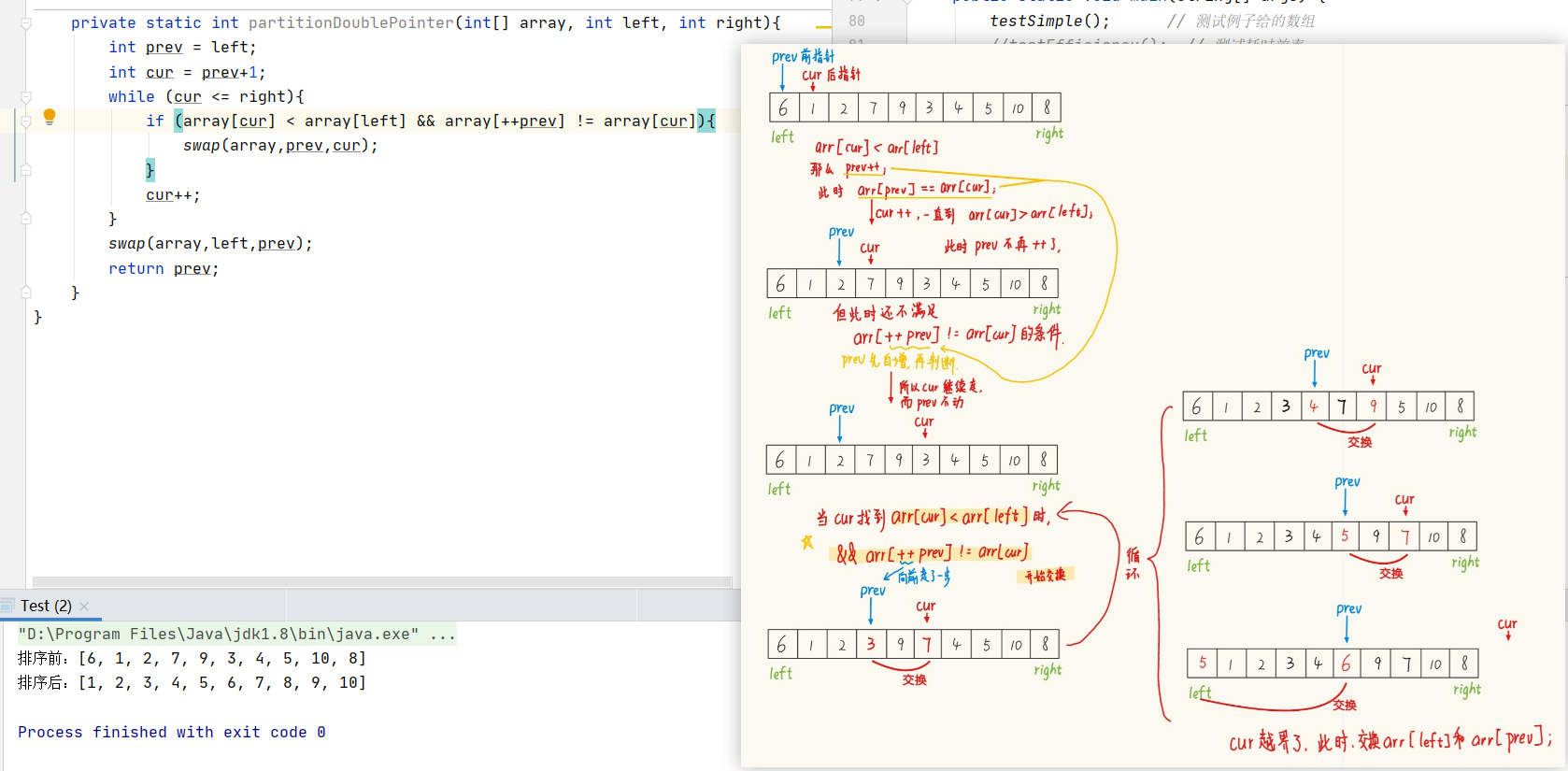
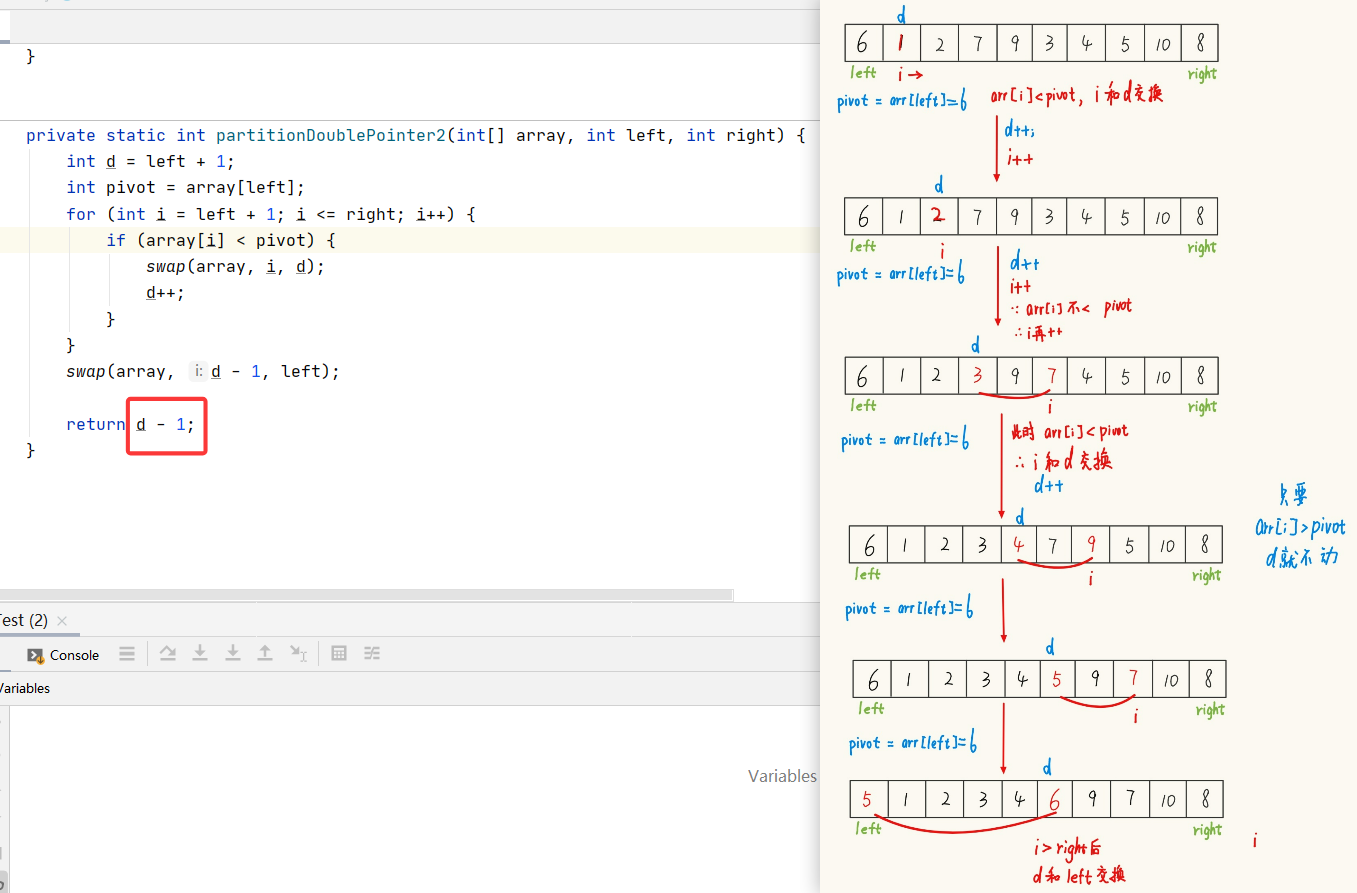
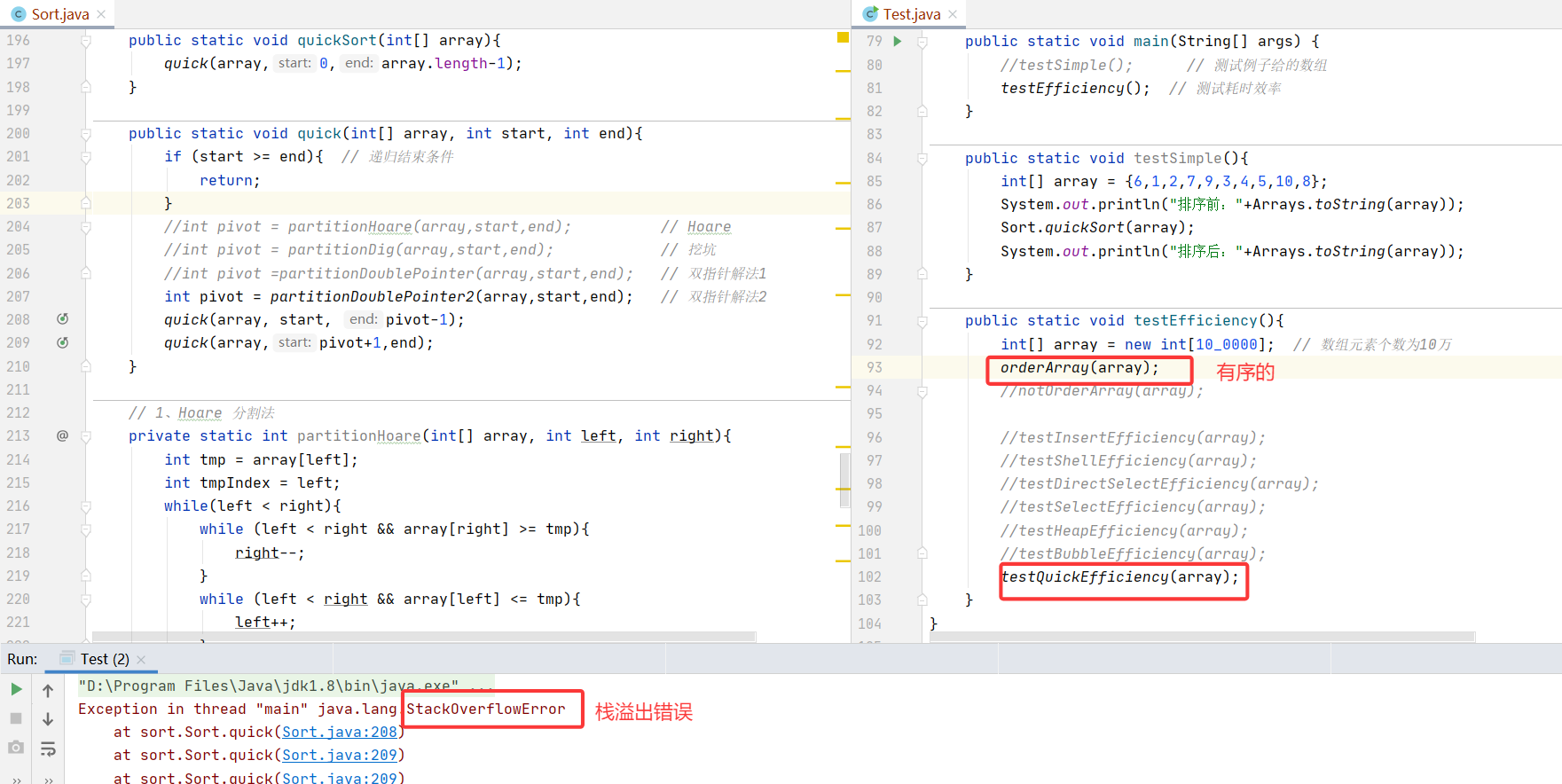
? ? ? ? 【對于有序的數組】當我們在測試快排序的效率時，程序崩潰了，這是因為遞歸需要開辟內存空間，對于十萬如此大量的且有序的數據就得開辟十萬個空間。而將數據量減小，比如1萬，并不會崩，但是效率還是比較低。

2.3.3 快速排序優化

1、三數取中法

在前面測試有序數組時程序崩潰了，這是因為遞歸有n個節點的單分支的二叉樹需要開辟n個內存，那么如果我們找到有序數組的中間值并將其作為分割的基準值，就能將有序數組分為兩部分。

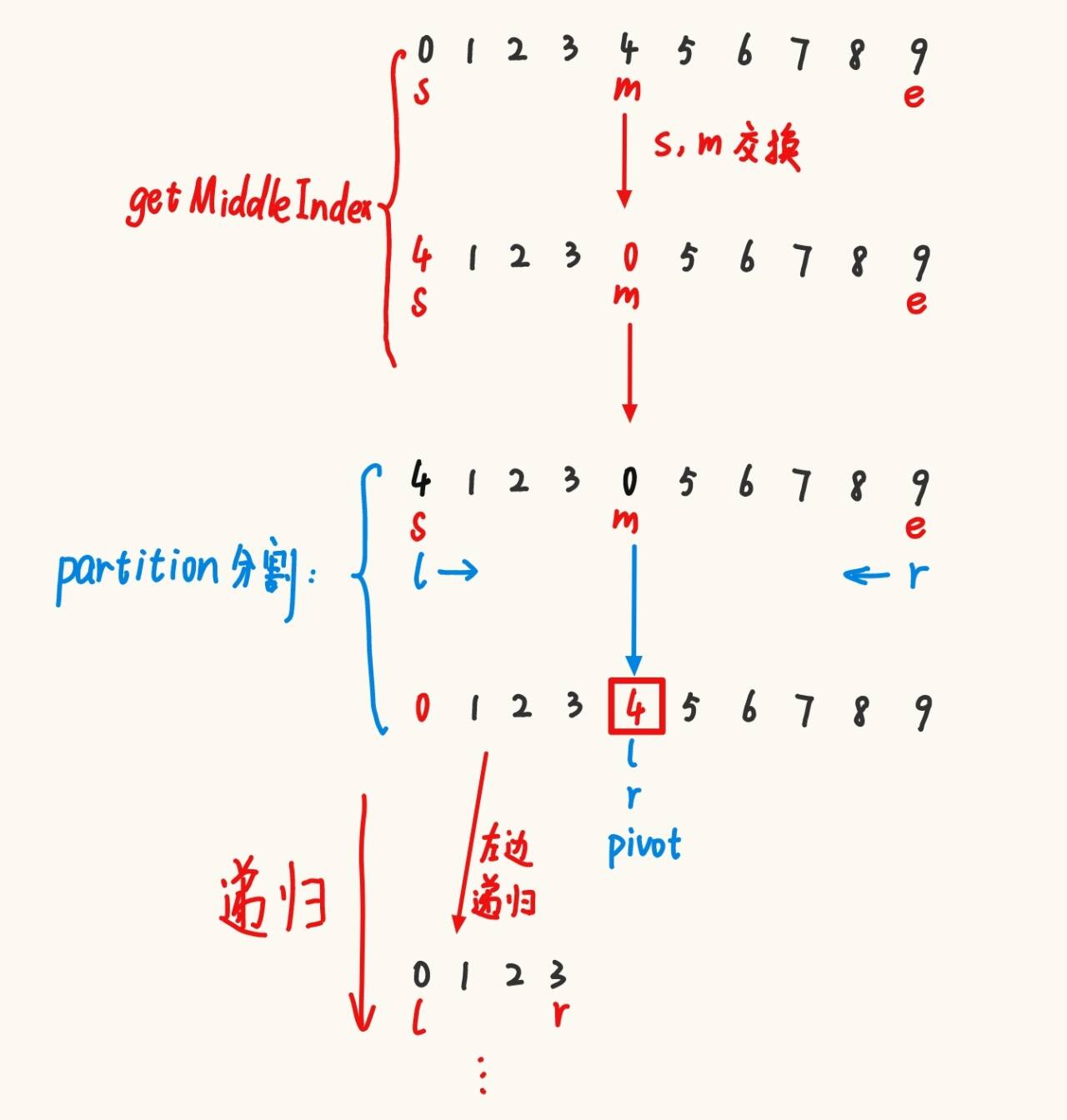
    public static void quick(int[] array, int start, int end){if (start >= end){  // 遞歸結束條件return;}// 三數取中法優化，有序的數組不再是單分支的二叉樹了//System.out.println("start: " + start + " end: " + end);  // 打印也會耗時int midIndex = getMiddleIndex(array, start, end);swap(array,start,midIndex);//int pivot = partitionHoare(array,start,end);          // Hoareint pivot = partitionDig(array,start,end);            // 挖坑//int pivot =partitionDoublePointer(array,start,end);   // 雙指針解法1//int pivot = partitionDoublePointer2(array,start,end);   // 雙指針解法2quick(array, start, pivot-1);quick(array,pivot+1,end);}private static int getMiddleIndex(int[] array, int start, int end) {int mid = (start+end)/2;if (array[start] < array[end]) {if (array[mid] < array[start]) {return start;} else if (array[mid] > array[end]) {return end;} else {return mid;}} else {if (array[mid] > array[start]) {return start;} else if (array[mid] < array[end]) {return end;} else {return mid;}}}

2、減少遞歸深度

????????因為在多次的預排序后數組已經趨于有序了，所以當遞歸到小的子區間時，可以考慮使用插入排序。

比如當數據量剩下的范圍是0到7之間時，直接使用插入排序，注意修改原來編寫的插入排序的開始和結束范圍，以及使用插入排序之后及時結束進程：

    public static void quick(int[] array, int start, int end){if (start >= end){  // 遞歸結束條件return;}// 減少遞歸深度優化if (end - start <= 7){insertSortRage(array, start, end);return;    // 記得此處要結束循環了}// 三數取中法優化，有序的數組不再是單分支的二叉樹了//System.out.println("start: " + start + " end: " + end);  // 打印也會耗時int midIndex = getMiddleIndex(array, start, end);swap(array,start,midIndex);//int pivot = partitionHoare(array,start,end);          // Hoareint pivot = partitionDig(array,start,end);            // 挖坑//int pivot =partitionDoublePointer(array,start,end);   // 雙指針解法1//int pivot = partitionDoublePointer2(array,start,end);   // 雙指針解法2quick(array, start, pivot-1);quick(array,pivot+1,end);}private static void insertSortRage(int[] array, int start, int end) {for (int i = start+1; i <= end; i++) {int tmp = array[i];int j = i-1;for (; j >= start; j--){if (array[j] > tmp){array[j+1] = array[j];}else{array[j+1] = tmp;break;}}array[j+1] = tmp;}}

2.3.4 快速排序非遞歸

????????基本思想：使用一個棧來存放分割后要使用二叉樹數據結構進行排序的開始下標和結束下標。再拿出下標進行分割，就是不斷地分割、存放下標、拿出下標、分割……的過程。

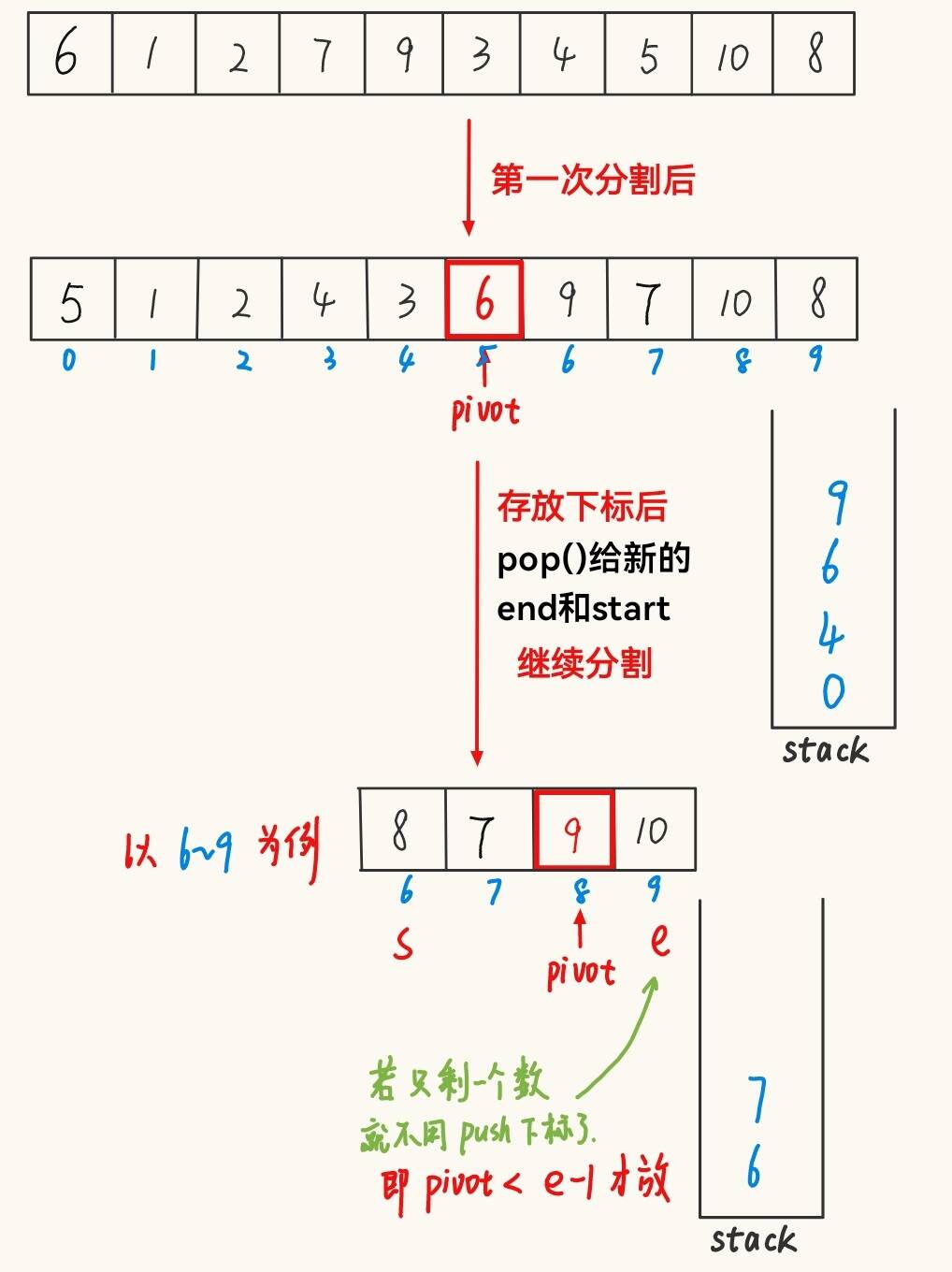
    public static void quickSort(int[] array){// 非遞歸的方法quickNor(array,0,array.length-1);}private static void quickNor(int[] array, int start, int end) {Deque<Integer> stack = new ArrayDeque<>();int pivot = partitionDig(array,start,end);// 第一次分割后存放下標if (pivot > start+1){stack.push(start);stack.push(pivot-1);}if (pivot < end-1){stack.push(pivot+1);stack.push(end);}// 拿出下標再進行分割while (!stack.isEmpty()){end = stack.pop();start = stack.pop();pivot = partitionDig(array,start,end);if (pivot > start+1){stack.push(start);stack.push(pivot-1);}if (pivot < end-1){stack.push(pivot+1);stack.push(end);}}}

快速排序的特性：

1、快速排序整體的綜合性能和使用場景都是比較好的，所以才敢叫快速排序；

2、時間復雜度：O(N*logN)；

3、空間復雜度：O(logN)，即樹的高度；

4. 穩定性：不穩定。

2.4 歸并排序

2.4.1?

????????基本思想：歸并排序（MERGE-SORT）是建立在歸并操作上的一種有效的排序算法,該算法是采用分治法（Divide and Conquer）的一個非常典型的應用。將已有序的子序列合并，得到完全有序的序列；即先使每個子序列有序，再使子序列段間有序。若將兩個有序表合并成一個有序表，稱為二路歸并。歸并排序核心步驟：

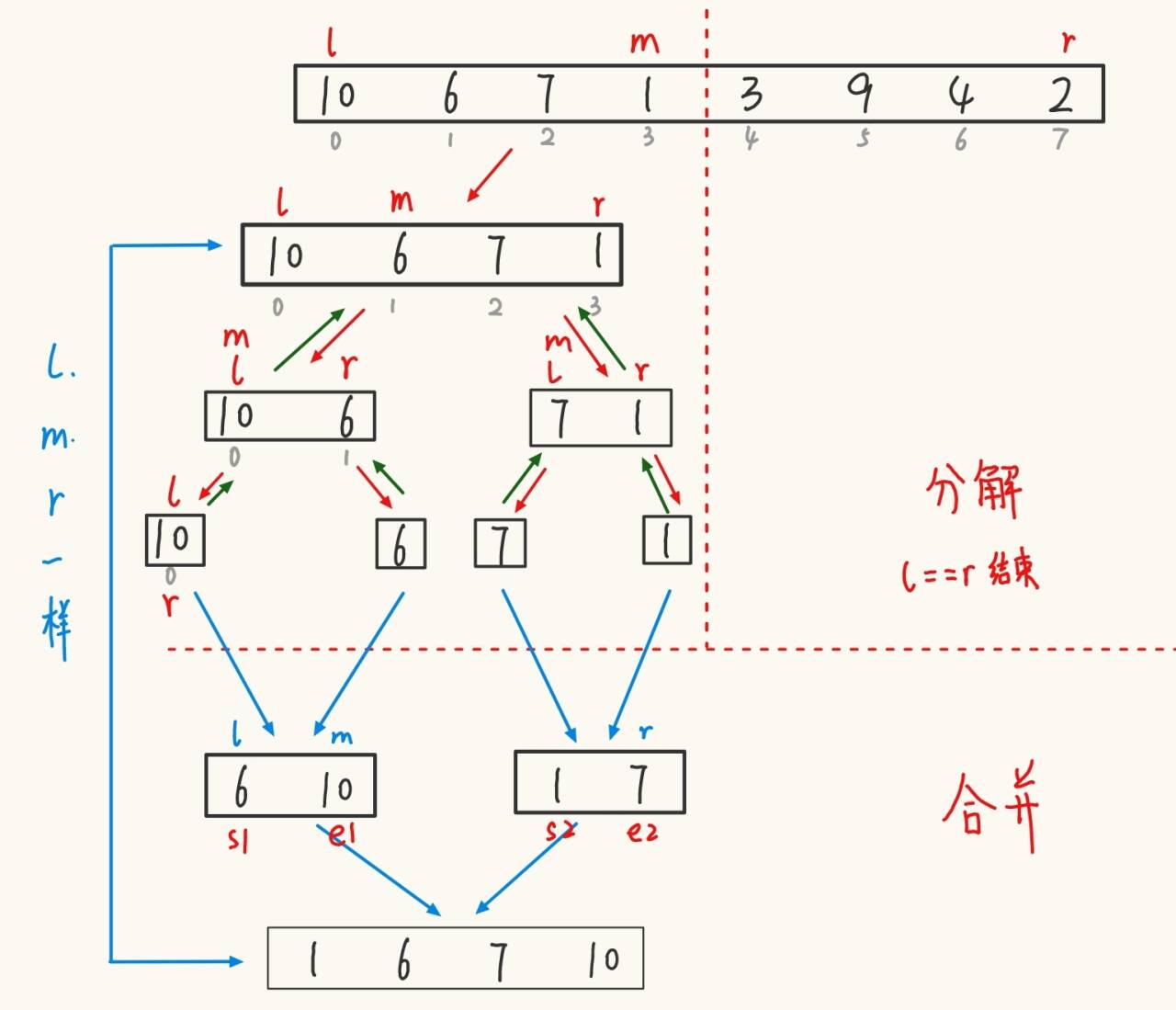
    public static void mergeSort(int[] array){mergeSortTmp(array, 0, array.length-1);}public static void mergeSortTmp(int[] array, int left, int right){if (left >= right){return;}int mid = (left + right)/2;mergeSortTmp(array, left, mid);mergeSortTmp(array, mid+1, right);// 到這里分解結束// 下面進行合并merge(array,left,mid,right);}private static void merge(int[] array, int left, int mid, int right) {int[] tmp = new int[right-left+1];int k = 0;int s1 = left;//int e1 = mid;int s2 = mid+1;//int e2 = right;while (s1 <= mid && s2 <= right){if (array[s1] < array[s2]){tmp[k++] = array[s1++];}else{tmp[k++] = array[s2++];}}while (s1 <= mid){   // 要用 while 的原因是有可能有多組tmp[k++] = array[s1++];}while (s2 <= right){tmp[k++] = array[s2++];}for (int i = 0; i < k; i++) {array[i+left] = tmp[i];  // +left處理巧妙解決右邊下標對應問題}}

歸并排序特性：

1、歸并的缺點在于需要O(N)的空間復雜度，歸并排序的思考更多的是解決在磁盤中的外部排序問題；

2、時間復雜度：O(N*log?N)；

3、空間復雜度：O(N)

4、穩定性：穩定

海量數據的排序問題：

外部排序：排序過程需要在磁盤等外部存儲進行的排序

前提：內存只有 1G，需要排序的數據有 100G

????????因為內存中因為無法把所有數據全部放下，所以需要外部排序，而歸并排序是最常用的外部排序

1. 先把文件切分成 200 份，每個 512 M

2. 分別對 512 M 排序，因為內存已經可以放的下，所以任意排序方式都可以

3. 進行 2路歸并，同時對 200 份有序文件做歸并過程，最終結果就有序了

2.4.2 歸并排序非遞歸實現

????????基本思想：將數組多次分解之后合并為一整個數組進行排序。

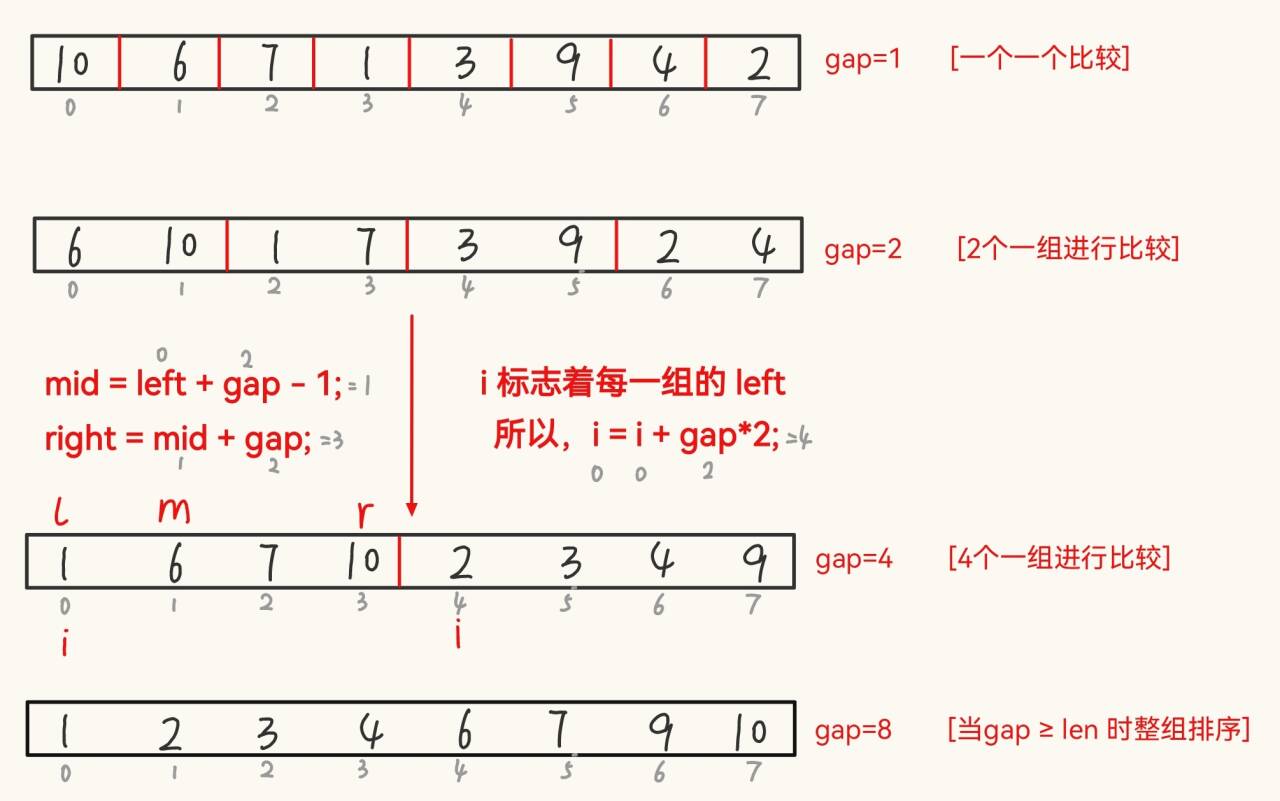
    private static void merge(int[] array, int left, int mid, int right) {  // 合并int[] tmp = new int[right-left+1];int k = 0;int s1 = left;//int e1 = mid;int s2 = mid+1;//int e2 = right;while (s1 <= mid && s2 <= right){if (array[s1] < array[s2]){tmp[k++] = array[s1++];}else{tmp[k++] = array[s2++];}}while (s1 <= mid){   // 要用 while 的原因是有可能有多組tmp[k++] = array[s1++];}while (s2 <= right){tmp[k++] = array[s2++];}for (int i = 0; i < k; i++) {array[i+left] = tmp[i];}}// 歸并排序非遞歸public static void mergeSortNor(int[] array){int gap = 1;while (gap < array.length) {for (int i = 0; i < array.length; i = i + gap * 2) {int left = i;int mid = left + gap - 1;int right = mid + gap;merge(array, left, mid, right);  // 合并}gap *= 2;}}

上面的 mergeSortNor() 代碼看似沒有問題，但是如果是如下情況，該如何完善？

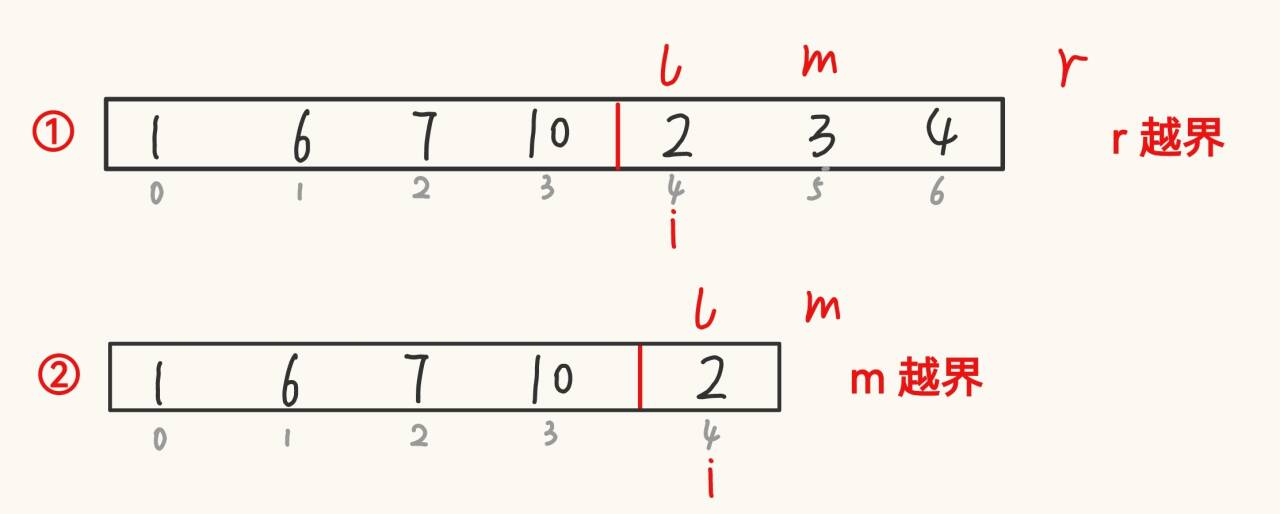
    public static void mergeSortNor(int[] array){int gap = 1;while (gap < array.length) {for (int i = 0; i < array.length; i = i + gap * 2) {int left = i;int mid = left + gap - 1;if (mid >= array.length){  // 處理越界情況mid = array.length -1;}int right = mid + gap;if (right >= array.length){right = array.length -1;}merge(array, left, mid, right);  // 合并}gap *= 2;}}

三、特性總結

堆排序、快速排序、歸并排序時間復雜度都是 O(N*log?N)；但相比空間復雜度，堆排序占優勢

插入排序、冒泡排序和歸并排序都是穩定的；

排序方法	最好	平均	最壞	空間復雜度	穩定性
冒泡排序	O(n2)（優化之后能達到O(n)）	O(n2)	O(n2)	O(1)	穩定
插入排序	O(n)	O(n2)	O(n2)	O(1)	穩定
選擇排序	O(n2)	O(n2)	O(n2)	O(1)	不穩定
希爾排序	O(n)	O(n^1.3)	O(n^1.5)	O(1)	不穩定
堆排序	O(n * log?n)	O(n * log?n)	O(n * log?n)	O(1)	不穩定
快速排序	O(n * log?n)	O(n * log?n)	O(n2)	O(log?n)~O(n)	不穩定
歸并排序	O(n * log?n)	O(n * log?n)	O(n * log?n)	O(n)	穩定

一些操作關鍵詞：

四、其他非基于比較排序

4.1 計數排序

應用場景：

????????集中在某個范圍內的一組數據。

操作步驟：

????????1、新建一個計數數組來利用下標統計相同元素出現的次數；

????????2、根據統計的結果將序列回收到原來的序列中。

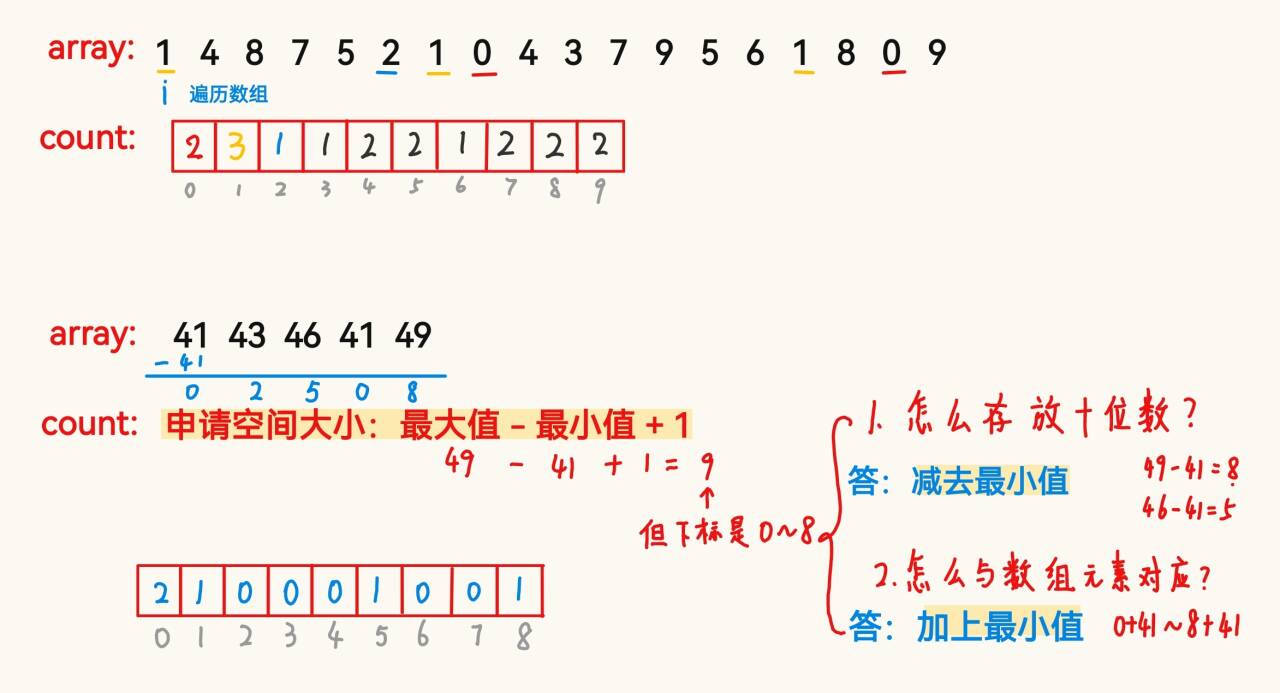
    public static void countSort(int[] array){// 1、找出數組中的最大值和最小值，得到申請空間的大小int max = array[0];int min = array[0];for (int i = 1; i < array.length; i++) {if (array[i] > max){max = array[i];}if (array[i] < min){min = array[i];}}int len = max - min + 1;int[] count = new int[len];// 2、遍歷數組計算出現的次數for (int i = 0; i < array.length; i++) {int index = array[i];count[index-min]++;}// 3、將計數數組中的數據按順序拿出放到 arrayint index = 0;for (int i = 0; i < count.length; i++) {while (count[i] != 0) {array[index] = i + min;index++;count[i]--;}}}

計數排序的特性：