（數據科學學習手札30）樸素貝葉斯分類器的原理詳解Python與R實現

一、簡介

　　要介紹樸素貝葉斯（naive bayes）分類器，就不得不先介紹貝葉斯決策論的相關理論：

　　貝葉斯決策論（bayesian decision theory）是概率框架下實施決策的基本方法。對分類任務來說，在所有相關概率都已知的理想情況下，貝葉斯決策論考慮如何基于這些概率和誤判損失來選擇最優的類別標記結果。

二、貝葉斯決策論的基本原理

　　我們以多分類任務為例：

　　假設有N種可能的類別標記，即y={c₁,c₂,...,c_N}，λ_ij是將一個真實類別為c_j的樣本誤分類為c_i的損失，基于后驗概率P(c_i|c_j)可獲得將樣本x分類為c_i所產生的期望損失（expected loss），即在樣本x上的“條件風險”（conditional risk）

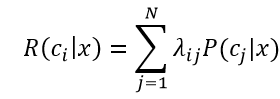
　　我們的目的是尋得一個判定準則h：X-->Y，以最小化總體風險：

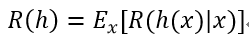
　　對每一個樣本x，若h能最小化條件風險

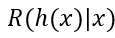
則總體風險R(h)也將被最小化，這就產生了貝葉斯判定準則（Bayes decision rule）：為最小化總體風險，只需要在每個樣本上選擇能使條件風險R(c|x)最小的類別標記，即

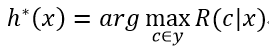
h*被稱作貝葉斯最優分類器（Bayes optimal classifier），與之對應的總體風險R(h*)稱為貝葉斯風險（Bayes risk）。1-R(h*)反映了分類器所能達到的最佳性能，即通過機器學習所能達到的模型精度的理論上限。

　　若目標是最小化分類錯誤率，則誤判損失λ_ij可寫作

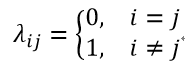
此時的條件風險

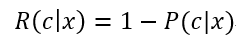
于是，最小化分類錯誤率的貝葉斯最優分類器為：

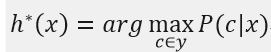
　　即對每個樣本x，選擇使得后驗概率P(c|x)最大的類別標記，所以利用貝葉斯判定準則來最小化決策風險的首要工作是求得后驗概率P(c|x)，這在現實任務中通常難以直接獲得，而機器學習所要實現的是基于有限的訓練樣本集來盡可能準確地估計后驗概率，主要有兩種策略：

　　1、“判定式模型”（discriminative model）

　　給定x，通過直接對P(c|x)建模來預測c；

　　2、“生成式模型”（generative model）

　　對聯合概率分布P(x,c)建模，然后再由此獲得P(c|x)；

貝葉斯分類器便是一種生成式模型，對生成式模型，考慮條件概率公式：

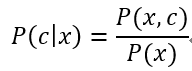
基于貝葉斯定理，P(c|x)可寫為：

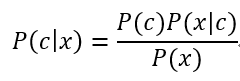
其中，P(c)是類先驗概率（prior）；P(x|c)是樣本x對應類別c的類條件概率（class-condtional probability），或稱為“似然”（likelihood）；P(x)是用于歸一化的“證據”（evidence）因子。對給定樣本x，證據因子P(x)與類別無關，因此估計P(c|x)的問題就轉化為如何基于訓練數據D來估計P(c)和似然P(x|c)，類先驗概率P(c)表達了樣本空間中各類樣本所占的比例，根據大數定律，當樣本數據規模足夠大時，就可以用樣本數據的各類別出現的頻率來估計P(c)。

　　上述過程雖然看起來很簡單，但是應用到現實任務中就會遇到很多局限，對類條件概率P(x|c)，由于它涉及所有關于x的屬性的聯合概率，直接根據樣本出現的頻率來估計將會遇到困難，因為實際任務中的訓練樣本集是有限的，而要估計聯合分布就需要獲得各種可能狀態的樣本，這顯然無法辦到，因為自變量各個維度上的組合方式是指數式增長的，遠遠大于樣本數量，導致很多可能的樣本取值從未在訓練集中出現過，所以直接用頻率來估計P(x|c)不可行，因為這樣會直接把未出現過與概率為0畫上等號。

　　為了克服貝葉斯分類器中的局限，我們基于更寬松的理論條件構建出樸素貝葉斯分類器；

三、樸素貝葉斯分類器

　　為了避開貝葉斯公式的訓練障礙，樸素貝葉斯分類器采用了“屬性條件獨立性假設”（attribute conditional independence assumption），即對已知類別，假設所有屬性相互獨立，即每個屬性各自獨立地對分類結果產生影響，則我們前面提到的貝葉斯公式：

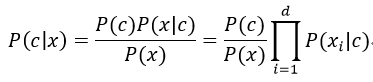
其中d表示屬性的個數，x_i表示x在第i個屬性上的取值，又因為P(x)由樣本集唯一確定，即對所有類別P(x)都相同，于是樸素貝葉斯分類器的表達式：

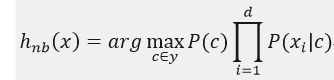
　　樸素貝葉斯分類器的訓練過程就是基于訓練集D來估計類先驗概率P(c)，并為每個屬性估計條件概率P(x_i|c)，用D_c表示訓練集D中第c類樣本組成的集合，若有充足的獨立同分布樣本，則可以容易地估計出類先驗概率：

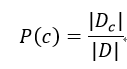
對離散屬性而言，令D_c,xi表示D_c中在第i個屬性上取值為x_i的樣本組成的集合，則條件概率P(x_i|c)為：

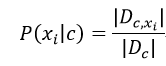
　　對連續型屬性，假定：

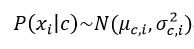
其中μ_c,i，σ²_c,i分別為第c類樣本在屬性i上的均值與方差（這里要假設對應的連續型變量服從正態分布），則：

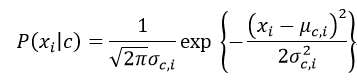
　　下面以一個簡單的例子來詳細說明這個過程：

　　對給定的訓練集D，以類別c{c=1/0}作為分類目標，對所有在訓練集出現過的屬性x_i屬于X，依此進行下列計算（估計）：

　　1、類先驗概率P(c)

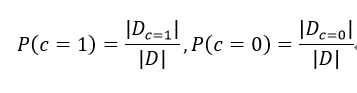
　　2、各屬性的條件概率

　　以x₁為例：

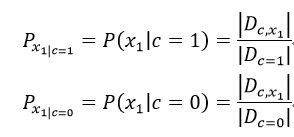
　　若x_i為連續型變量，則利用不同類別中該屬性的樣本均值與樣本方差來估計真實的不同類別中該屬性的正態分布對應的參數，求出對應的密度函數；計算出所有屬性對所有可能的類別的條件概率；

　　3、對樣本進行分類

　　針對我們所舉的例子，有如下兩種情況：

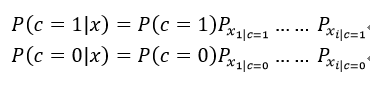
取其中結果較大者對應類別作為最終對樣本的分類結果。

修正情況：

　　有些時候，若某個屬性值在訓練集中沒有與某個類同時出現過，則直接使用上述過程估計后驗概率會將整個結果拖累至0，因此這種情況下我們進行如下處理：

平滑（smoothing）

　　為了避免上面描述的，樣本的其他屬性攜帶的信息被訓練集中未出現過的屬性抹去，則在估計概率值的時候要進行“平滑”處理，常用“拉普拉斯修正”（Laplacian correction），具體操作如下：

　　我們用N表示訓練集D中可能的類別數，N_i表示第i個屬性可能的取值個數，則：

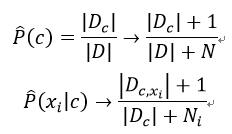
這種修正方法避免了因訓練集樣本不充分而導致概率估值為0的問題，并且在訓練集變大時，修正過程所引入的先驗（prior）的影響也會逐漸變得可以忽略，使得估值漸漸趨向于實際概率值。

現實中的使用方式：

　　1、任務對預測速度要求較高時

　　可以事先將樣本中所有先驗概率和類條件概率計算好并儲存起來，等到需要預測新樣本類別時查表計算對應的后驗概率即可；

　　2、任務數據更替頻繁時

　　可采用“懶惰學習”（lazy learning）的方式，先不進行任何事先訓練，僅在有預測需求時才根據當前樣本進行概率估計與預測；

　　3、數據不斷增加時

　　若數據不斷增加，則可在現有概率估值的基礎上，僅對新增樣本的屬性值所涉及的概率估值進行修正即可實現增量學習（在線學習）；

四、Python實現

　　我們使用sklearn.naive_bayes中的GaussianNB()來進行樸素貝葉斯分類，這種方法基于的就是我們前面提到的假設非類別型的連續數值變量服從正態分布即高斯分布，其參數非常簡單（因為整個建模過程沒有什么需要調參數的地方）如下：

priors：數組型，控制針對各類別比例的先驗分布，若本參數有輸入，則接下來的先驗分布將不再基于樣本集進行計算；

函數輸出項：

class_prior_：輸出基于樣本集計算出的各類別的先驗分布

class_count_：輸出訓練集中各個類別的樣本數量

theta_：輸出計算出的對應各連續型特征各類別的樣本均值

sigma_：輸出計算出的對應各連續型特征各類別的樣本方差

下面以我們喜聞樂見的鳶尾花數據進行演示：

from sklearn.naive_bayes import GaussianNB
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.metrics import confusion_matrix'''載入數據'''
X,y = datasets.load_iris(return_X_y=True)'''分割訓練集與驗證集，這里采用分層抽樣的方法控制類別的先驗概率'''
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,stratify=y)'''初始化高斯樸素貝葉斯分類器'''
clf = GaussianNB()'''訓練分類器'''
clf = clf.fit(X_train,y_train)'''打印分類器在驗證集上的混淆矩陣'''
print('混淆矩陣：')
print(confusion_matrix(y_test,clf.predict(X_test)))'''打印測試集上的正確率'''
print('測試集正確率：'+str(clf.score(X_test,y_test)))'''打印分類器訓練后的各返回項'''
print('類別的先驗分布：',clf.class_prior_)print('各類別樣本數量：',clf.class_count_)print('各類別對應各連續屬性的正態分布的均值：','\n',clf.theta_)print('各類別對應各連續屬性的正態分布的方差：','\n',clf.sigma_)

運行結果：

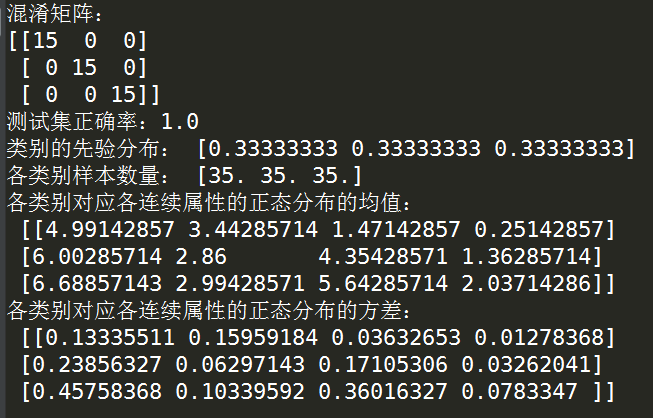
五、R實現

　　在R中有很多包支持樸素貝葉斯分類（事實上自己寫自編函數實現也不是件難事），這里選用比較有代表性的e1071包中的naiveBayes()來完成相應功能，其主要參數如下：

formula：這時R中常見的一種格式，類別標簽~自變量的輸入形式

data：指定訓練數據所在的數據框

laplace：控制前面提到的平滑處理中的拉普拉斯修正，默認值為0，即不進行平滑，若需要進行拉普拉斯修正，這里建議值為1

下面是一個簡單的演示：

> rm(list=ls())
> library(e1071)
> data(iris)
> 
> #留出法分割訓練集與驗證集
> sam <- sample(1:dim(iris)[1],dim(iris)[1]*0.8)
> X_train <- iris[sam,1:4]
> y_train <- iris[sam,5]
> X_test <- iris[-sam,1:4]
> y_test <- iris[-sam,5]
> train <- cbind(y_train,X_train)
> 
> #利用訓練集訓練樸素貝葉斯分類器
> clf <- naiveBayes(y_train~.,data=train)
> 
> #混淆矩陣
> table(y_test,predict(clf,X_test))y_test       setosa versicolor virginicasetosa          9          0         0versicolor      0          7         1virginica       0          0        13
> 
> #測試正確率
> sum(diag(prop.table(table(y_test,predict(clf,X_test)))))
[1] 0.9666667