機器學習-SVM（支持向量機）

推薦課程：【機器學習實戰】第5期支持向量機 |數據分析|機器學習|算法|菊安醬_嗶哩嗶哩_bilibili

贊美菊神ヾ ( ゜ⅴ゜)ﾉ?

一、什么是支持向量機？

支持向量機（Support Vector Machine, SVM）是一類按監督學習（supervised learning）方式對數據進行二元分類的廣義線性分類器（generalized linear classifier），其決策邊界是對學習樣本求解的最大邊距超平面（maximum-margin hyperplane）。

1.1?舉個例子?

在桌子上似乎有規律地放了兩種顏色的球，要求你用一根棍子分離開他們，并且盡量再放更多的球之后，仍然適用。

SVM就是試圖把棍放在最佳位置，好讓在棍的兩邊有盡可能大的間隙（這被認為是最佳求解）。?

并且，現在即使再放入更多的球，棍子仍然是一個很好的分界線。

但是，現在增加難度，如果將球散亂地放在桌子上，又該怎樣進行劃分呢？很明顯，此時在二維平面中，這變成了一個線性不可分的問題，我們沒有方法再用一根棍子將這些球分開了，那么怎么解決這樣一個問題呢？

解決方法也很簡單，我們可以使用一個核函數，將二維平面中的 '小球' 投影到三維空間，也許就可以在三維空間中，有可能找到這樣一個平面將其分隔開來。（可以想象一下，用力拍向桌子，然后桌子上的球就被震到空中，瞬間抓起一張紙，插到兩種球的中間。）

（話說，如果3維空間依舊找不到這樣一個平面呢？沒關系，我繼續投四維呀╮(??? ????)╭，總能找到一個維度解決線性不可分的問題。）

可以通過視頻，更為直觀地感受一下這個過程：支持向量機 SVM在線性不可分情況下進行分類可視化直觀展示高維空間映射_嗶哩嗶哩_bilibili

而在二維平面的角度看這些球，這些球像是被一條曲線分開了。

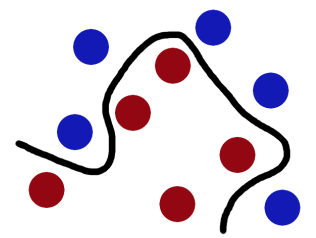
更為規范的，我們把這些球叫做「data」，把棍子叫做「classififier」, 最大間隙 trick 叫做「optimization」，拍桌子叫做「kernelling」, 那張紙叫做「hyperplane」。

? ??

1.2?概述一下

當一個分類問題，數據是線性可分（linearly separable）的，也就是用一根棍就可以將兩種小球分開的時候，我們只要將棍的位置放在讓小球距離棍的距離最大化的位置即可，尋找這個最大間隔的過程，就叫做最優化。但是，一般的數據是線性不可分的，也就是找不到一個棍將兩種小球很好的類。這個時候，我們就需要使用核函數?（kernel）將小球投影到多維空間（想象一下，將小球拍飛到空中，瞬間抓起一張紙，插到兩種球的中間），而在多維空間中切分小球的平面，就是超平面（hyperplane）。如果數據集是N維的，那么超平面就是N-1維的。

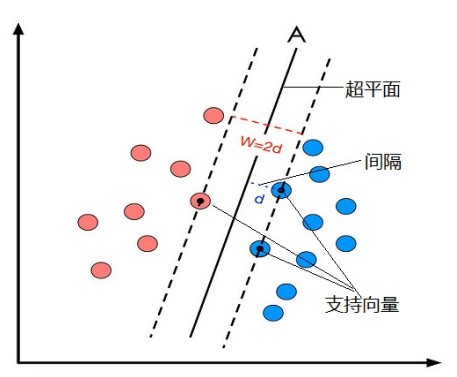
Q：什么是支持向量？

A：把一個數據集正確分開的超平面可能有多個，而那個具有“最大間隔”的超平面就是SVM要尋找的最優解。而這個真正的最優解對應的兩側虛線所穿過的樣本點，就是SVM中的支持樣本點，稱為“支持向量（support vector）”。支持向量到超平面的距離被稱為間隔（margin）。?

? ??

二、線性支持向量機

一個最優化問題通常有兩個最基本的因素：

1）目標函數，也就是你希望什么東西的什么指標達到最好；

2）優化對象，你期望通過改變哪些因素來使你的目標函數達到最優。

在線性SVM算法中，目標函數顯然就是那個“間隔”，而優化對象則是超平面。

2.1?超平面方程

在線性可分的二分類問題中，超平面其實就是一條直線，公式如下：

將原來的x軸看作x1軸，y軸看作x2軸，于是公式(1)轉換為：

向量形式可以寫成：

進一步可表示為：

其中，，b為截距。

? ?

2.2?間隔的計算公式?

間隔的計算公式 = 點到直線距離推導公式，向量表示法：

其中， $\left \| \omega \right \|$ 是向量 $\omega$ ?的模，假如，則，表示在空間中向量的長度。

我們評價分類器的好壞依據是分類間隔的的大小，即分類間隔W越大，我們認為這個超平面的分類效果越好。而追求分類間隔W的最大化也就是尋找 d的最大化。?

? ?

2.3 約束條件

對于SVM的線性可分的二分類問題，我們希望：

1）超平面夠將所有的樣本點都正確分類。
2）超平面的位置應該是在間隔區域的中軸線上。
3）對于一個給定的超平面，我們能找到對應的支持向量，來計算距離d。?

對于上述的三個約束條件，我們假設在平面空間中有紅藍兩種點，對其分別標記為：

紅色為正樣本，標記為+1；
藍色為負樣本，標記為-1。

對每個樣本點? $x_i$ 加上類別標簽 $y_i$ ，則有

如果我們的超平面能夠完全將紅藍兩種樣本點分離開（對應第一個約束條件），那么則有

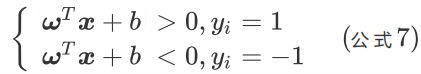
如果要求在再高一點，假設超平面正好處于間隔區域的中軸線上（對應第二個約束條件），并且相應支持向量到超平面的距離為d（對應第三個約束條件），則公式可進一步寫為：

對公式兩邊同時除以d，可得：

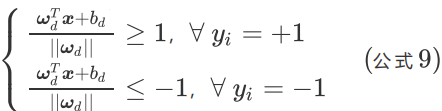
其中，。

簡化方程，使用? $\omega$ 和? $d$ 代替? $\frac{\omega^T _d}{\left \| \omega _d \right \|}$ ， $\frac{b_d}{\left \| \omega _d \right \|}$ ，可得：

當等于 1或 -1時，對應的? $x_i$ 坐標就是支持向量的坐標。

以將上述方程糅合成一個約束方程：

這個方程就是SVM最優化問題的約束條件。

2.4 線性SVM最優化問題

當等于 1或 -1時，對應的? $x_i$ 坐標就是支持向量的坐標，相應的根據約束條件，我們可以知道只有超平面最大化時，?才會等于 1或 -1。無論是等于1還是-1，即? $x_i$ ?為支持向量坐標時，對于公式10來說，都有。

所以對于支持向量來說：

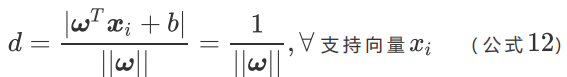
我們原來的任務是找到一組參數 $\omega,b$ 使得分類間隔? $W=2d$ 最大化，根據公式12 就可以轉變為 $\left \| \omega \right \|$ 的最小化問題，也等效于 $\frac{1}{2}\left \| \omega \right \|^2$ 的最小化問題。我們之所以要在 $\left \| \omega \right \|$ 上加上平方和1/2的系數，是為了以后進行最優化的過程中對目標函數求導時比較方便，但這絕不影響最優化問題最后的解。?

所以，線性SVM最優化問題的數學描述就是：

公式13，描述的是一個典型的不等式約束條件下的二次型函數優化問題，同時也是支持向量機的基本數學模型。

? ??

2.5?求解線性SVM最優化問題

有不等式約束條件的原始目標函數求解十分困難，我們需要先轉化沒有約束條件的新目標函數，再進行求導優化，簡單來講過程就是：構造拉格朗日函數?+?求解拉格朗日對偶函數。?

最終得到新的目標函數和約束條件，方便使用高效優化算法SMO算法：

? ?

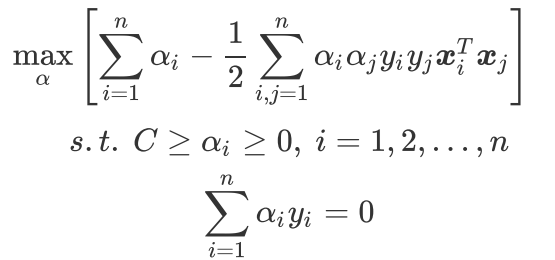
三、SMO算法?

SMO算法就是序列最小優化（Sequential Minimal Optimization），它是由 John Platt 于1996年發布的專門用于訓練SVM的一個強大算法（如同，梯度下降算法專門用于訓練深度學習模型一般）。

簡化版SMO算法，如下：

def smoSimple(dataMatIn, classLabels, C, toler, maxIter):"""smoSimpleArgs:dataMatIn    數據集classLabels  類別標簽C   松弛變量(常量值)，允許有些數據點可以處于分隔面的錯誤一側。控制最大化間隔和保證大部分的函數間隔小于1.0這兩個目標的權重。可以通過調節該參數達到不同的結果。toler   容錯率（是指在某個體系中能減小一些因素或選擇對某個系統產生不穩定的概率。）maxIter 退出前最大的循環次數Returns:b       模型的常量值alphas  拉格朗日乘子"""dataMatrix = mat(dataMatIn)# 矩陣轉置 和 .T 一樣的功能labelMat = mat(classLabels).transpose()m, n = shape(dataMatrix)# 初始化 b和alphas(alpha有點類似權重值。)b = 0alphas = mat(zeros((m, 1)))# 沒有任何alpha改變的情況下遍歷數據的次數iter = 0while (iter < maxIter):# w = calcWs(alphas, dataMatIn, classLabels)# print("w:", w)# 記錄alpha是否已經進行優化，每次循環時設為0，然后再對整個集合順序遍歷alphaPairsChanged = 0for i in range(m):# print 'alphas=', alphas# print 'labelMat=', labelMat# print 'multiply(alphas, labelMat)=', multiply(alphas, labelMat)# 我們預測的類別 y = w^Tx[i]+b; 其中因為 w = Σ(1~n) a[n]*lable[n]*x[n]fXi = float(multiply(alphas, labelMat).T*(dataMatrix*dataMatrix[i, :].T)) + b# 預測結果與真實結果比對，計算誤差EiEi = fXi - float(labelMat[i])# 約束條件 (KKT條件是解決最優化問題的時用到的一種方法。我們這里提到的最優化問題通常是指對于給定的某一函數，求其在指定作用域上的全局最小值)# 0<=alphas[i]<=C，但由于0和C是邊界值，我們無法進行優化，因為需要增加一個alphas和降低一個alphas。# 表示發生錯誤的概率：labelMat[i]*Ei 如果超出了 toler， 才需要優化。至于正負號，我們考慮絕對值就對了。'''# 檢驗訓練樣本(xi, yi)是否滿足KKT條件yi*f(i) >= 1 and alpha = 0 (outside the boundary)yi*f(i) == 1 and 0<alpha< C (on the boundary)yi*f(i) <= 1 and alpha = C (between the boundary)'''if ((labelMat[i]*Ei < -toler) and (alphas[i] < C)) or ((labelMat[i]*Ei > toler) and (alphas[i] > 0)):# 如果滿足優化的條件，我們就隨機選取非i的一個點，進行優化比較j = selectJrand(i, m)# 預測j的結果fXj = float(multiply(alphas, labelMat).T*(dataMatrix*dataMatrix[j, :].T)) + bEj = fXj - float(labelMat[j])alphaIold = alphas[i].copy()alphaJold = alphas[j].copy()# L和H用于將alphas[j]調整到0-C之間。如果L==H，就不做任何改變，直接執行continue語句# labelMat[i] != labelMat[j] 表示異側，就相減，否則是同側，就相加。if (labelMat[i] != labelMat[j]):L = max(0, alphas[j] - alphas[i])H = min(C, C + alphas[j] - alphas[i])else:L = max(0, alphas[j] + alphas[i] - C)H = min(C, alphas[j] + alphas[i])# 如果相同，就沒發優化了if L == H:print("L==H")continue# eta是alphas[j]的最優修改量，如果eta==0，需要退出for循環的當前迭代過程# 參考《統計學習方法》李航-P125~P128<序列最小最優化算法>eta = 2.0 * dataMatrix[i, :]*dataMatrix[j, :].T - dataMatrix[i, :]*dataMatrix[i, :].T - dataMatrix[j, :]*dataMatrix[j, :].Tif eta >= 0:print("eta>=0")continue# 計算出一個新的alphas[j]值alphas[j] -= labelMat[j]*(Ei - Ej)/eta# 并使用輔助函數，以及L和H對其進行調整alphas[j] = clipAlpha(alphas[j], H, L)# 檢查alpha[j]是否只是輕微的改變，如果是的話，就退出for循環。if (abs(alphas[j] - alphaJold) < 0.00001):print("j not moving enough")continue# 然后alphas[i]和alphas[j]同樣進行改變，雖然改變的大小一樣，但是改變的方向正好相反alphas[i] += labelMat[j]*labelMat[i]*(alphaJold - alphas[j])# 在對alpha[i], alpha[j] 進行優化之后，給這兩個alpha值設置一個常數b。# w= Σ[1~n] ai*yi*xi => b = yj- Σ[1~n] ai*yi(xi*xj)# 所以：  b1 - b = (y1-y) - Σ[1~n] yi*(a1-a)*(xi*x1)# 為什么減2遍？ 因為是 減去Σ[1~n]，正好2個變量i和j，所以減2遍b1 = b - Ei- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i, :]*dataMatrix[i, :].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[i, :]*dataMatrix[j, :].Tb2 = b - Ej- labelMat[i]*(alphas[i]-alphaIold)*dataMatrix[i, :]*dataMatrix[j, :].T - labelMat[j]*(alphas[j]-alphaJold)*dataMatrix[j, :]*dataMatrix[j, :].Tif (0 < alphas[i]) and (C > alphas[i]):b = b1elif (0 < alphas[j]) and (C > alphas[j]):b = b2else:b = (b1 + b2)/2.0alphaPairsChanged += 1print("iter: %d i:%d, pairs changed %d" % (iter, i, alphaPairsChanged))# 在for循環外，檢查alpha值是否做了更新，如果在更新則將iter設為0后繼續運行程序# 知道更新完畢后，iter次循環無變化，才推出循環。if (alphaPairsChanged == 0):iter += 1else:iter = 0print("iteration number: %d" % iter)return b, alphas

查看代碼運行時間及結果：?

# 懲罰因子C = 0.6
# 容錯率toler = 0.001
# 退出前最大循環次數maxIter=40
%time b, alphas = smoSimple(dataArr, labelArr, 0.6, 0.001, 40)