
文章目錄
- 🚀前言
- 🚀異或運算以及與運算
- 🚀加法的實現
- 🚀減法的實現
- 🚀乘法的實現
- 🚀除法的實現
🚀前言
這也是阿輝開的新專欄,知識將會很零散不成體系,不過絕對干貨滿滿,今天這一篇利用位運算實現加減乘除費了阿輝九牛二虎之力,干的很自備飲水😆不多bb,進入今天的學習吧!!!
以下int均為有符號int,所求的加減乘除也是int類型的整型數
嚴謹 😏
🚀異或運算以及與運算
在寫加減乘除之前,先給鐵子們介紹一下異或運算以及與運算的其他理解
異或運算:也叫無進位相加
這怎么理解呢?
鐵子們都知道,異或運算,是二進制位相異為1,相同為0
其實異或運算也可以解釋為無進位相加。這是什么意思呢?就是對應的二進制位相加,如果產生進位就將進位舍去。什么是進位呢?對應的二進制位相加為2時就向前進一位,就像我們小時候學的加法一樣。而二進制進位后,本位就剩下一個0。而在異或運算中,進位被舍去,所以當兩個位都為1時,異或的結果為0;當兩個位都為0時,異或的結果也為0;只有一個位為1,另一個位為0時,異或的結果才為1
給鐵子們上圖解釋:
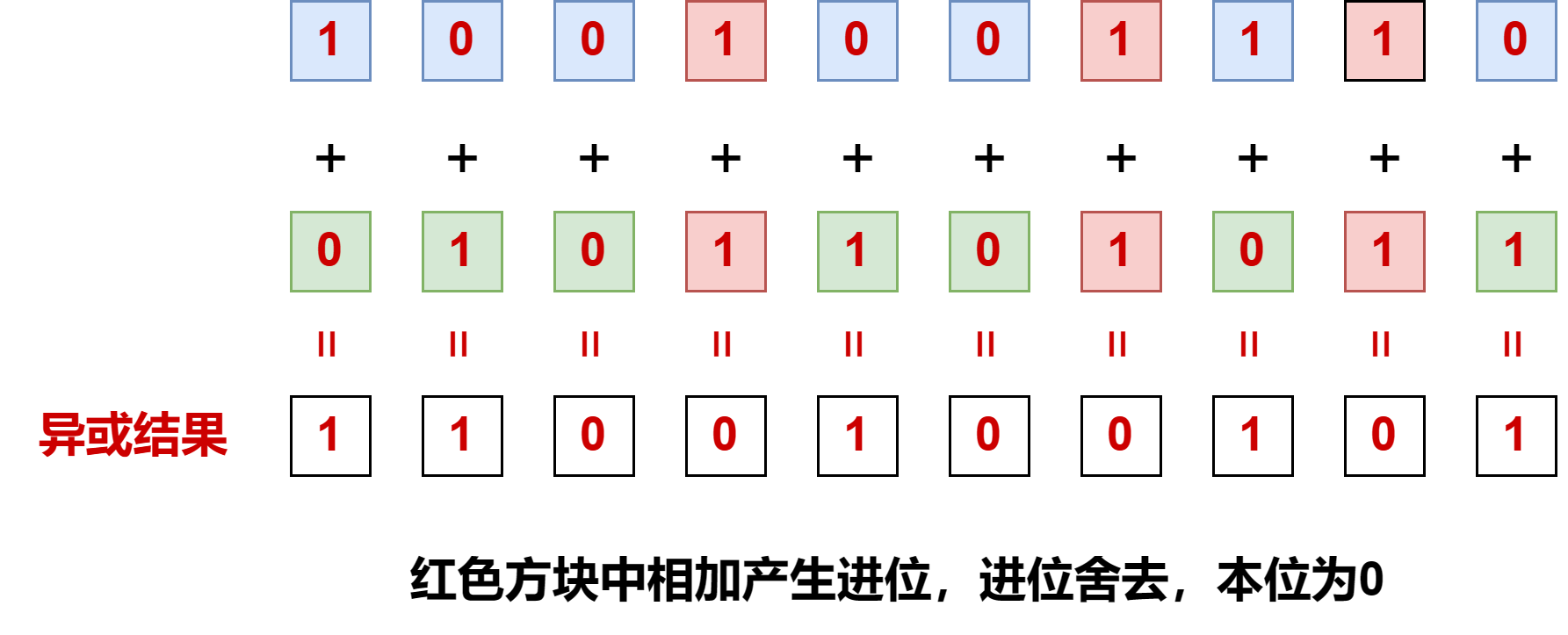
與運算:得到對應二進制位相加的進位信息右移一位后的結果
怎么理解呢?
鐵子們都知道,與運算,是兩二進制位都為1為1,一個為0就為0
實際上,與運算是得到對應二進制位相加的進位信息右移一位后的結果,怎么理解呢?二進制位相加時產生的進位保留,沒有進位舍去直接置0,然后將得到的結果右移一位。
給鐵子們上圖解釋:
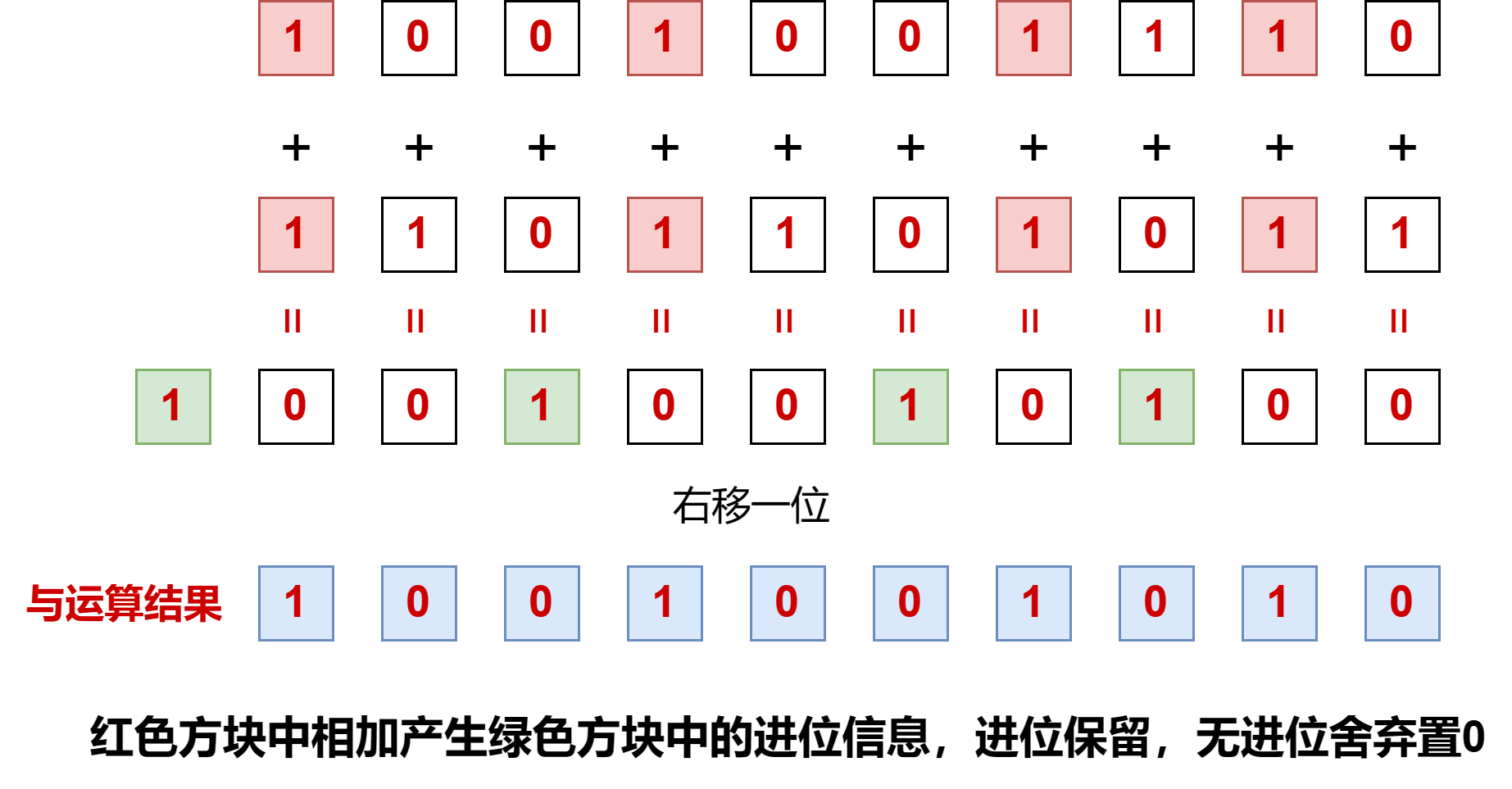
🚀加法的實現
有了上述關于異或運算和與運算的新的理解,基于此,我們可以用他們拼湊出加法,怎么拼呢?鐵子們接著看👇
根據前面的講解我們知道,兩個數異或運算得到的是兩個數相加去掉進位信息后的結果,而兩個數與運算得到的是兩個數相加保留進位信息右移一位后的結果,鐵子們,睜大眼騷操作來了😏,異或運算是去掉進位信息的結果,與運算結果再左移一位(進位信息右移了嘛,再左移回去)是保留進位信息的結果,那兩個數異或運算的結果加上兩個數與運算再左移一位的結果不就是兩個數相加的結果嘛;
鐵子們一定會說這不還得在加一遍,有毛用,別急還有更騷的😏😏,兩個數的異或運算的結果和與運算左移一位的結果,只要與運算左移一位的結果不為0也就是進位信息不為0,得到的倆個數重復上述操作,直到進位信息為0,異或運算的結果不就是兩數相加的結果嘛。鐵子們,騷不騷?覺得騷的,記得在評論區給阿輝扣個666 😘
肯定有老鐵會說難道進位信息一定會計算到0嗎?好問題哈哈哈哈 😜,一定會計算到0,為什么呢?阿輝用圖說明,鼠標寫的鐵子們湊合看一下🙏

異或運算就是把二進制數相加得到如上述不加上藍色進位信息的結果,然后和進位信息繼續異或,直到不在產生進位信息得到相加的結果
如果還有鐵子不懂,可以私聊阿輝加個微信,阿輝必給你搞明白,上面進位信息為啥一定會算到0是阿輝自己想的,自認還有點騷,哈哈哈 😁!
下面就是代碼實現了,別看講了這一堆,其實代碼很好寫
int Add(int x, int y)//傳入需要需要相加的數
{while (y)//y就是進位信息,為0時跳出循環{int a = x ^ y;//利用臨時變量保證下一步計算進位信息x不變y = (x & y) << 1;//進位信息x = a;//把去掉進位信息的結果賦給a,重復上述操作}return x;
}
代碼就這么短,騷不騷?哈哈哈,這篇博客寫的爽,鐵子們后面的內容更騷,嘿嘿嘿!!!
🚀減法的實現
減法就沒什么技術含量了,因為比如5-4還可以寫成5+(-4),套上前面寫的加法然后,給減數改成相反數即可
相反數怎么整?讓阿輝裝一手,嘿嘿
原反補碼,阿輝就不講了,默認大家都會
按位取反操作符~,一個數取反后,符號位會改變,這么一整,該數的正負相反了,符號位以外的數也取反了,如果再加個1,大家不看符號位這不就是負數原碼得到補碼的過程,喲,這不拿捏了-a = ~a + 1
代碼不就好寫了:
int Sub(int x, int y)//傳入被減數與減數
{return Add(x, ~y + 1);//減數取相反數后與被減數相加
}
🚀乘法的實現
乘法也是稀松平常,沒什么難理解的地方,怎么實現呢?鐵子們別急,阿輝整個例子你們就懂了👊
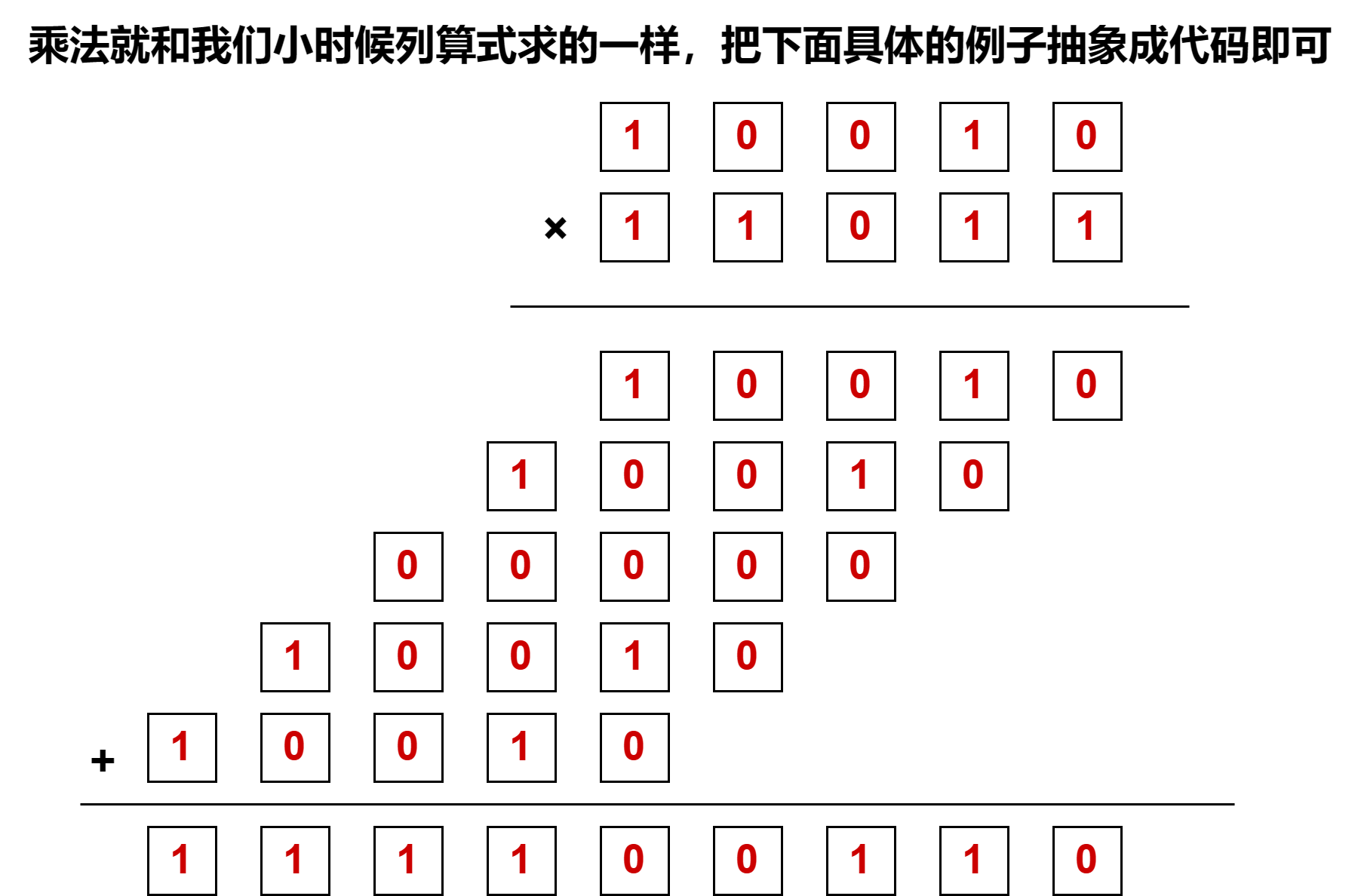
鐵子們這里阿輝,先給出代碼再解釋:
int Mul(int x, int y)//傳進來兩數
{int ret = 0;//作返回值for (int i = 0; i <= 30; i = Add(i, 1))//符號位不算,固定循環31次{//遍歷y的除符號位的31位,判斷是否為1if (y >> i & 1 == 1)//對應二進制位為1,進入if{//因為二進制位只有0和1,0乘任何數還是0,所以不用管//當為1時,1乘任何數還是它本身,所以加上xret = Add(ret, x);}//遍歷一次x左移一位,因為再循環,y向后一位找1//這個1代表2的i次方,相當于把這個2的i次方乘在了x上//左移一位相當于乘2,右移一位相當于除2x <<= 1;}return ret;
}
鐵子們注意,上述實現的乘法可以計算負數,為什么呢?這與原反補碼有關,阿輝水平有限解釋不出來,鐵子們感興趣可以研究一下,找到記得和阿輝分享一波,嘿嘿
鐵子們,沒懂的話可以自己想想試試,如果實在不懂可以私信我好吧,下面的除法才是重頭戲特別麻煩 💀
🚀除法的實現
除法比較麻煩,這里阿輝實現的除法是整數除法,上圖給大家引導:
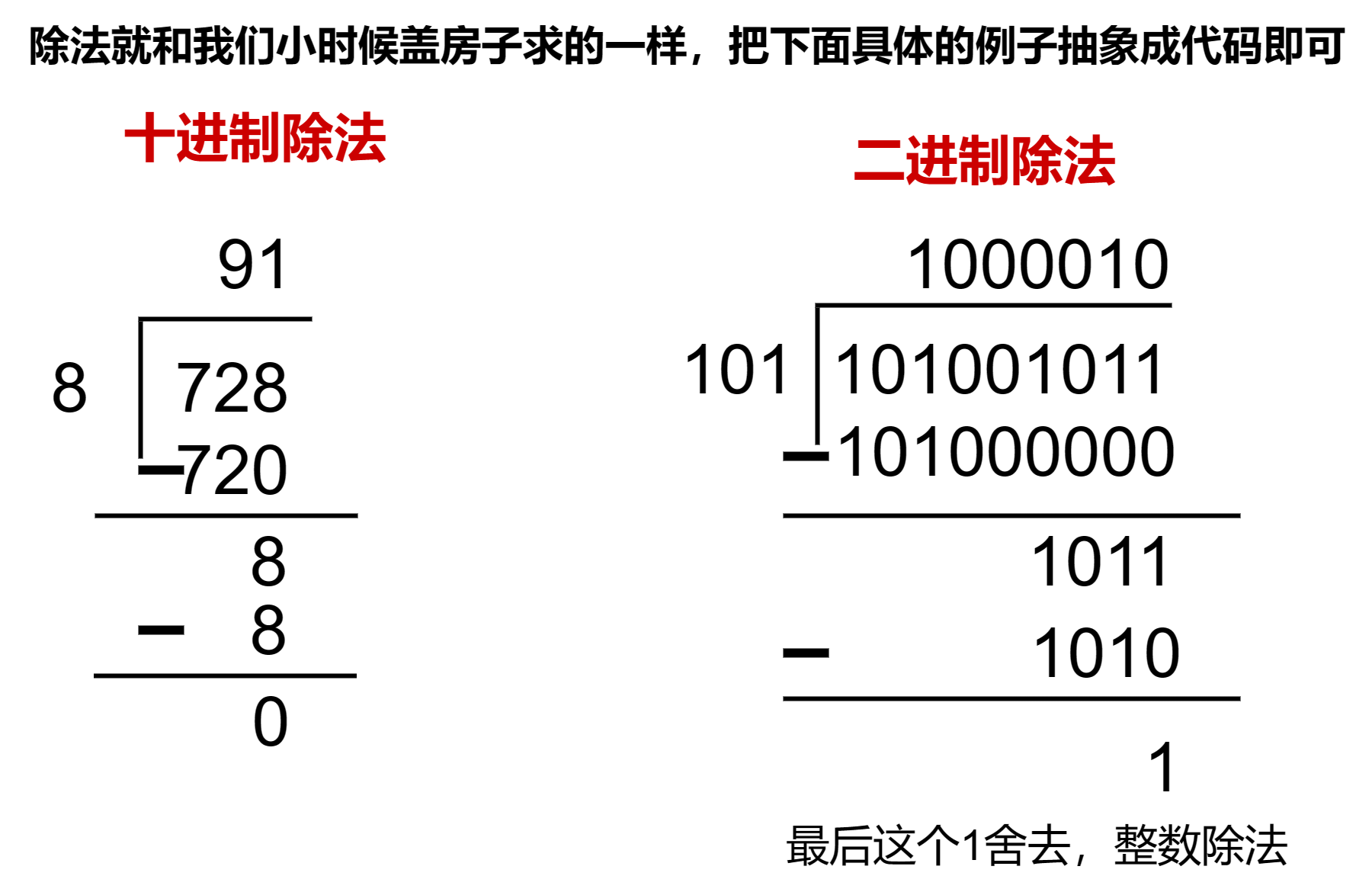
關于將除法抽象成代碼,這是一個相當復雜的過程。首先,讓我們回顧一下如何進行除法運算。在我們最常見的十進制系統中,以被除數728÷8為例,我們是如何得出十位上的9的呢?除法運算實際上是在找到一個最大的數,使得將除數8乘以這個數接近被除數728,然后再用728減去這個數720(8×90),然后繼續這個過程,要么除盡要么除不盡。不過在整數除法中,如果除不盡就舍去余數。實際上,二進制數的除法運算也是類似的過程。與十進制不同的是,二進制位只有1,因此只需要將除數101后面加上0來逼近被除數101001011(在二進制中,將除數101左移一位就相當于除數后面加上一個0),然后用101001011減去101×1000000(101左移6位),然后重復這個操作直到除盡
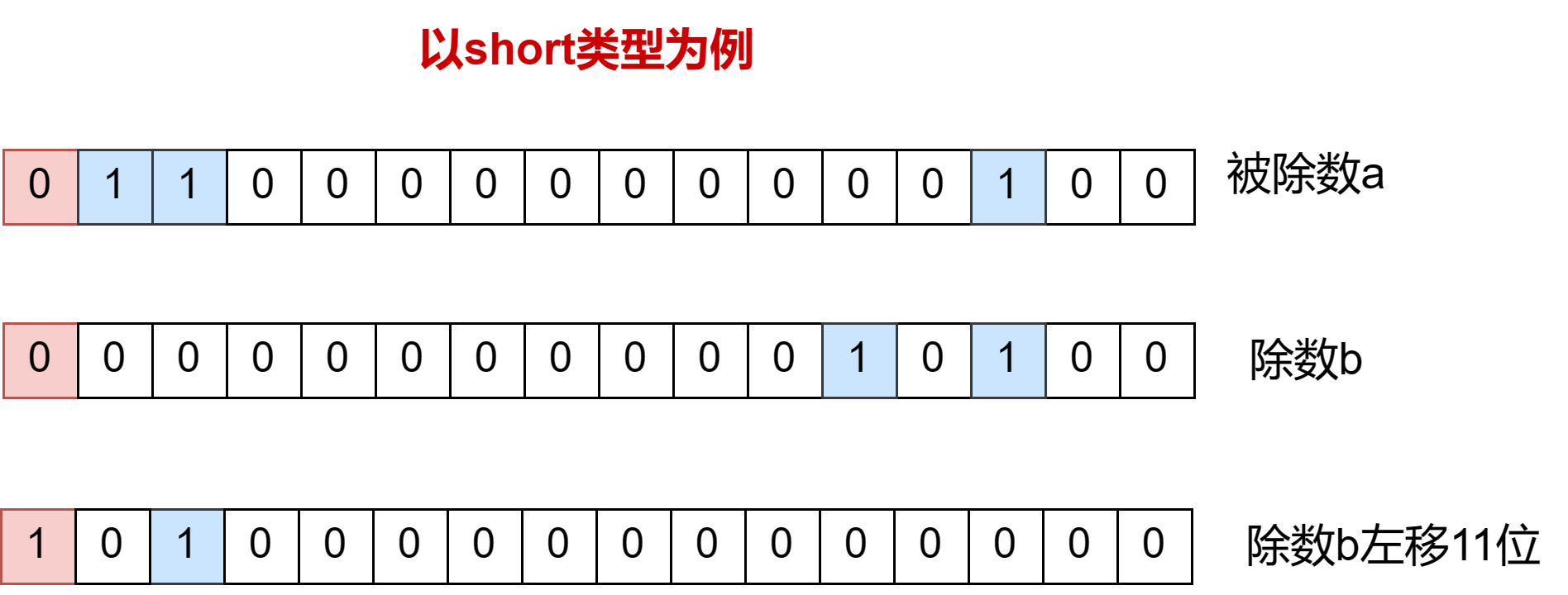
但是我們在寫代碼時不能通過除數左移去逼近,因為這樣會有風險
紅色方塊的位置代表符號位。我們給除數b左移,左移一位比a小,繼續左移直到比a大才知道上一次左移逼近被除數a。但是對于我們給的這個例子b怎么左移也不可能比a大,因為當b右移11位時,符號位變成1了,b直接變成負數了。
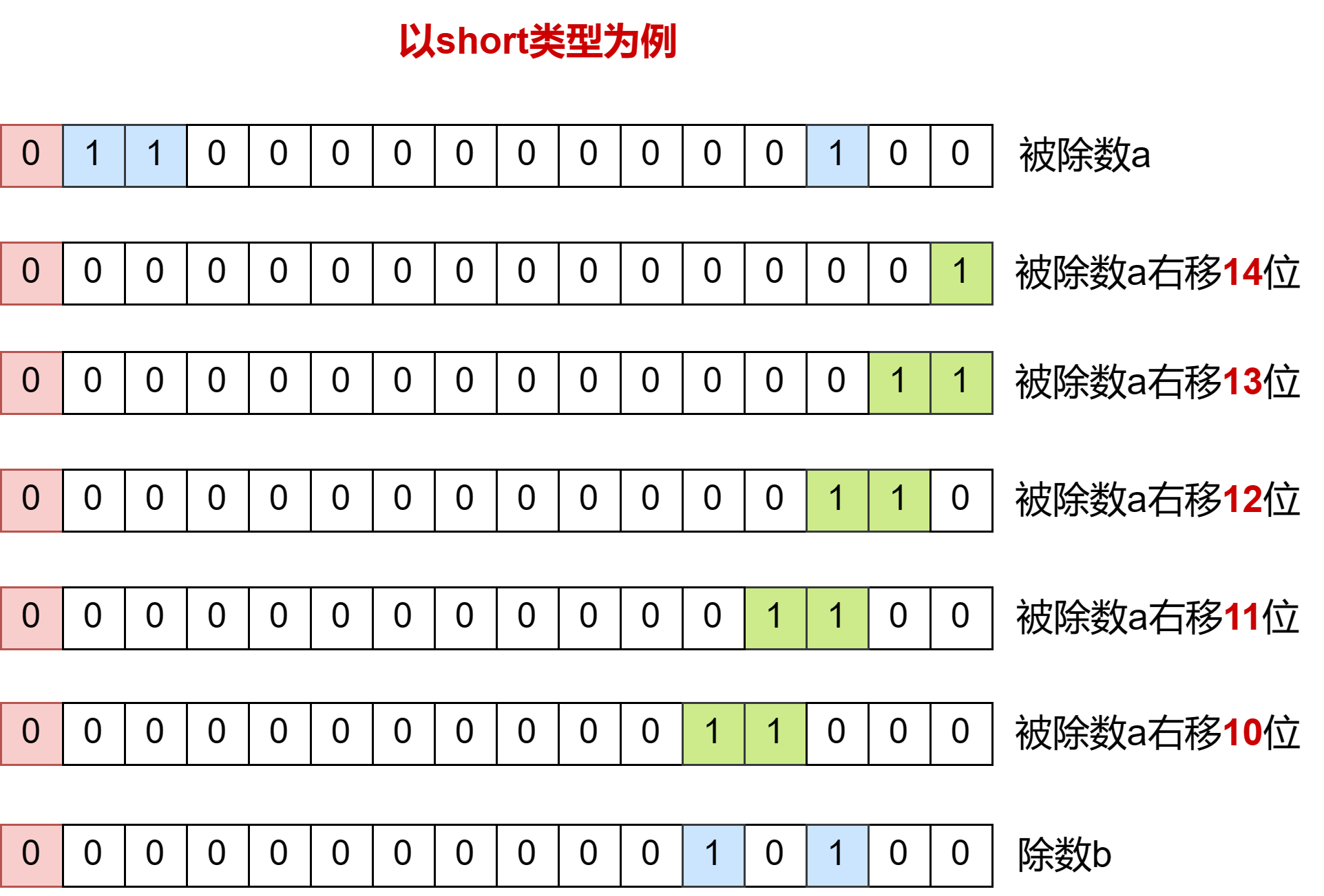
這里我們通過被除數右移代替除數左移來逼近除數達到一樣的效果,因為被除數右移多少位逼近除數也就是除數左移多少位逼近被除數,這樣就不會有改變符號位的風險
我們讓除數a從右移14位開始,然后右移位數依次遞減,當a右移10位時第一次大于b也就是b左移10位逼近a,然后a減去b左移10位后的數得到的結果重復上述操作第一次找到的就是最高位的1就像我們算十進制除法一樣,我們首先找到千位隨后就是百位、十位只不過二進制只有0和1很多位都是0
鐵子們,下面我會根據代碼講,盡我所能講明白好吧!
首先,我們實現的除法并不能處理負數,要先把負數處理成正數
這里我們實現一個函數oppo()求相反數
int oppo(int x)//相反數
{return Add(~x, 1);//上面減法的時候解釋過了
}
下面是關于除法的具體實現(不包括系統最小值)
int dived(int x, int y)//不含系統最小數的除法
{//負數改正數,正數則不變int a = x < 0 ? oppo(x) : x;//小于0就取相反數int b = y < 0 ? oppo(y) : y;int ret = 0;//作返回值//除了符號位,遍歷31次for (int i = 30; i >= 0; i = Sub(i, 1)){//i從30開始依次遞減//當a第一次右移i位大于b時,說明最高位的數字找到了//進入if把值加到返回值ret上if (a >> i >= b){ret |= 1 << i;//ret初始值時0,把1或上去a = Sub(a, Mul(b,ret));//同時更新a的值,a=a-b×ret}}//只有x和y不同時為負數或正數時要取相反數//x,y同時大于或小于0,相除就是正數嘛//異或值相等為0嘛就是假//這個異或騷不騷,代替了下面這么挫的代碼//if((x > 0 && y < 0) || (x < 0 && y > 0))if (x > 0 ^ y > 0)return oppo(ret);//取相反數return ret;
}
包含系統最小值,int類型的取值為-2^30^ ~ 0 ~ 2^30^-1,因為0是包含在正數里的,所以系統最小值的絕對值大于系統最大值,所以我們面臨一個問題,系統最小值沒有它的相反數,所以求系統最小值我們要單獨拎出來求
五種情況(x是被除數,y是除數):
- x,y都是系統最小,直接返回
1 - y是系統最小,x不是,直接返回
0(整數除法) - x是系統最小,y是-1,那結果就是系統最小的絕對值,值域沒這個數,直接返回-1
- x,y都不是系統最小,咱們上面實現的那個代碼就是
- x是系統最小,y不是,這個情況就是我們下面要解決的
x是系統最小,y不是,這里我們無法給它取相反數,我們給x拆成兩部分,
a=(x+1)得到的就不是系統最小了,用b = (a÷y),可以用我們上面的dived()這個函數來求,然后在用c = x - (b × y),接著a = c ÷ y,最后a+b就是x÷y的結果
就是上面這張圖這個原理,沒啥難的,不一定要加1,2、3、4……都可以
INT_MIN被宏定義成int類型的最小值,使用需要引<limits.h>頭文件
int Div(int x, int y)
{if (x == INT_MIN && y == INT_MIN)return 1;else if (x == INT_MIN && y == -1)return -1;else if (y == INT_MIN)return 0;//這就是上面解釋的代碼else if (x == INT_MIN){int a = Add(x, 1);int b = dived(a, y);a = dived(Sub(x, Mul(b, y)), y);return Add(a, b);}elsereturn dived(x,y);//不含系統最小值的除法
}
coding有三點要注意:
- 負數要先轉化成正數
- 被除數左移會有風險
- 系統最小無法取相反數
加減乘除的完整代碼,他們并不是孤立的,互相調用
#include<stdio.h>
#include<limits.h>
int Add(int x, int y)
{while (y){int a = x ^ y;y = (x & y) << 1;x = a;}return x;
}int Sub(int x, int y)
{return Add(x, Add(~y, 1));
}
int Mul(int x, int y)
{int ret = 0;for (int i = 0; i <= 30; i = Add(i, 1)){if (y >> i & 1 == 1){ret = Add(ret, x);}x <<= 1;}return ret;
}int oppo(int x)
{return Add(~x, 1);
}int dived(int x, int y)
{int a = x < 0 ? oppo(x) : x;int b = y < 0 ? oppo(y) : y;int ret = 0;for (int i = 30; i >= 0; i = Sub(i, 1)){if (a >> i >= b){ret |= 1 << i;a = Sub(a, Mul(b,ret));}}if (x > 0 ^ y > 0)return oppo(ret);return ret;
}int Div(int x, int y)
{if (x == INT_MIN && y == INT_MIN)return 1;else if (x == INT_MIN && y == -1)return -1;else if (y == INT_MIN)return 0;else if (x == INT_MIN){int a = Add(x, 1);int b = dived(a, y);a = dived(Sub(x, Mul(b, y)), y);if (x > 0 ^ y > 0)return oppo(Add(a, b));return Add(a, b);}elsereturn dived(x,y);
}
好的,到這里阿輝就講完了,說實話不容易,著力于構思怎么把鐵子們講懂,應該沒有比我更細節的了,寫完這篇滿滿成就感,鐵子們覺得講得不錯的話給阿輝評論區扣個666,哈哈哈!!!!

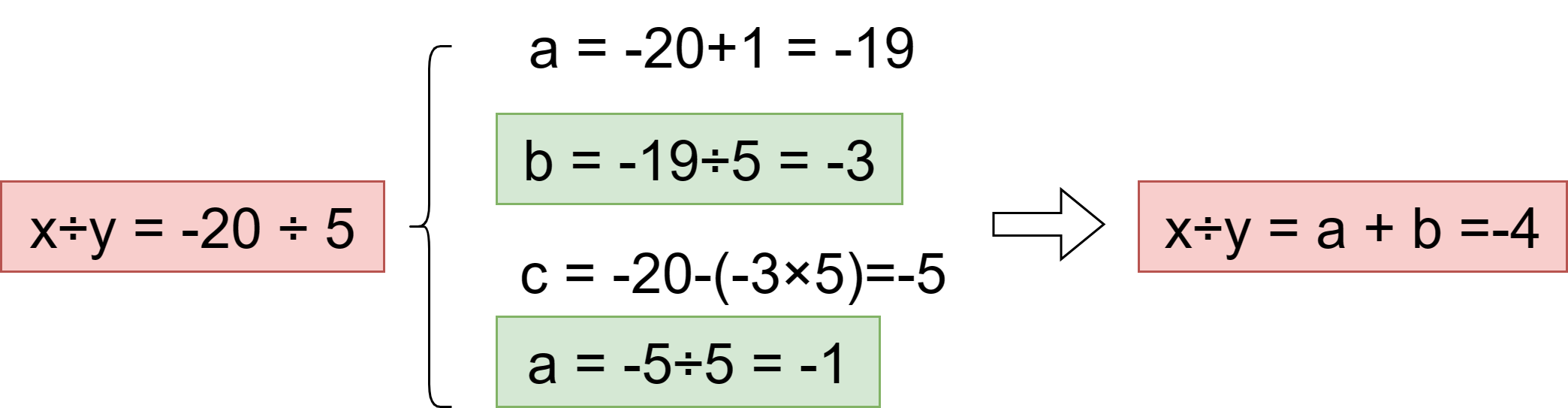



:RK3568底板電路mipi攝像頭接口原理圖分析、mipi攝像頭詳解)









)


)
)
)
![力扣每日一題day34[110. 平衡二叉樹]](http://pic.xiahunao.cn/力扣每日一題day34[110. 平衡二叉樹])