給定一個二叉樹，判斷它是否是高度平衡的二叉樹。

本題中，一棵高度平衡二叉樹定義為：

一個二叉樹每個節點?的左右兩個子樹的高度差的絕對值不超過 1 。

示例 1：

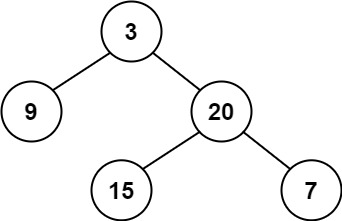
輸入：root = [3,9,20,null,null,15,7]
輸出：true

示例 2：

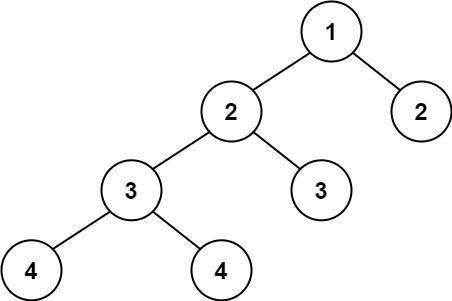
輸入：root = [1,2,2,3,3,null,null,4,4]
輸出：false

示例 3：

輸入：root = []
輸出：true

• 二叉樹節點的深度：指從根節點到該節點的最長簡單路徑邊的條數。

• 二叉樹節點的高度：指從該節點到葉子節點的最長簡單路徑邊的條數。

但leetcode中強調的深度和高度很明顯是按照節點來計算的

關于根節點的深度究竟是1 還是 0，不同的地方有不一樣的標準，leetcode的題目中都是以節點為一度，即根節點深度是1。

遞歸三步曲分析：

明確遞歸函數的參數和返回值

參數：當前傳入節點。 返回值：以當前傳入節點為根節點的樹的高度。

那么如何標記左右子樹是否差值大于1呢？

如果當前傳入節點為根節點的二叉樹已經不是二叉平衡樹了，還返回高度的話就沒有意義了。

所以如果已經不是二叉平衡樹了，可以返回-1 來標記已經不符合平衡樹的規則了。

代碼如下：

// -1 表示已經不是平衡二叉樹了，否則返回值是以該節點為根節點樹的高度
int getHeight(TreeNode root)

明確終止條件

遞歸的過程中依然是遇到空節點了為終止，返回0，表示當前節點為根節點的樹高度為0

代碼如下：

if (root == null) {return 0;
}

明確單層遞歸的邏輯

如何判斷以當前傳入節點為根節點的二叉樹是否是平衡二叉樹呢？當然是其左子樹高度和其右子樹高度的差值。

分別求出其左右子樹的高度，然后如果差值小于等于1，則返回當前二叉樹的高度，否則返回-1，表示已經不是二叉平衡樹了。

class Solution {public boolean isBalanced(TreeNode root) {return getHeight(root) != -1;}
?private int getHeight(TreeNode root) {if (root == null) {return 0;}int leftHeight = getHeight(root.left);if (leftHeight == -1) {return -1;}int rightHeight = getHeight(root.right);if (rightHeight == -1) {return -1;}// 左右子樹高度差大于1，return -1表示已經不是平衡樹了if (Math.abs(leftHeight - rightHeight) > 1) {return -1;}return Math.max(leftHeight, rightHeight) + 1;}
}