【三維重建】對極幾何

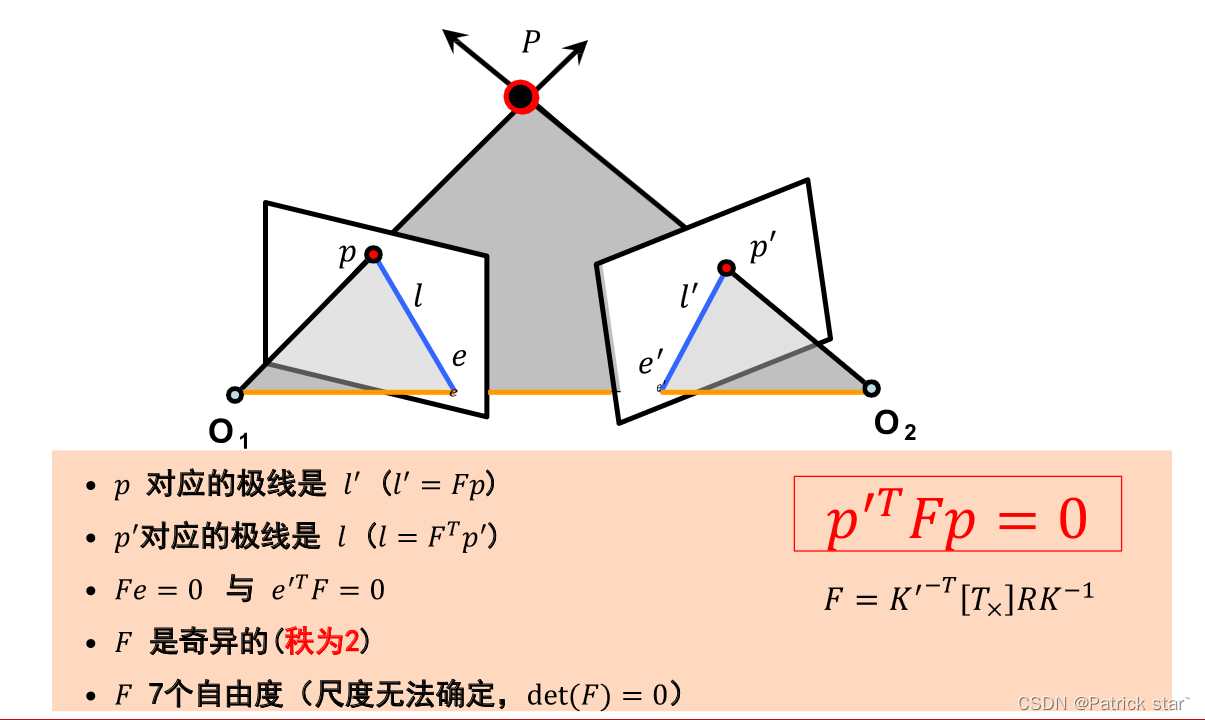
極幾何描述了同一場景或者物體的兩個視點圖像間的幾何關系

可以發現Ｐ在左右相機的投影點一定在各自的極線上，如果求出極線就能縮小求解對應點的范圍。

本質矩陣對規范化攝像機拍攝的兩個視點圖像間的極幾何關系進行代數描述

規范化相機指的是相機的內參矩陣為一個單位矩陣

$P'=\begin{bmatrix} x\\y \\ z \end{bmatrix}=\begin{bmatrix} 1 &0 & 0 & 0\\ 0&1 &0 &0 \\ 0& 0 & 1 & 0 \end{bmatrix} \begin{bmatrix} x\\y \\ z \\ 1 \end{bmatrix} \ \ P'=MP$ ?????

設 $p'^*$ 是 $p'$ 在 $O_1$ 坐標系下的坐標，則：

$p'=Rp'^*+T \rightarrow p'^*=R^Tp'-R^TT(R^{-1} = R^T)$

因此， $p'$ 在 $O_1$ 坐標系下的坐標為　 $R^Tp'-R^TT$

同理： $O_2$ 在 $O_1$ 坐標系下的坐標為　 $-R^TT$

得到兩個向量　 $O_1p' \ , O_1O_2$

$O_1p' \times O_1O_2 = R^TT \times (R^Tp'-R^TT)=R^TT \times R^Tp'$ （垂直于極平面）

$[R^TT \times R^Tp']^T \cdot p = 0$

$a \times b$ 可以寫成一個矩陣乘積的形式，比如：

$a = (x_1,y_1,z_1),b=(x_2,y_2,z_2)$

$a \times b = (y_1z_2-z_1y_2,z_1x_2-x_1z_2,x_1y_2-y_1x_2)\\ = \begin{bmatrix} 0& -z_1 &y_1 \\ z_1&0 &-x_1 \\ -y_1&x_1 &0 \end{bmatrix}\begin{bmatrix} x_2\\y_2 \\ z_2 \end{bmatrix}$

因此，

$[R^TT \times R^Tp']^T \cdot p = [T \times p']^TRp=[T_xp']^TRp \\ \\ =p'^TT_x^TRp=p'^TT_xRp=p'^T[T \times R]p = 0$

（　 $T_x$ 　是一個秩為２的對稱矩陣）

$E = T \times R = T_{\times}R$

E就是本質矩陣，描述了規范化攝像機下兩個視點的關系。

$p^T \cdot l = 0 ,\ p'^TEp =0\rightarrow l =E^Tp' \\ p'^T \cdot l' = 0 ,\ p'^TEp =0\rightarrow l' =Ep$

e也是極線ｌ上的點，所以

$l^Te = p'^TEe=0\rightarrow Ee =0$

基礎矩陣對一般的透視攝像機的兩個視點的圖像間的極幾何關系進行代數描述

核心思想是將一般相機下的 $p,p'$ ，變成規范化相機下的 $p,p'$

$p=K[I\ O]P\rightarrow K^{-1}p=K^{-1}K[I \ O]P\rightarrow \begin{bmatrix} 1 &0 &0 &0 \\ 0& 1& 0&0 \\ 0 & 0&1 & 0 \end{bmatrix}P$

$let \ \begin{bmatrix} 1 &0 &0 &0 \\ 0 & 1 & 0 &0 \\ 0 & 0 & 1 & 0 \end{bmatrix}P = p_c\rightarrow p_c = K^{-1}p \ , p_c '= K'^{-1}p'$

$p_c',p_c$ 符合規范換相機要求，因此：

$p_c'Ep_c=p_c'^T[T_{\times}]Rp_c=(K'^{-1}p' )^T [T_{\times}]RK^{-1}p \\ \\ =p'^TK'^{-T}[T_{\times}]RK^{-1}p = 0$

$let F=K'^{-T}[T_{\times}]RK^{-1},\ p'^TFp=0$

F就是基礎矩陣，反映了一般相機下，兩視點間的關系。

求解基礎矩陣

用對應點求解Ｆ

求出的 $\hat{F}$ 往往是滿秩的，而我們所要求的基礎矩陣秩為２

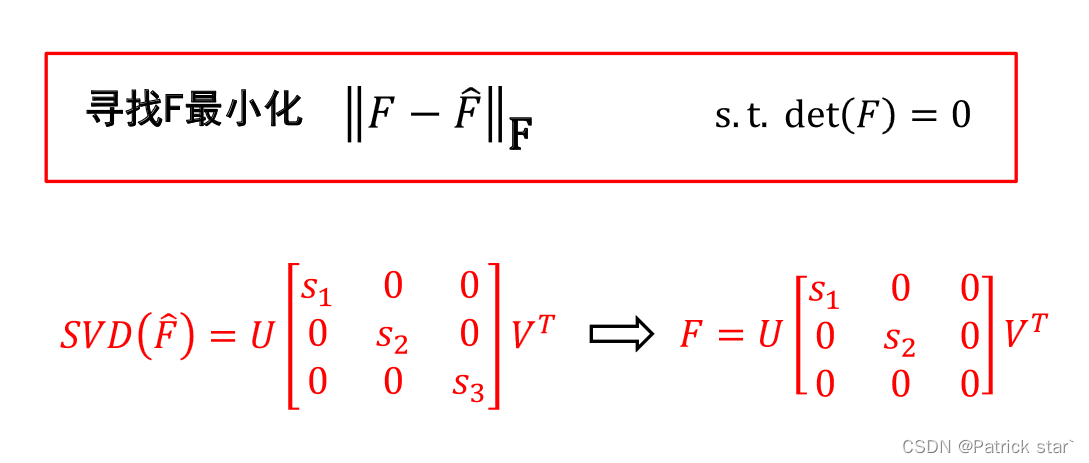
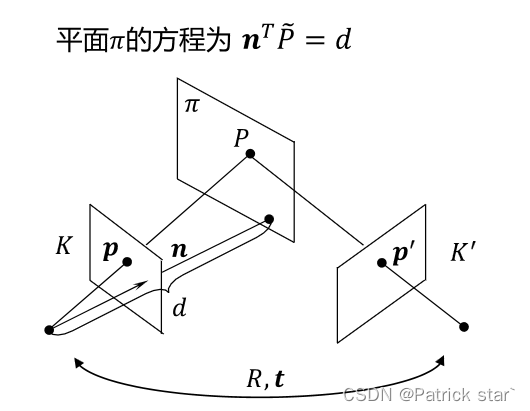
單應性矩陣

如果采集到的對應點在同一平面，兩個視點間的對應關系用單應性矩陣表示

$M = K(I \ O),\ M' = K'(I\ O),\ P= (\tilde{P^T},1)^T \\ \\ p = M\begin{pmatrix} \tilde{P}\\1 \end{pmatrix} =K \tilde{P} \\ \\ p' = M'\begin{pmatrix} \tilde{P}\\1 \end{pmatrix}=K'(R \ t)\begin{pmatrix} \tilde{P} \\1 \end{pmatrix}=K'(R \tilde{P} + t)$

$n^T \tilde{P} = d \rightarrow n^T \tilde{P} / d = 1 \\ \\ let \ n / d = n_d , n_d^T \tilde{P} = 1$

? $p'=K'(R\tilde{P} + t \cdot n_d^T \tilde{P}) = K'(R + t \cdot n_d^T)\tilde{P} =K'(R + t \cdot n_d^T)K^{-1}p$

本質矩陣 $H = K'(R + t \cdot n_d^T)K^{-1}$

參考內容：計算機視覺之三維重建（深入淺出SfM與SLAM核心算法）—— 4. 三維重建基礎與極幾何_嗶哩嗶哩_bilibili

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/215118.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/215118.shtml
英文地址，請注明出處：http://en.pswp.cn/news/215118.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！