一、選擇排序——時間復雜度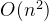

定義：第一趟排序，從整個序列中找到最小的數，把它放到序列的第一個位置上，第二趟排序，再從無序區找到最小的數，把它放到序列的第二個位置上，以此類推。

????????也就是說，首先從序列中找到最小的元素，放到有序區的第一個位置上，然后再從剩下的無序區中，繼續找最小的元素，放到有序區的末尾。

1、容易想到的方法——不推薦

????????新建一個空列表，然后每遍歷一次老列表時候，就把一個最小值，放到新列表里，同時再把這個值從老列表里刪除掉。

但這種方法有兩個缺點：

（1）額外占內存。因為新建了一個空列表 l1，所以就會多占用一個內存空間。

（2）時間復雜度高，排序效率慢。

????????列表的增加和刪除方法，時間復雜度都是O(n)。

????????原因：把最小值加到新列表里，首先要先找到最小值，而找最小值的過程，其實就是把所有值都遍歷一遍，所以，增加的操作，時間復雜度式O(n)。

????????同理，對于刪除操作也一樣，你要刪掉最小值，首先得找到，而找最小值的過程就是要把列表全部遍歷一遍，時間復雜度也是O(n)。

????????所以，法1中，增加和刪除操作，它倆時間復雜度其實也就是O(n)+O(n)，因為他倆是并行運行的，不是嵌套運行，所以結果還是O(n)。外面還有一個for循環，所以法1代碼，復雜度就是。

# 法1
def select_sort_simple(li):  l1 = []for i in range(len(li)):  # 時間復雜度o(n)l1.append(min(li))   li.remove(min(li)) return l1result = select_sort_simple([5, 3, 7, 2, 4])
print(result)# 結果：
[2, 3, 4, 5, 7]

????????或許你會說，把最小值，賦值給一個變量，比如，a=min(li)，然后每次增加刪除這個值，結果還一樣嗎？答案是肯定一樣的，因為，你即使把它賦值給一個變量，但前提，你也得先找到這個最小值，而找最小值的過程就是把列表所有值都遍歷一遍，此時它的復雜度就已經是了，再加上外面的for循環，代碼整體復雜度還是。

# 法2 最小值，賦值給一個變量
def select_sort_simple(li):  l1 = []for i in range(len(li)):  # 時間復雜度 O(n)a=min(li)   # 時間復雜度 O(n)l1.append(a)   li.remove(a)  return l1result = select_sort_simple([5, 3, 7, 2, 4])
print(result)
# 結果同上

2、使用切片的方式控制無序區——推薦

????????使用切片的方式控制無序區，每一趟排序后，都將無序區中的最小值，放到無序區的第一個位置，也就是說，把無序區的最小值跟無序區的第一個元素進行交換，此時，這個最小值也就自然放到了有序區的末尾。

跟上面方法相比，雖然時間復雜度一樣，但是不用新建空列表。

# 推薦！！！
def select_sort(li): for i in range(len(li) - 1):  # 總共要排n-1趟min_val = min(li[i:])  # !!! 每遍歷一次，無序區就會少一個數a = li.index(min_val)  # 找到最小值的下標li[i], li[a] = li[a], li[i]  # 每趟遍歷，就把最小值與這趟對應位置上的數進行交換# 或者說，就是把無序區的最小值與無序區第一個數進行交換return liresult = select_sort([5, 1, 2, 4])
print(result)
# 結果：
[1, 2, 4, 5]

效果圖：?

當然也可以輸出每趟排序的結果，結果跟上圖也是一樣的：

def select_sort(li):for i in range(len(li) - 1):  # 總共要排n-1趟min_val = min(li[i:])  a = li.index(min_val)  # 找到最小值的下標li[i], li[a] = li[a], li[i] print(li)  # ！！每趟排序后的結果return liresult = select_sort([5, 1, 2, 4])
print("最終排序結果", result)# 結果：
[1, 5, 2, 4]
[1, 2, 5, 4]
[1, 2, 4, 5]
最終排序結果 [1, 2, 4, 5]

上面方法中，使用的是切片來控制無序區的大小，（或者叫范圍），然后再從這個范圍里找最小值，這里呢，我們也可以使用?for 循環的形式來控制無序區的范圍。代碼如下：

這個跟上面方法類似，但利用切片方式控制無序區范圍，相比for循環會更加簡潔明了，所以推薦切片的方法。

def select_sort(li):for i in range(len(li) - 1):  # 總共要排n-1趟min_loc = i  # 假設無序區的第一個數是最小數for j in range(i+1, len(li)):  # 遍歷無序區if li[j] < li[min_loc]:  # 如果無序區中，有個數比無序區第一個數小min_loc = j  # 改變最小值的下標li[i], li[min_loc] = li[min_loc], li[i]  # 將無序區第一個數與最小數進行交換print(li)  # 每趟排序后的結果return li# result = select_sort([3, 4, 2, 1, 5, 6, 8, 7, 9])
result = select_sort([5, 1, 2, 4])
print("最終排序結果", result)# 結果：
[1, 5, 2, 4]
[1, 2, 5, 4]
[1, 2, 4, 5]
最終排序結果 [1, 2, 4, 5]