今天和大家來看看漢諾塔問題，這也是一個經典的算法

漢諾塔問題

分治算法經典問題：漢諾塔問題

漢諾塔的傳說

漢諾塔：漢諾塔（又稱河內塔）問題是源于印度一個古老傳說的益智玩具。大梵天創造世界的時候做了三根金剛石柱子，在一根柱子上從下往上按照大小順序摞著 64 片黃金圓盤。大梵天命令婆羅門把圓盤從下面開始按大小順序重新擺放在另一根柱子上。并且規定，在小圓盤上不能放大圓盤，在三根柱子之間一次只能移動一個圓盤。

假如每秒鐘一次，共需多長時間呢？移完這些金片需要 5845.54 億年以上，太陽系的預期壽命據說也就是數百億年。真的過了 5845.54 億年，地球上的一切生命，連同梵塔、廟宇等，都早已經灰飛煙滅。

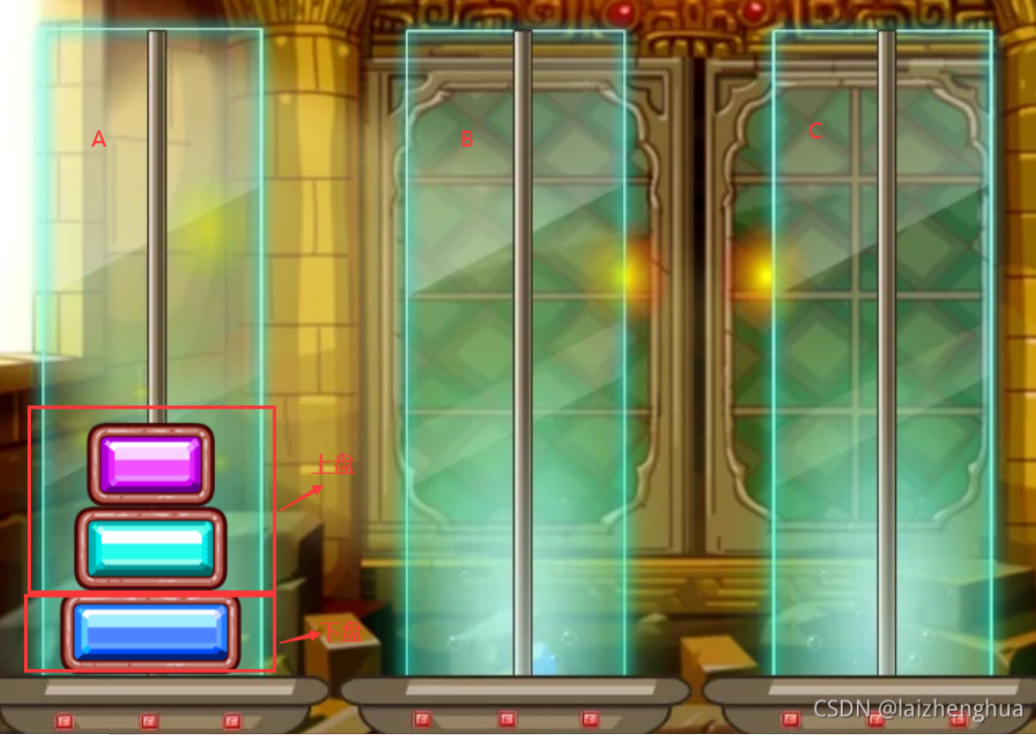
體驗完后，我們來整理下移動盤子的思路（假設有A、B、C柱子）：

1、如果只有一個盤，直接可以A->C

2、如果盤子的數量 n >= 2，我就可以看做是兩個盤子。。

• 最下邊（最大）的盤
• 上面的盤

因此就可以走三部曲

先把最上面的盤A->B
把最下邊的盤A->C
把B塔的所有盤從B->C

代碼示例：

/*** 漢諾塔問題解決* @param discNum 盤子數量* @param a A柱子* @param b B柱子* @param c C柱子*/
public static void towerOfHanoi(int discNum, char a, char b, char c) {// 如果只有一個盤if (discNum == 1) {System.out.println("第1個盤" + a + "->" + c);} else {// 盤的數量 >= 2// 1.上盤A->BtowerOfHanoi(discNum - 1, a, c, b);// 2.下盤A->CSystem.out.println("第" + discNum + "個盤" + a + "->" + c);// 3.把B柱子的所有盤子移至C柱子towerOfHanoi(discNum - 1, b, a, c);}
}