0 前言

🔥 優質競賽項目系列，今天要分享的是

🚩 卷積神經網絡手寫字符識別 - 深度學習

該項目較為新穎，適合作為競賽課題方向，學長非常推薦！

🥇學長這里給一個題目綜合評分(每項滿分5分)

• 難度系數：3分
• 工作量：3分
• 創新點：4分

🧿 更多資料, 項目分享：

https://gitee.com/dancheng-senior/postgraduate

1 簡介

該設計學長使用python基于TensorFlow設計手寫數字識別算法，并編程實現GUI界面，構建手寫數字識別系統。

這是學長做的深度學習demo，大家可以用于畢業設計。

這里學長不會以論文的形式展現，而是以編程實戰完成深度學習項目的角度去描述。

項目要求：主要解決的問題是手寫數字識別，最終要完成一個識別系統。

設計識別率高的算法，實現快速識別的系統。

2 LeNet-5 模型的介紹

學長實現手寫數字識別，使用的是卷積神經網絡，建模思想來自LeNet-5，如下圖所示：

2.1 結構解析

這是原始的應用于手寫數字識別的網絡，我認為這也是最簡單的深度網絡。

LeNet-5不包括輸入，一共7層，較低層由卷積層和最大池化層交替構成，更高層則是全連接和高斯連接。

LeNet-5的輸入與BP神經網路的不一樣。這里假設圖像是黑白的，那么LeNet-5的輸入是一個32*32的二維矩陣。同
時，輸入與下一層并不是全連接的，而是進行稀疏連接。本層每個神經元的輸入來自于前一層神經元的局部區域(5×5)，卷積核對原始圖像卷積的結果加上相應的閾值，得出的結果再經過激活函數處理，輸出即形成卷積層（C層）。卷積層中的每個特征映射都各自共享權重和閾值，這樣能大大減少訓練開銷。降采樣層（S層）為減少數據量同時保存有用信息，進行亞抽樣。

2.2 C1層

第一個卷積層（C1層）由6個特征映射構成，每個特征映射是一個28×28的神經元陣列，其中每個神經元負責從5×5的區域通過卷積濾波器提取局部特征。一般情況下，濾波器數量越多，就會得出越多的特征映射，反映越多的原始圖像的特征。本層訓練參數共6×(5×5+1)=156個，每個像素點都是由上層5×5=25個像素點和1個閾值連接計算所得，共28×28×156=122304個連接。

2.3 S2層

S2層是對應上述6個特征映射的降采樣層（pooling層）。pooling層的實現方法有兩種，分別是max-pooling和mean-
pooling，LeNet-5采用的是mean-
pooling，即取n×n區域內像素的均值。C1通過2×2的窗口區域像素求均值再加上本層的閾值，然后經過激活函數的處理，得到S2層。pooling的實現，在保存圖片信息的基礎上，減少了權重參數，降低了計算成本，還能控制過擬合。本層學習參數共有1*6+6=12個，S2中的每個像素都與C1層中的2×2個像素和1個閾值相連，共6×(2×2+1)×14×14=5880個連接。

S2層和C3層連接

S2層和C3層的連接比較復雜。C3卷積層是由16個大小為10×10的特征映射組成的，當中的每個特征映射與S2層的若干個特征映射的局部感受野（大小為5×5）相連。其中，前6個特征映射與S2層連續3個特征映射相連，后面接著的6個映射與S2層的連續的4個特征映射相連，然后的3個特征映射與S2層不連續的4個特征映射相連，最后一個映射與S2層的所有特征映射相連。

此處卷積核大小為5×5，所以學習參數共有6×(3×5×5+1)+9×(4×5×5+1)+1×(6×5×5+1)=1516個參數。而圖像大小為28×28，因此共有151600個連接。

S4層是對C3層進行的降采樣，與S2同理，學習參數有16×1+16=32個，同時共有16×(2×2+1)×5×5=2000個連接。
C5層是由120個大小為1×1的特征映射組成的卷積層，而且S4層與C5層是全連接的，因此學習參數總個數為120×(16×25+1)=48120個。

2.4 F6與C5層

F6是與C5全連接的84個神經元，所以共有84×(120+1)=10164個學習參數。

卷積神經網絡通過通過稀疏連接和共享權重和閾值，大大減少了計算的開銷，同時，pooling的實現，一定程度上減少了過擬合問題的出現，非常適合用于圖像的處理和識別。

3 寫數字識別算法模型的構建

3.1 輸入層設計

輸入為28×28的矩陣，而不是向量。

3.2 激活函數的選取

Sigmoid函數具有光滑性、魯棒性和其導數可用自身表示的優點，但其運算涉及指數運算，反向傳播求誤差梯度時，求導又涉及乘除運算，計算量相對較大。同時，針對本文構建的含有兩層卷積層和降采樣層，由于sgmoid函數自身的特性，在反向傳播時，很容易出現梯度消失的情況，從而難以完成網絡的訓練。因此，本文設計的網絡使用ReLU函數作為激活函數。

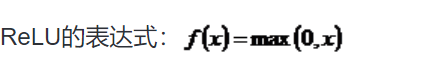
3.3 卷積層設計

學長設計卷積神經網絡采取的是離散卷積，卷積步長為1，即水平和垂直方向每次運算完，移動一個像素。卷積核大小為5×5。

3.4 降采樣層

學長設計的降采樣層的pooling方式是max-pooling，大小為2×2。

3.5 輸出層設計

輸出層設置為10個神經網絡節點。數字0~9的目標向量如下表所示：

4 網絡模型的總體結構

5 部分實現代碼

使用Python，調用TensorFlow的api完成手寫數字識別的算法。

注：我的程序運行環境是：Win10,python3.。

當然，也可以在Linux下運行，由于TensorFlow對py2和py3兼容得比較好，在Linux下可以在python2.7中運行。

?

#!/usr/bin/env python2# -*- coding: utf-8 -*-"""@author: 丹成學長 Q746876041"""#import modulesimport numpy as npimport matplotlib.pyplot as plt#from sklearn.metrics import confusion_matriximport tensorflow as tfimport timefrom datetime import timedeltaimport mathfrom tensorflow.examples.tutorials.mnist import input_datadef new_weights(shape):return tf.Variable(tf.truncated_normal(shape,stddev=0.05))def new_biases(length):return tf.Variable(tf.constant(0.1,shape=length))def conv2d(x,W):return tf.nn.conv2d(x,W,strides=[1,1,1,1],padding='SAME')def max_pool_2x2(inputx):return tf.nn.max_pool(inputx,ksize=[1,2,2,1],strides=[1,2,2,1],padding='SAME')#import datadata = input_data.read_data_sets("./data", one_hot=True) # one_hot means [0 0 1 0 0 0 0 0 0 0] stands for 2print("Size of:")print("--Training-set:\t\t{}".format(len(data.train.labels)))print("--Testing-set:\t\t{}".format(len(data.test.labels)))print("--Validation-set:\t\t{}".format(len(data.validation.labels)))data.test.cls = np.argmax(data.test.labels,axis=1)  # show the real test labels: [7 2 1 ..., 4 5 6], 10000valuesx = tf.placeholder("float",shape=[None,784],name='x')x_image = tf.reshape(x,[-1,28,28,1])y_true = tf.placeholder("float",shape=[None,10],name='y_true')y_true_cls = tf.argmax(y_true,dimension=1)# Conv 1layer_conv1 = {"weights":new_weights([5,5,1,32]),"biases":new_biases([32])}h_conv1 = tf.nn.relu(conv2d(x_image,layer_conv1["weights"])+layer_conv1["biases"])h_pool1 = max_pool_2x2(h_conv1)# Conv 2layer_conv2 = {"weights":new_weights([5,5,32,64]),"biases":new_biases([64])}h_conv2 = tf.nn.relu(conv2d(h_pool1,layer_conv2["weights"])+layer_conv2["biases"])h_pool2 = max_pool_2x2(h_conv2)# Full-connected layer 1fc1_layer = {"weights":new_weights([7*7*64,1024]),"biases":new_biases([1024])}h_pool2_flat = tf.reshape(h_pool2,[-1,7*7*64])h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat,fc1_layer["weights"])+fc1_layer["biases"])# Droupout Layerkeep_prob = tf.placeholder("float")h_fc1_drop = tf.nn.dropout(h_fc1,keep_prob)# Full-connected layer 2fc2_layer = {"weights":new_weights([1024,10]),"biases":new_weights([10])}# Predicted classy_pred = tf.nn.softmax(tf.matmul(h_fc1_drop,fc2_layer["weights"])+fc2_layer["biases"]) # The output is like [0 0 1 0 0 0 0 0 0 0]y_pred_cls = tf.argmax(y_pred,dimension=1) # Show the real predict number like '2'# cost function to be optimizedcross_entropy = -tf.reduce_mean(y_true*tf.log(y_pred))optimizer = tf.train.AdamOptimizer(learning_rate=1e-4).minimize(cross_entropy)# Performance Measurescorrect_prediction = tf.equal(y_pred_cls,y_true_cls)accuracy = tf.reduce_mean(tf.cast(correct_prediction,"float"))with tf.Session() as sess:init = tf.global_variables_initializer()sess.run(init)train_batch_size = 50def optimize(num_iterations):total_iterations=0start_time = time.time()for i in range(total_iterations,total_iterations+num_iterations):x_batch,y_true_batch = data.train.next_batch(train_batch_size)feed_dict_train_op = {x:x_batch,y_true:y_true_batch,keep_prob:0.5}feed_dict_train = {x:x_batch,y_true:y_true_batch,keep_prob:1.0}sess.run(optimizer,feed_dict=feed_dict_train_op)# Print status every 100 iterations.if i%100==0:# Calculate the accuracy on the training-set.acc = sess.run(accuracy,feed_dict=feed_dict_train)# Message for printing.msg = "Optimization Iteration:{0:>6}, Training Accuracy: {1:>6.1%}"# Print it.print(msg.format(i+1,acc))# Update the total number of iterations performedtotal_iterations += num_iterations# Ending timeend_time = time.time()# Difference between start and end_times.time_dif = end_time-start_time# Print the time-usageprint("Time usage:"+str(timedelta(seconds=int(round(time_dif)))))test_batch_size = 256def print_test_accuracy():# Number of images in the test-set.num_test = len(data.test.images)cls_pred = np.zeros(shape=num_test,dtype=np.int)i = 0while i < num_test:# The ending index for the next batch is denoted j.j = min(i+test_batch_size,num_test)# Get the images from the test-set between index i and jimages = data.test.images[i:j, :]# Get the associated labelslabels = data.test.labels[i:j, :]# Create a feed-dict with these images and labels.feed_dict={x:images,y_true:labels,keep_prob:1.0}# Calculate the predicted class using Tensorflow.cls_pred[i:j] = sess.run(y_pred_cls,feed_dict=feed_dict)# Set the start-index for the next batch to the# end-index of the current batchi = jcls_true = data.test.clscorrect = (cls_true==cls_pred)correct_sum = correct.sum()acc = float(correct_sum) / num_test# Print the accuracymsg = "Accuracy on Test-Set: {0:.1%} ({1}/{2})"print(msg.format(acc,correct_sum,num_test))# Performance after 10000 optimization iterationsoptimize(num_iterations=10000)print_test_accuracy()savew_hl1 = layer_conv1["weights"].eval()saveb_hl1 = layer_conv1["biases"].eval()savew_hl2 = layer_conv2["weights"].eval()saveb_hl2 = layer_conv2["biases"].eval()savew_fc1 = fc1_layer["weights"].eval()saveb_fc1 = fc1_layer["biases"].eval()savew_op = fc2_layer["weights"].eval()saveb_op = fc2_layer["biases"].eval()np.save("savew_hl1.npy", savew_hl1)np.save("saveb_hl1.npy", saveb_hl1)np.save("savew_hl2.npy", savew_hl2)np.save("saveb_hl2.npy", saveb_hl2)np.save("savew_hl3.npy", savew_fc1)np.save("saveb_hl3.npy", saveb_fc1)np.save("savew_op.npy", savew_op)np.save("saveb_op.npy", saveb_op)

運行結果顯示：測試集中準確率大概為99.2%。

查看混淆矩陣

6 在線手寫識別

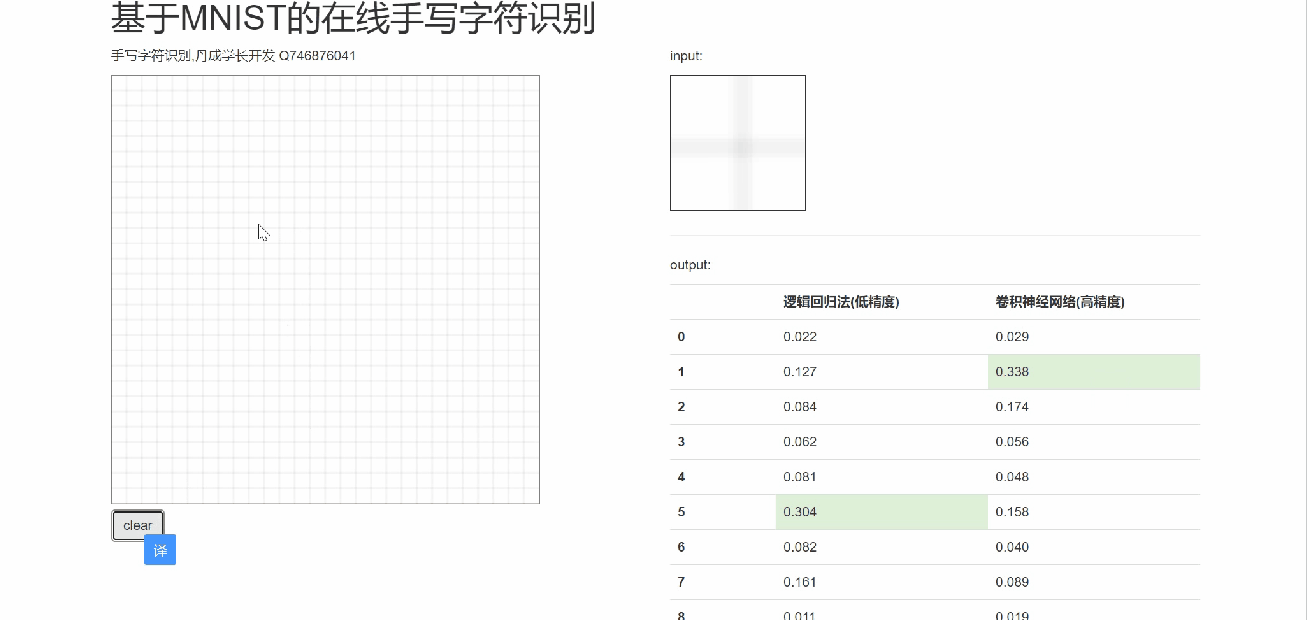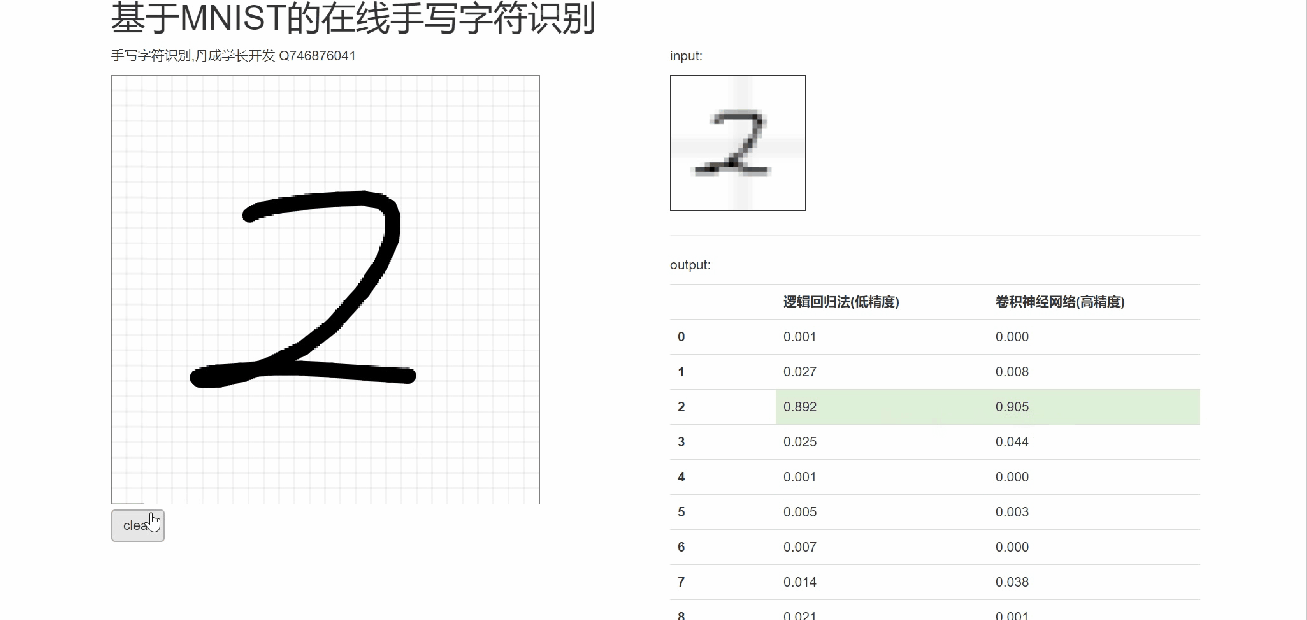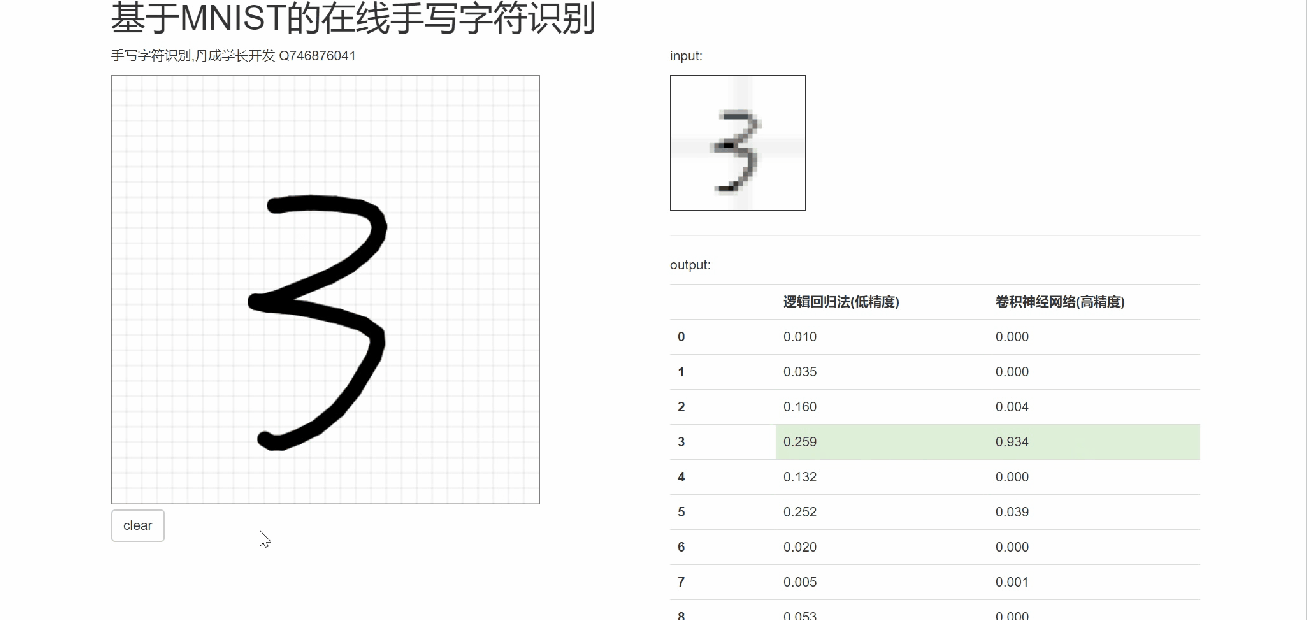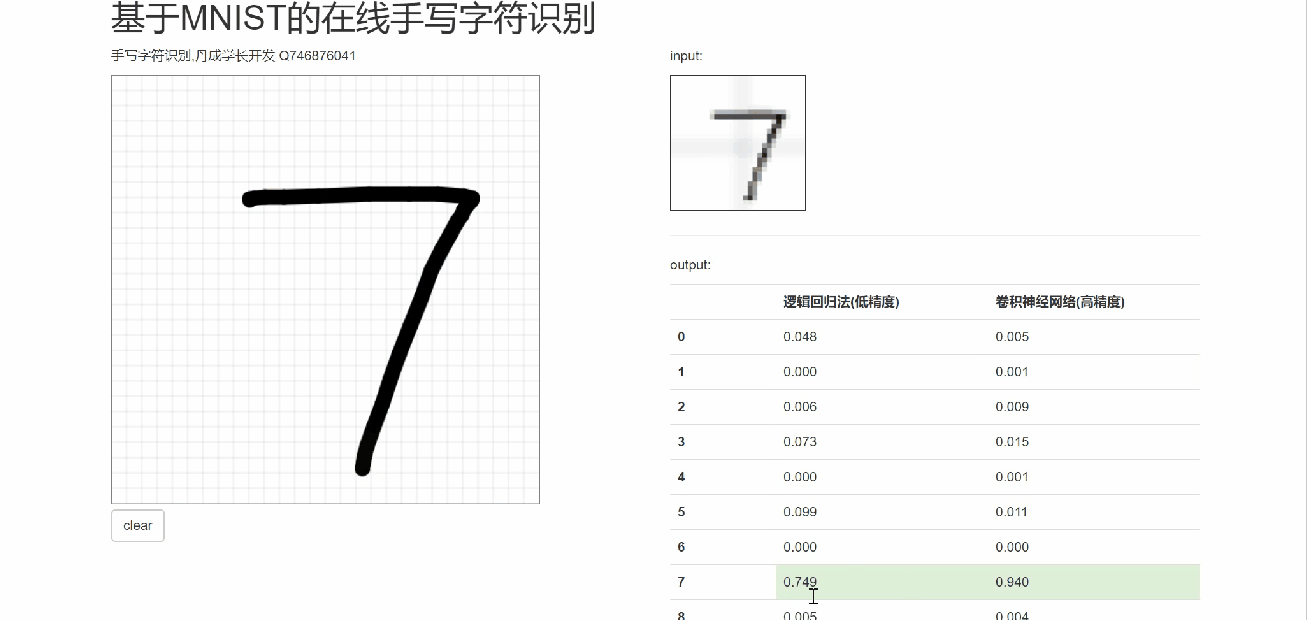
7 最后

🧿 更多資料, 項目分享：

https://gitee.com/dancheng-senior/postgraduate