本文為學習吳恩達版本機器學習教程的代碼整理,使用的數據集為https://github.com/fengdu78/Coursera-ML-AndrewNg-Notes/blob/f2757f85b99a2b800f4c2e3e9ea967d9e17dfbd8/code/ex1-linear%20regression/ex1data1.txt
將數據集和py代碼放到同一目錄中,使用Spyder打開運行,代碼中整體演示了數據加載處理過程、線性回歸損失函數計算方法、批量梯度下降方法、獲得結果后的預估方法、線性回歸結果函數繪制、模型導出及加載使用方法,其中最后三部分彼此無依賴關系可單獨執行。詳細代碼為下:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import joblib# 導入數據
path = 'ex1data1.txt'
data = pd.read_csv(path, header=None, names=['Population', 'Profit'])"""
計算線性回歸模型的損失值
"""
def computeCost(X, y, theta):"""此函數計算給定參數 theta 下的均方誤差損失。它用于評估線性回歸模型預測值與實際值之間的差異。損失值越小,表明模型的預測越準確。Parameters:X : numpy.ndarray 表示特征數據集的矩陣,其中包含了模型用于預測的特征。y : numpy.ndarray 表示目標變量的向量,包含了每個數據點的實際值。theta : numpy.ndarray 線性回歸模型的參數向量,包括截距項和特征的系數。Returns:float 返回計算得到的均方誤差損失值。"""# 計算模型預測值和實際值之間的差異inner = np.power(((X * theta.T) - y), 2)# 計算并返回均方誤差損失的平均值return np.sum(inner) / (2 * len(X))# 在數據集前面加入一列全為1的數據,用于適配截距項
data.insert(0, 'Ones', 1)# 分離特征(X)和目標變量(y)
cols = data.shape[1]
X = data.iloc[:,0:cols-1]#X是所有行,去掉最后一列
y = data.iloc[:,cols-1:cols]#X是所有行,最后一列# 將X和y的類型轉換為numpy矩陣,方便后續計算
X = np.matrix(X.values)
y = np.matrix(y.values)
theta = np.matrix(np.array([0,0]))# 初始化theta# 計算初始的損失值,僅為輸出和最終損失對比
initial_cost = computeCost(X, y, theta)
print("初始的損失值:", initial_cost)"""
執行批量梯度下降
"""
def gradientDescent(X, y, theta, alpha, iters):"""這個函數通過迭代地調整參數 theta,以最小化損失函數。Parameters:X : numpy.ndarray 特征數據集矩陣。y : numpy.ndarray 目標變量向量。theta : numpy.ndarray 線性回歸模型的初始參數向量。alpha : float 學習率,控制梯度下降的步長。iters : int 梯度下降的迭代次數。Returns:tuple 返回一個元組,包含優化后的 theta 和每次迭代的損失值數組。"""# 初始化一個臨時變量,用于更新 thetatemp = np.matrix(np.zeros(theta.shape))# 獲取 theta 中參數的數量parameters = int(theta.ravel().shape[1])# 初始化一個數組,用于記錄每次迭代的損失值cost = np.zeros(iters)# 迭代進行梯度下降for i in range(iters):# 計算當前參數下的誤差error = (X * theta.T) - y# 對每個參數進行更新for j in range(parameters):# 計算誤差與特征值的乘積term = np.multiply(error, X[:,j])# 更新 theta 的第 j 個參數temp[0,j] = theta[0,j] - ((alpha / len(X)) * np.sum(term))# 更新 thetatheta = temp# 記錄當前的損失值cost[i] = computeCost(X, y, theta)# 返回優化后的參數和損失值記錄return theta, cost# 設置學習率和迭代次數
alpha = 0.01
iters = 2000# 執行梯度下降算法,優化theta
g, cost = gradientDescent(X, y, theta, alpha, iters)# 計算優化后的損失值,僅為輸出和初始損失對比
final_cost = computeCost(X, y, g)
print("優化后的損失值", final_cost)"""
使用需要預測的數據X進行預測
"""
# 假設的人口數據
population_values = [3.5, 7.0] # 代表35,000和70,000人口# 對每個人口值進行預測
for pop in population_values:# 將人口值轉換為與訓練數據相同的格式(包括截距項)predict_data = np.matrix([1, pop]) # 添加截距項# 使用模型進行預測predict_profit = np.dot(predict_data, g.T)print(f"模型預測結果 {pop} : {predict_profit[0,0]}")"""
使用模型繪制函數
"""
# 創建預測函數
x = np.linspace(data.Population.min(), data.Population.max(), 100)
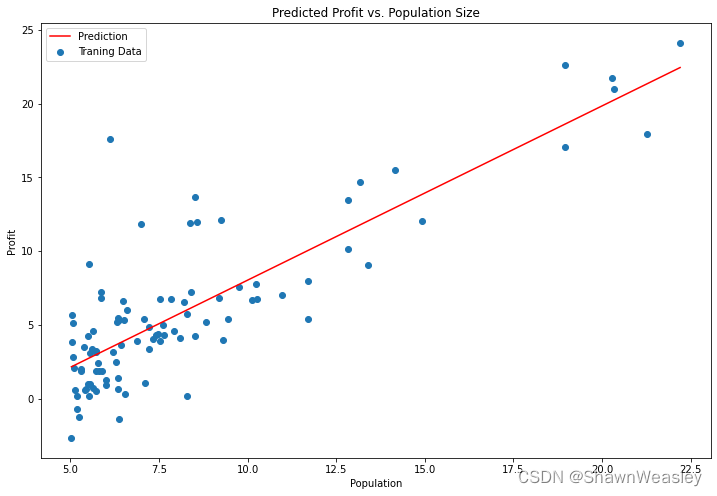
f = g[0, 0] + (g[0, 1] * x)# 繪制線性回歸結果
fig, ax = plt.subplots(figsize=(12,8))
ax.plot(x, f, 'r', label='Prediction')# 繪制預測線
ax.scatter(data.Population, data.Profit, label='Traning Data')# 繪制訓練數據點
ax.legend(loc=2)
ax.set_xlabel('Population')
ax.set_ylabel('Profit')
ax.set_title('Predicted Profit vs. Population Size')
plt.show()"""
使用模型繪制損失值變化曲線
"""
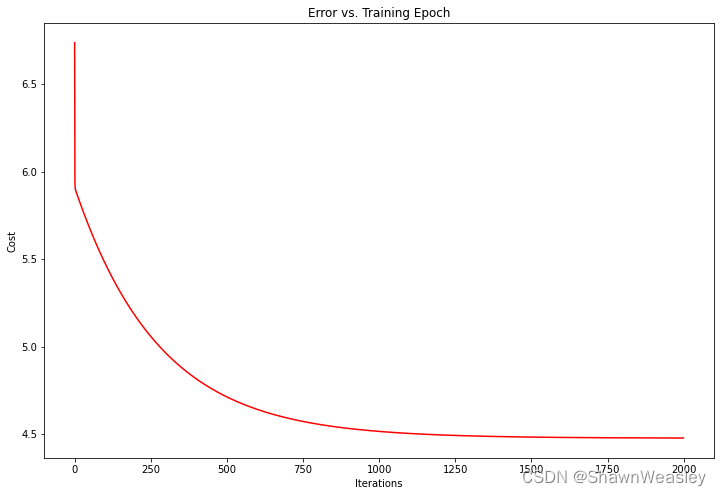
# 繪制損失函數的變化
fig, ax = plt.subplots(figsize=(12,8))
ax.plot(np.arange(iters), cost, 'r') # 損失值隨迭代次數的變化
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title('Error vs. Training Epoch')
plt.show()"""
保存模型
"""
# 保存模型
joblib.dump(g, 'linear_regression_model.pkl')"""
加載模型并執行預測
"""
# 加載模型
loaded_model = joblib.load('linear_regression_model.pkl')# 假設的人口數據
population_values = [3.5, 7.0] # 代表35,000和70,000人口# 使用模型進行預測
for pop in population_values:# 更新預測數據矩陣,包括當前的人口值predict_data = np.matrix([1, pop])# 進行預測predict_value = np.dot(predict_data, loaded_model.T)print(f"加載模型預測結果 {pop} : {predict_value[0,0]}")
運行后結果:
輸出結果:
初始的損失值: 32.072733877455676
優化后的損失值 4.47802760987997
模型預測結果 3.5 : 0.349676138927709
模型預測結果 7.0 : 4.487420850578528
加載模型預測結果 3.5 : 0.349676138927709
加載模型預測結果 7.0 : 4.487420850578528

)

?它的作用是什么?)






之LC濾波器的基礎知識)






(展示自己的地圖瓦片)3.0版本api)

