數據結構之----原碼、反碼、補碼
什么是原碼?
原碼:我們將數字的二進制表示的最高位視為符號位,其中 0 表示正數,1 表示負數,其余位表示數字
的值。
什么是反碼?
反碼:正數的反碼與其原碼相同,負數的反碼是對其原碼除符號位外的所有位取反。
什么是補碼?
補碼:正數的補碼與其原碼相同,負數的補碼是在其反碼的基礎上加 1 。
下圖是原碼、反碼和補碼之間的轉換方法。
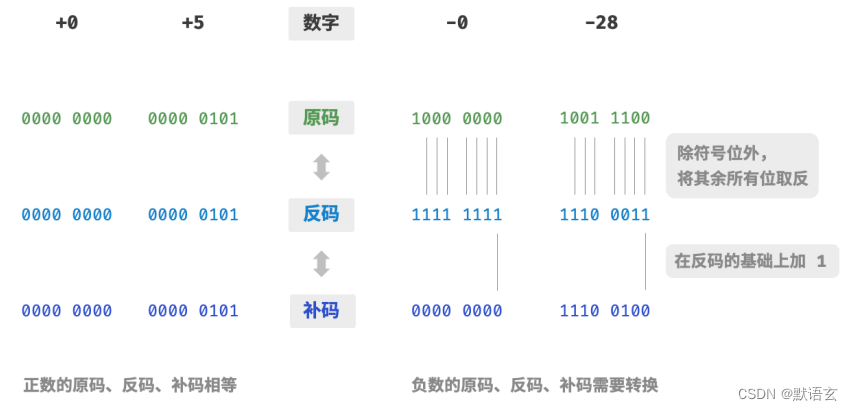
為什么要使用原碼?
眾所周知,計算機所能讀懂的語言是二進制編碼,而二進制編碼就是我們這里所說的原碼。
為什么要使用反碼?
原碼雖然說很直觀,但是它也會存在一些局限性。如,負數的原碼是不能直接的用于運算的。
例:1+(-2),得到的結果是 -3 并不是 -1,這明顯是錯誤的。

所以,為了解決這類問題,計算機引入了反碼。如果說我們先將原碼轉為反碼,在計算完1+(-2)后,再將結果轉換為原碼,那么得出的就是正確的結果 -1。

為什么要使用補碼?
在原碼中,我們都知道數字零有兩種表達方式+0 和 ?0 ,但是這意味著0是兩個不同的二進制編碼,它可能會帶來歧義。如在判斷條件中,如果沒有正確區分 +0和- 0,就會導致判斷錯誤。
而如果需要正確的對0進行區分就要進行額外的操作,但是這種操作可能會降低計算機的效率。
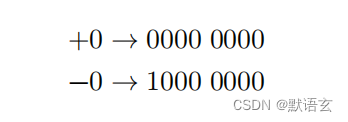
并且反碼和原碼一樣,也會存在這個問題,所以為了解決這個問題,計算機引入了補碼。
下面是負零的原碼、反碼、補碼的轉換過程:
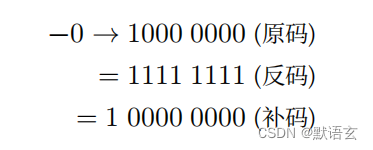
轉換原理是在反碼的基礎上加一,而加一這個操作會產生進位,但是byte類型的長度只有8bite,所以溢出的第九位的 1會被舍棄。
也就是說 負零的補碼為 0000 0000 ,與正零的補碼相同。這意味著在補碼表示中只存在一個零,
正負零歧義從而得到解決。
為什么byte的取值區間為[-128,+127]?
我們注意到,區間 [?127, +127] 內的所有整數都有對應的原碼、反碼和補碼,并且原碼和補碼之間是可以互相轉換的。然而,補碼 1000 0000 是一個例外,它并沒有對應的原碼。
根據上面提到的轉換方法我們可以算出 1000 0000的原碼是 0000 0000。
這顯然是不對的,因為該原碼表示數字 0 ,它的補碼應該是自身 0。
所以計算機將這個特殊的補碼 1000 0000 代表 -128
實際上,(?1) + (?127) 在補碼下的計算結果就是 ?128 。

--情報搜集階段)

)



)

)




)




)
