【算法系列篇】遞歸、搜索和回溯（二）

在這里插入圖片描述

文章目錄

前言
1. 兩兩交換鏈表中的節點
- 1.1 題目要求
- 1.2 做題思路
- 1.3 代碼實現
2. Pow(X,N)
- 2.1 題目要求
- 2.2 做題思路
- 2.3 代碼實現
3. 計算布爾二叉樹的值
- 3.1 題目要求
- 3.2 做題思路
- 3.3 代碼實現
4. 求根節點到葉結點數字之和
- 4.1 題目要求
- 4.2 做題思路
- 4.3 代碼實現

前言

前面為大家介紹了關于遞歸的知識，以及使用遞歸解決了幾個問題，那么這篇文章將帶大家鞏固一下關于遞歸的知識。

1. 兩兩交換鏈表中的節點

https://leetcode.cn/problems/swap-nodes-in-pairs/description/

1.1 題目要求

給你一個鏈表，兩兩交換其中相鄰的節點，并返回交換后鏈表的頭節點。你必須在不修改節點內部的值的情況下完成本題（即，只能進行節點交換）。

示例 1：
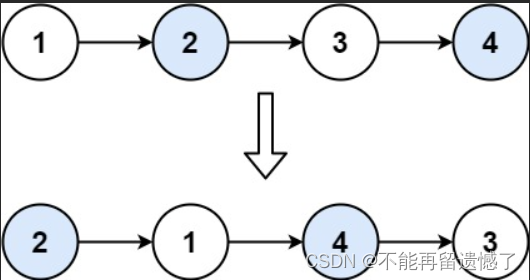
在這里插入圖片描述

輸入：head = [1,2,3,4]
輸出：[2,1,4,3]

示例 2：

輸入：head = []
輸出：[]

示例 3：

輸入：head = [1]
輸出：[1]

提示：

鏈表中節點的數目在范圍 [0, 100] 內
0 <= Node.val <= 100

/*** Definition for singly-linked list.* public class ListNode {*     int val;*     ListNode next;*     ListNode() {}*     ListNode(int val) { this.val = val; }*     ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
class Solution {public ListNode swapPairs(ListNode head) {}
}

1.2 做題思路

這道題目其實可以使用非遞歸的方式來實現，但是我們可以使用遞歸的方式來加深一下遞歸的學習。

這個題目不復雜，比較簡單，我們可以將 head 和 head.next 看成一部分，另外的節點看成另一部分，開始我們直接將后面部分的節點交給函數處理，相信它一定可以幫助我們完成兩兩節點的交換，當后面部分的節點交換完成之后，我們再交換 head 和 head.next 節點，然后再將這兩個部分連接起來。

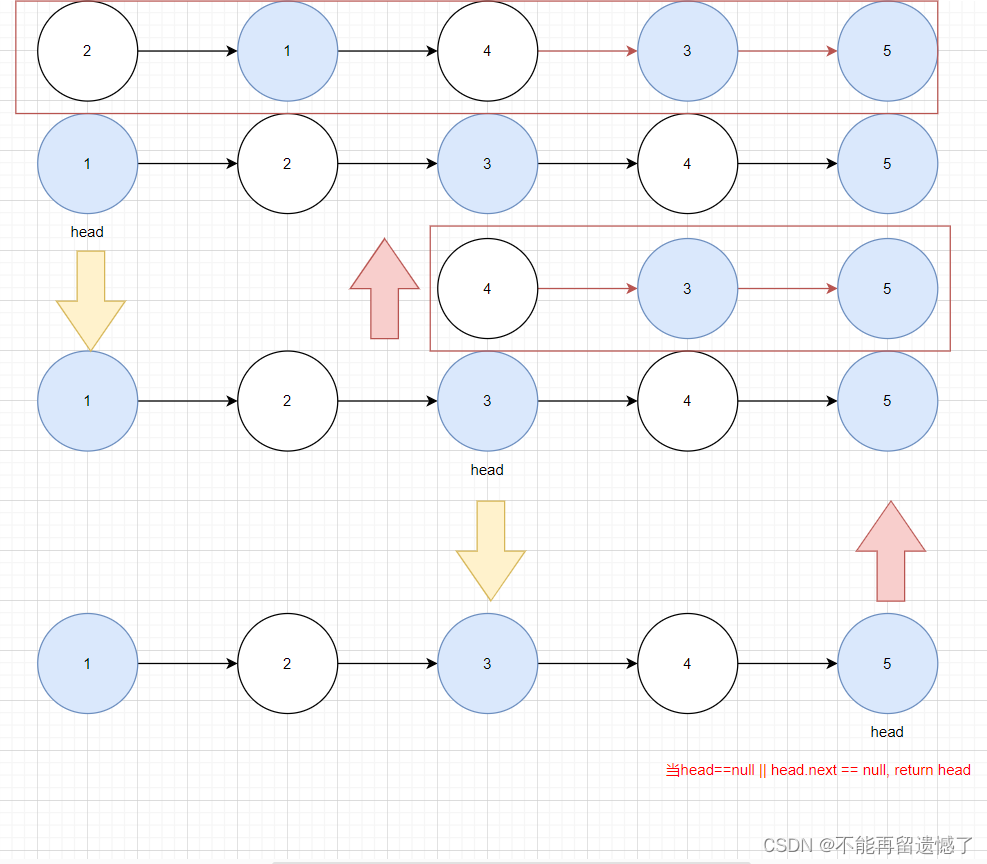
在這里插入圖片描述

這是一種思路，我們也可以先交換前面部分，然后再交換后面部分。

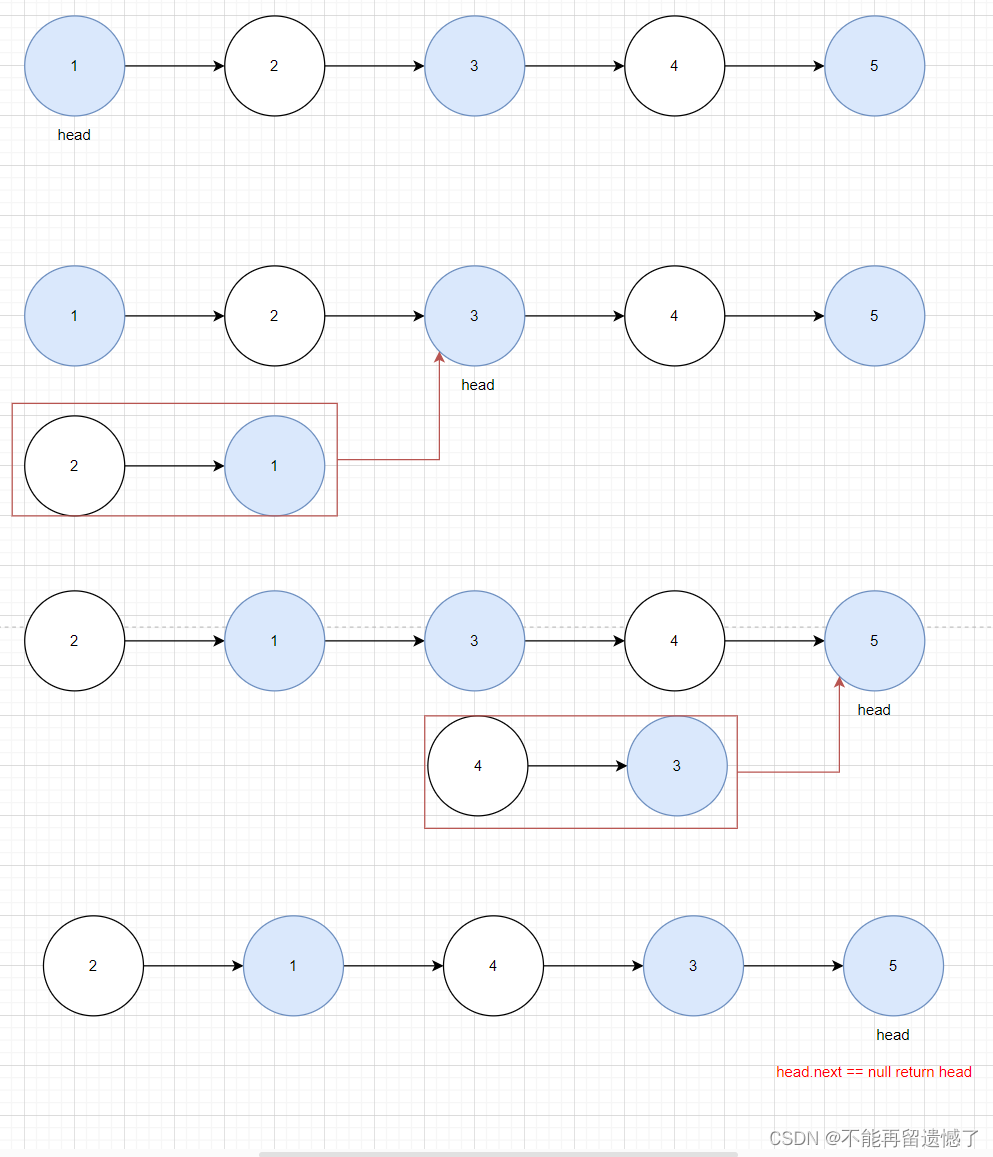
在這里插入圖片描述

上面兩種思路其實都差不多的，只是先交換還是后交換的區別。

1.3 代碼實現

/*** Definition for singly-linked list.* public class ListNode {*     int val;*     ListNode next;*     ListNode() {}*     ListNode(int val) { this.val = val; }*     ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
class Solution {public ListNode swapPairs(ListNode head) {if (head == null || head.next == null) return head;ListNode l1 = swapPairs(head.next.next);ListNode ret = head.next;head.next.next = head;head.next = l1;return ret;}
}

在這里插入圖片描述

/*** Definition for singly-linked list.* public class ListNode {*     int val;*     ListNode next;*     ListNode() {}*     ListNode(int val) { this.val = val; }*     ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
class Solution {public ListNode swapPairs(ListNode head) {if (head == null || head.next == null) return head;ListNode curNext = head.next.next;ListNode ret = head.next;head.next.next = head;head.next = swapPairs(curNext);return ret;}
}

在這里插入圖片描述

2. Pow(X,N)

https://leetcode.cn/problems/powx-n/

2.1 題目要求

實現 pow(x, n) ，即計算 x 的整數 n 次冪函數（即，xn ）。

示例 1：

輸入：x = 2.00000, n = 10
輸出：1024.00000

示例 2：

輸入：x = 2.10000, n = 3
輸出：9.26100

示例 3：

輸入：x = 2.00000, n = -2
輸出：0.25000
解釋：2-2 = 1/22 = 1/4 = 0.25

提示：

-100.0 < x < 100.0
-231 <= n <= 231-1
n 是一個整數
要么 x 不為零，要么 n > 0 。
-104 <= xn <= 104

class Solution {public double myPow(double x, int n) {}
}

2.2 做題思路

其實這道題也叫做快速冪，為什么叫做快速冪呢？給大家舉個例子：假設我們要求2^8，普通的做法就是2x2x2x2x2x2x2x2，但是呢？2 ^ 8可以寫成 2 ^ 4 x 2 ^ 4，而 2 ^ 4 又可以寫成 2 ^ 2 x 2 ^ 2，2 ^ 2可以寫成 2 x 2，2 可以寫成 1 x 2。也就是說 2 ^ n 可以寫成 2 ^ (n / 2) x 2 ^ (n / 2)，我們每次只需要計算 2 ^ (n / 2) 的值及，就可以了，通過這種快速冪的方法，就可以大大節省計算的時間。

當冪為偶數的話就可以每次求 x 的 n / 2 次冪，但是如果冪數為奇數該怎么辦呢？這也不復雜，當冪數為奇數的時候，我們只需要在 n / 2 次冪 x n / 2 次冪后面在乘上一個 x 就可以了。舉個例子：2 ^ 5就可以寫成 2 ^ 2 x 2 ^ 2 x 2。

2.3 代碼實現

class Solution {public double myPow(double x, int n) {//處理冪數的正負問題if (n < 0) return 1.0 / quickPow(x, n);else return quickPow(x, n);}private double quickPow(double x, int n) {if (n == 0) return 1.0;double t = quickPow(x, n / 2);//處理冪數的奇偶問題return n % 2 == 0 ? t * t : t * t * x;}
}

在這里插入圖片描述

3. 計算布爾二叉樹的值

https://leetcode.cn/problems/evaluate-boolean-binary-tree/

3.1 題目要求

給你一棵完整二叉樹的根，這棵樹有以下特征：

葉子節點要么值為 0 要么值為 1 ，其中 0 表示 False ，1 表示 True 。
非葉子節點要么值為 2 要么值為 3 ，其中 2 表示邏輯或 OR ，3 表示邏輯與 AND

計算一個節點的值方式如下：

如果節點是個葉子節點，那么節點的值為它本身，即 True 或者 False 。
否則，計算兩個孩子的節點值，然后將該節點的運算符對兩個孩子值進行運算。
返回根節點 root 的布爾運算值。

完整二叉樹是每個節點有 0 個或者 2 個孩子的二叉樹。

葉子節點是沒有孩子的節點。

示例 1：
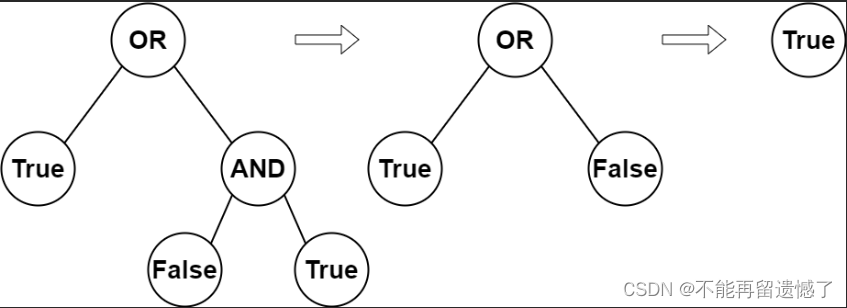
在這里插入圖片描述

輸入：root = [2,1,3,null,null,0,1]
輸出：true
解釋：上圖展示了計算過程。
AND 與運算節點的值為 False AND True = False 。
OR 運算節點的值為 True OR False = True 。
根節點的值為 True ，所以我們返回 true 。

示例 2：

輸入：root = [0]
輸出：false
解釋：根節點是葉子節點，且值為 false，所以我們返回 false 。

提示：

樹中節點數目在 [1, 1000] 之間。
0 <= Node.val <= 3
每個節點的孩子數為 0 或 2 。
葉子節點的值為 0 或 1 。
非葉子節點的值為 2 或 3 。

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public boolean evaluateTree(TreeNode root) {}
}

3.2 做題思路

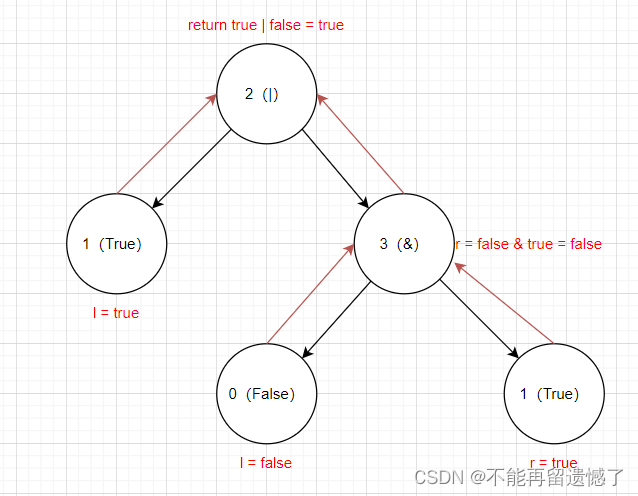
這道題目的意思就是如果遇到的節點是一個葉子節點的話，如果當前節點的值為0的話就返回False，為1的話就返回True；如果當前節點不是葉子節點的話，就需要根據這個節點的父親節點的值與這個節點的兄弟節點進行操作，如果父親節點是2的話，就進行 | 操作，3就進行 & 操作。

一般遇到二叉樹就會想到遞歸，這道題也不例外。我們先將根節點的左樹交給函數，讓函數幫助我們進行布爾值的計算，然后再將根節點的右樹交給函數進行布爾值的運算，最后將左右子樹的值與根節點表示的值進行 | 或者 & 運算。

在這里插入圖片描述

3.3 代碼實現

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public boolean evaluateTree(TreeNode root) {//當root為null時返回trueif (root == null) return true;//遇到葉子節點根據節點的值返回if (root.left == null && root.right == null) {if (root.val == 0) return false;else return true;}boolean l = evaluateTree(root.left);boolean r = evaluateTree(root.right);if (root.val == 2) return l | r;else return l & r;}
}

在這里插入圖片描述

4. 求根節點到葉結點數字之和

https://leetcode.cn/problems/sum-root-to-leaf-numbers/

4.1 題目要求

給你一個二叉樹的根節點 root ，樹中每個節點都存放有一個 0 到 9 之間的數字。
每條從根節點到葉節點的路徑都代表一個數字：

例如，從根節點到葉節點的路徑 1 -> 2 -> 3 表示數字 123 。
計算從根節點到葉節點生成的所有數字之和。

葉節點是指沒有子節點的節點。

示例 1：
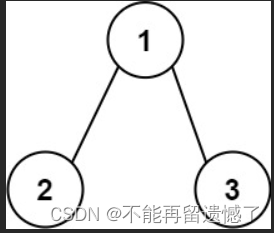
在這里插入圖片描述

輸入：root = [1,2,3]
輸出：25
解釋：
從根到葉子節點路徑 1->2 代表數字 12
從根到葉子節點路徑 1->3 代表數字 13
因此，數字總和 = 12 + 13 = 25

示例 2：

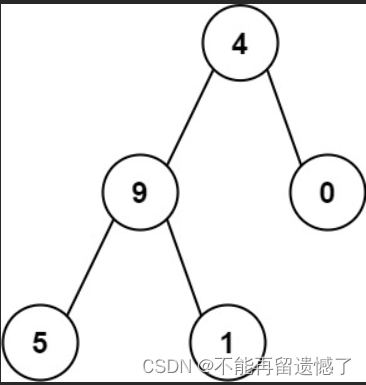
在這里插入圖片描述

輸入：root = [4,9,0,5,1]
輸出：1026
解釋：
從根到葉子節點路徑 4->9->5 代表數字 495
從根到葉子節點路徑 4->9->1 代表數字 491
從根到葉子節點路徑 4->0 代表數字 40
因此，數字總和 = 495 + 491 + 40 = 1026

提示：

樹中節點的數目在范圍 [1, 1000] 內
0 <= Node.val <= 9
樹的深度不超過 10

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public int sumNumbers(TreeNode root) {}
}

4.2 做題思路

這道題目也不難，只要能理解二叉樹的的前序遍歷就可以了，這道題目其實就是二叉樹的前序遍歷。我們先將根節點的左子樹交給函數得到左子樹上從根節點到各個葉子節點路徑上的數字之和，然后將根節點的右子樹上的從根節點到各個葉子節點路徑上的數字之和，然后返回左子樹和右子樹返回值的和。

4.3 代碼實現

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public int sumNumbers(TreeNode root) {return dfs(root, 0);}//n用來記錄當前路徑上該節點之前的各個節點的和private int dfs(TreeNode root, int n) {if (root == null) return 0;//遇到一個節點就將當前節點的值加在n上n = n * 10 + root.val;//遇到葉子節點就說明當前節點的值計算完成，就返回路徑上所以數字和if (root.left == null && root.right == null) return n;//分別計算根節點左右子樹上根節點到葉子節點路徑上數字和int l = dfs(root.left, n);int r = dfs(root.right, n);//返回左子樹和右子樹所有路徑上數字和return l + r;}
}