本系列根據國外一個圖形小哥的講解為本，整合互聯網的一些資料，結合自己的一些理解。

場景的組成部分

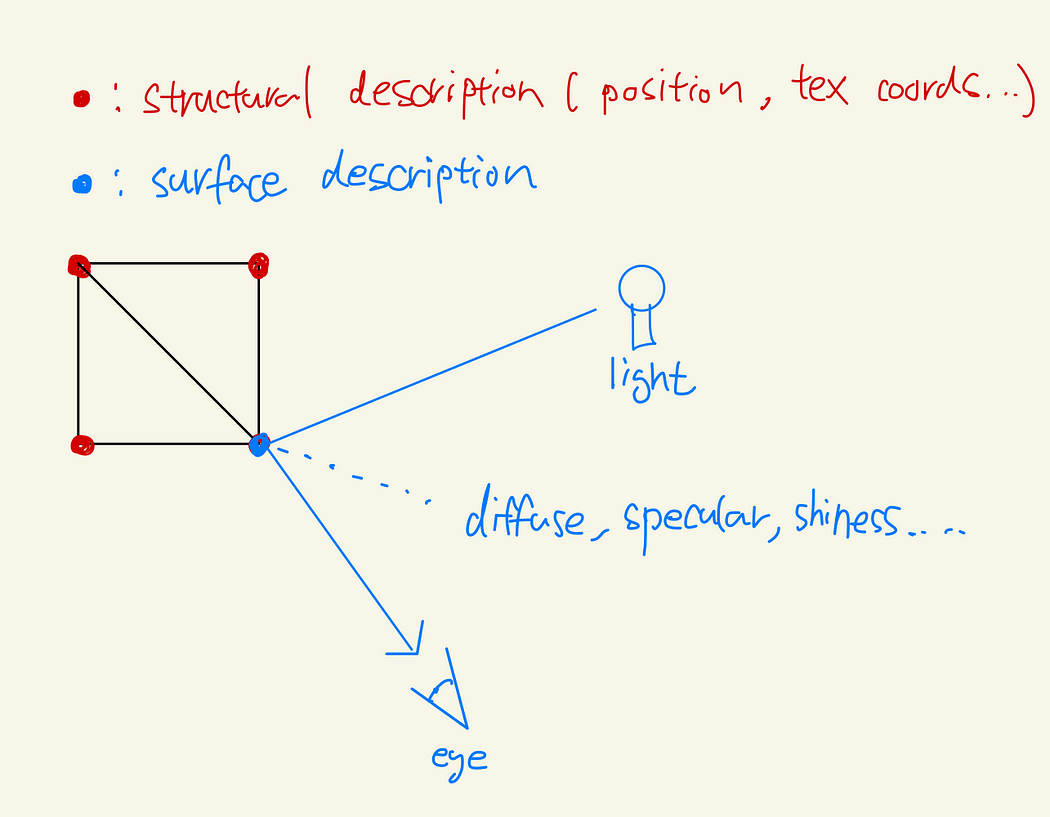
場景相當于一個或多個模型的集合。模型包含以下內容：

• 結構描述：幾何形狀，如頂點、紋理坐標等
• 表面描述：外觀及光照等

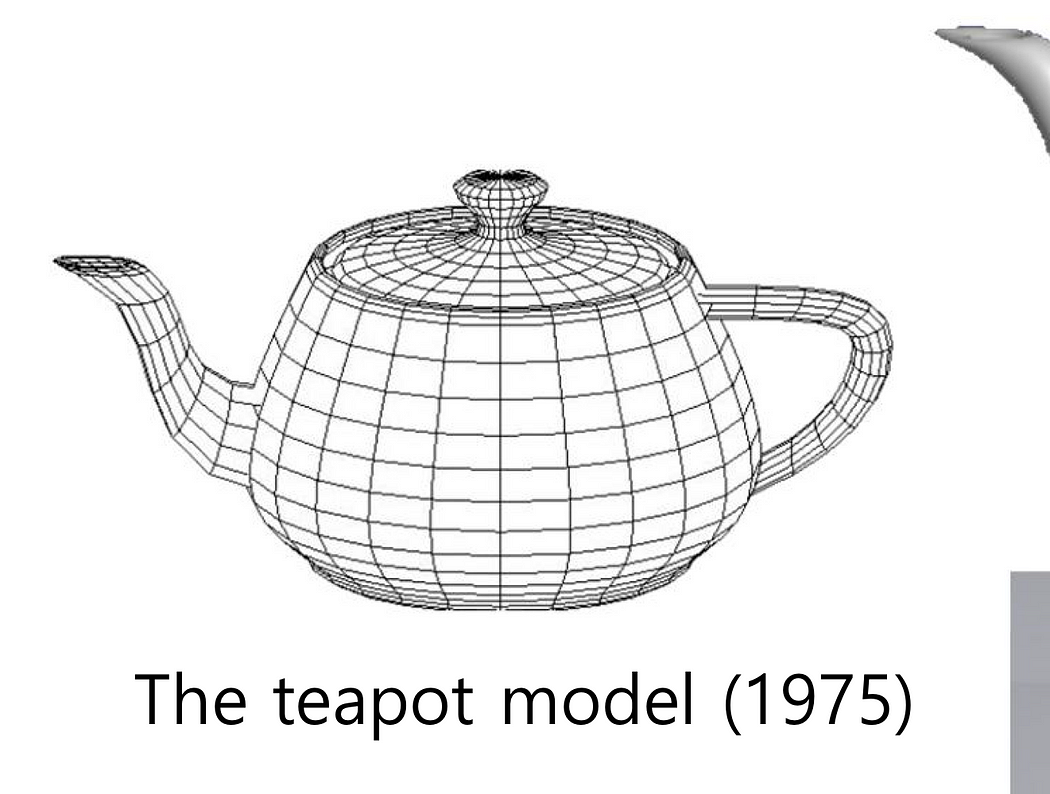
猶他壺模型（Utah teapot）

對于學圖形學的人來說，猶他壺并不陌生。猶他壺模型是計算機圖形學早期著名的3D模型（大約70年代~80年代）。在那個時候，3D模型通常被表示為多項式函數，主要技術被稱為“樣條曲線（spline curves）”，該技術將模型劃分為多個表面塊，如下所示：

三角形網格

現在我們主要使用多邊形或三角形網格來構建模型。

3D 對象數據的類型

• 多邊形網格（polygonal meshes） —— 代表復雜的現實世界對象。
• 樣條面片（spline patches） —— 程序化建模。
• 體積數據，體素（voxel） —— 通過將對象的密度存儲在三維數組中來表示對象。
• 構造立體幾何（Constructive Solid Geometry） —— 常用于機器零件。
• 其他。

這是網格和樣條線之間的比較：

建模技術

點云技術

首先，點云樣本是非結構化的數據，所以沒有關于兩點之間鄰接（連通性）的信息。為了使點能夠連接在一起，我們必須使用額外的算法，例如 K 最近鄰算法。

使用點云技術的優點之一是“簡單”。此外，由于點云樣本通過掃描能成為“原始數據raw data”，因此如今備受關注。

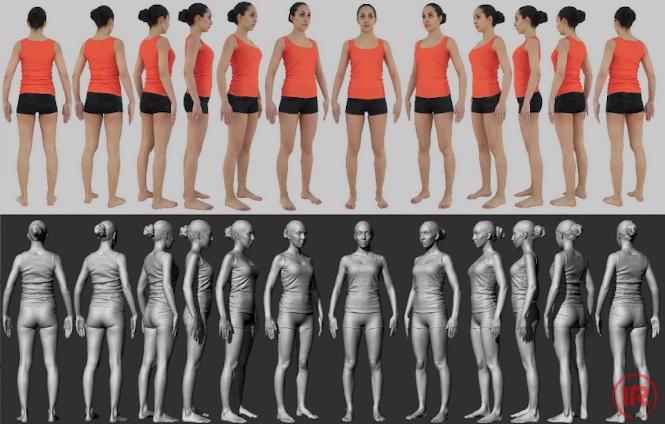
使用相機進行 3D 掃描

原理是通過一系列相機掃描物體，之后相機生成點云并捕獲紋理。

原始數據都是“rgbd”數據，“rgb”的部分用于表示顏色和紋理，然后“d”（深度）用于生成點云。深度是指點與相機之間的距離。

多邊形湯（Polygon Soup）

多邊形湯是一組非結構化的多邊形。它可以渲染一個對象，但不可以再進行其他操作，因為這些多邊形之間并沒有幾何上的連系，也不含拓撲信息。為什么起這個名可以看下知乎的一個回答。

網格（Mesh）

網格是一組連接的多邊形（通常是三角形）。 例如，多邊形可以由多個三角形組成，并且三角形表示為一組頂點。一開始三角形之間沒有連接，我們可以通過為每個頂點附加有關相鄰三角形的附加信息（索引）來實現多邊形上的連接。

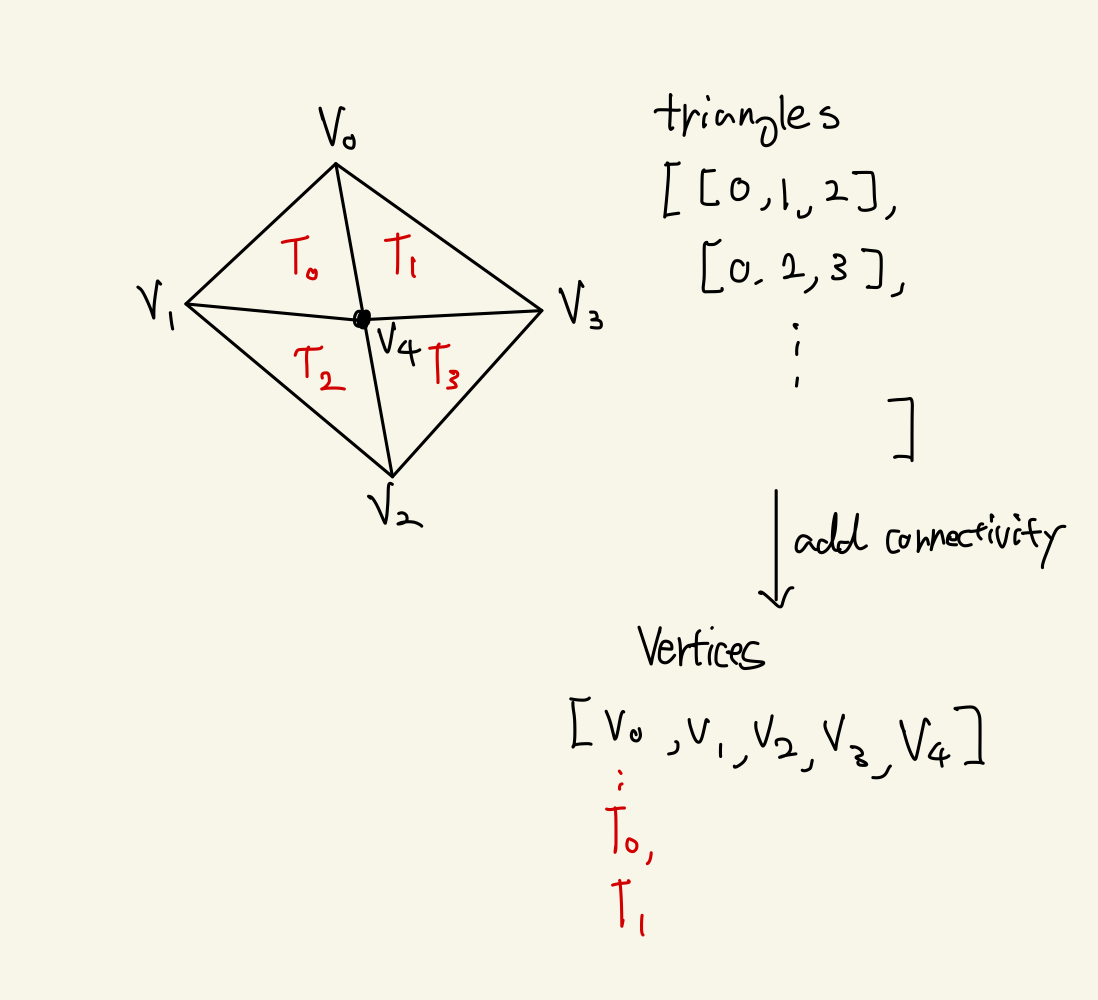
網格是表示對象的顯式方法。

隱式曲面（水平集 Level set）

通過使用三維函數，我們可以隱式地表示一個對象。曲面表面上的點應滿足“F(x,y,z) = 0”。當函數的結果為零時，表示該點是曲面上的一個點，稱為等值曲面。

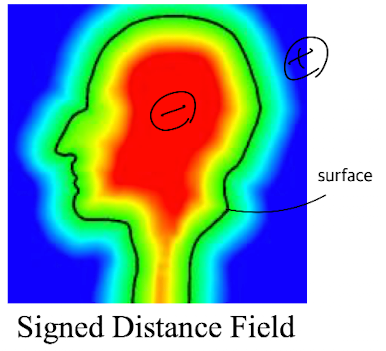
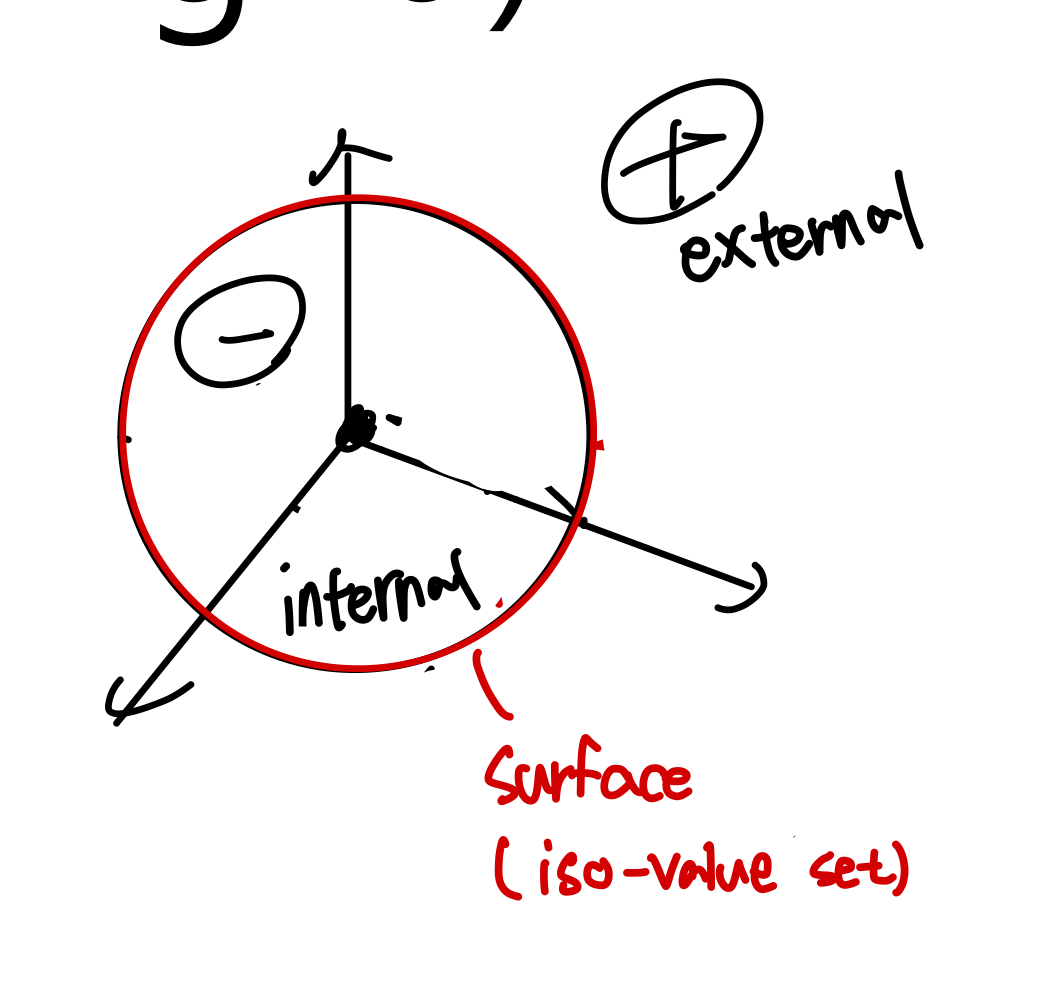
這種技術有優點也有缺點。
優點：

• 可以保證模型無孔洞
• 易于改變拓撲

缺點：

• 必須遍歷體積數據，就會造成 CPU 時間開銷，導致速度慢。
• 需要更多的內存空間。

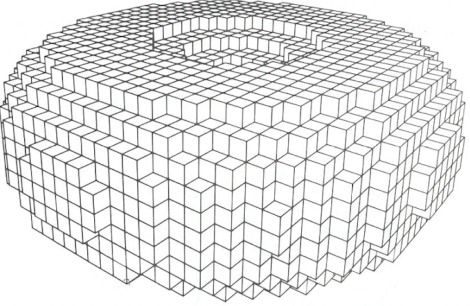
體素（Voxels）

醫療領域在CT、MRI中經常使用此類物體。體素是體積數據的 3D 圖像。

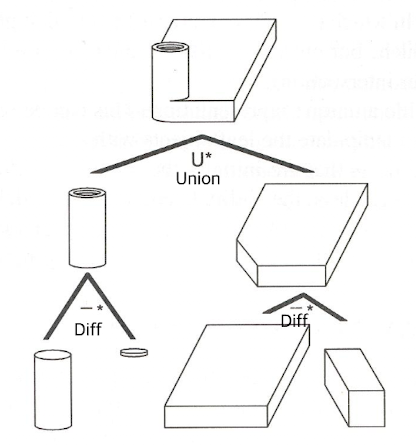
構造立體幾何

使用主要的幾何圖形，從布爾運算的層次結構中獲得目標幾何圖形（并集、差集和交集），例子之一是CAD程序中的機械建模。

場景圖（Scene Graph）

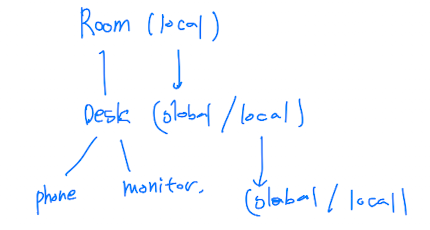
文章的開頭提到過“一個場景相當于一個或多個模型的組合”。我們可以將模型放置為層次樹，而不是將它們放置為列表。

如下圖所示，從辦公桌的角度來看，桌面上的一組模型（電話、鏡子、相框）是葉子節點。通過使它們依賴于辦公桌，我們可以構建新的模型。

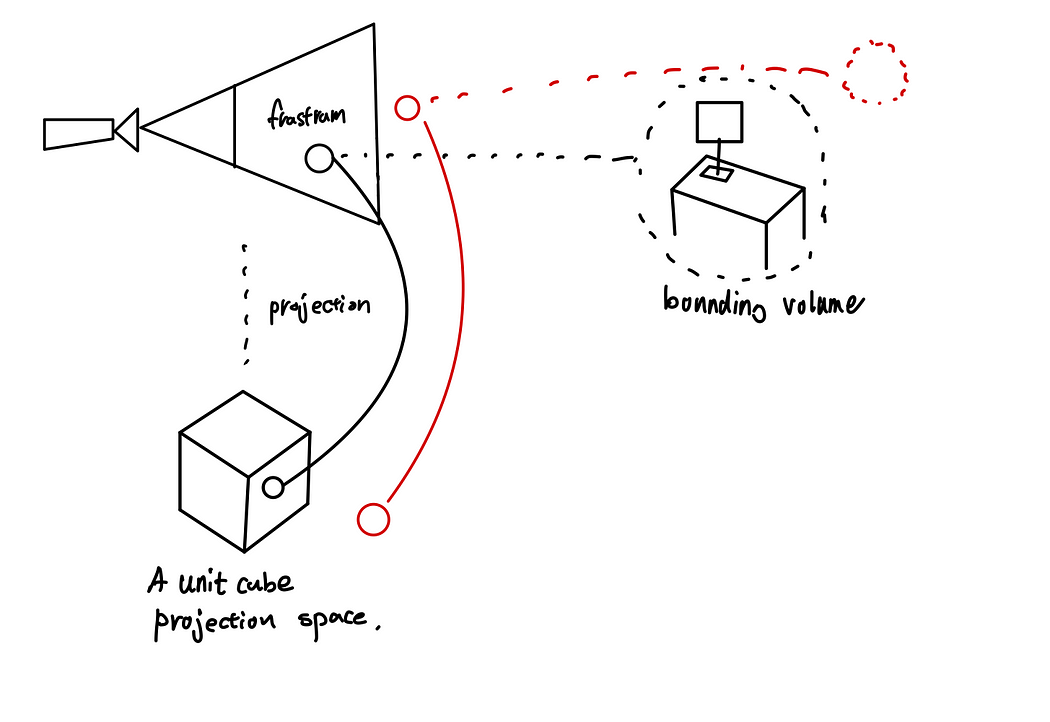
通過繪制一組對象的圖形，我們可以應用視椎體進行剔除。“視錐體”是相機能夠看到物體的空間。“剔除”是一種不會在視錐體空間之外渲染對象的技術。創建一組模型后，我們可以為包含所有對象的組設置包圍體。如果我們將視圖空間投影到單位立方體空間（NDC空間），紅球將位于該空間之外。然后，我們可以在 CPU 操作內將其從渲染目標中刪除。

程序化建模

我們在這里使用替換規則。

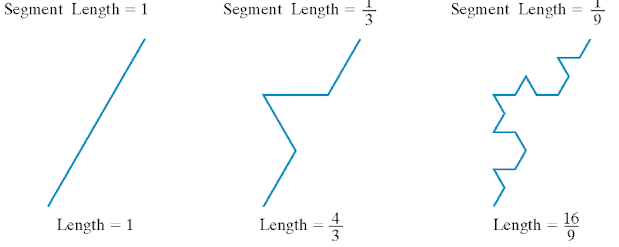
程序化建模的一個例子是“地形”。我們不使用純隨機數，而是利用高度圖并生成受相鄰位置高度影響的隨機數。