本部分視頻所在地址：深度強化學習的理論與實踐

2.1節 動態規劃簡介

態規劃有兩種思路：分治法和動態規劃，目的是求解一個大問題。
分治法
分治法是將一個大問題分解成多個相互獨立的子問題。然后再逐個解決每個子問題，最后將多個問題的結算結果c1、c2、…、cn進行總結，最后得到總問題的解。
subp1:表示將大問題分成的子問題
這些子問題的特點是這些子問題之間是相互獨立的，也就是這些子問題是可以獨立求解的。
動態規劃
這個方法是將一個總問題進行逐步求解，先求解subp1，再求解subp2，…，最后求解subpn問題，
子問題的特點是嵌套的，遞歸的求解，即想要解決子問題subp3，必須先要求解子問題subp2，想要解決子問題subp2，必須先要求解子問題subp1。每個子問題的結構是一樣的，即如果一個子問題是加法問題，則所有問題都是加法問題。

找到的其結構特征，就是去找到嵌套的結構特征

動態規劃解決問題的案例

2.2節 值函數與貝爾曼方程

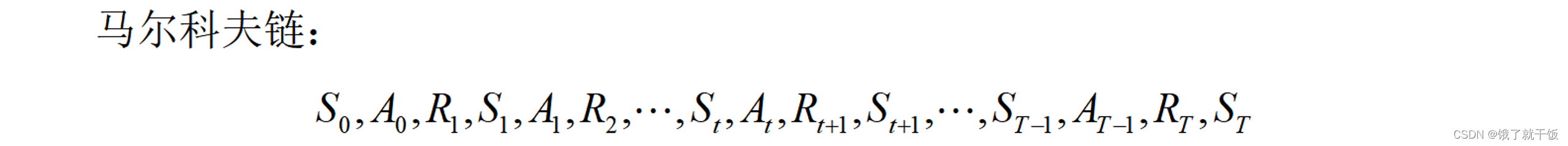
根據馬爾科夫鏈定義一些東西：
即時獎勵（通常稱為獎勵，reward）
累計獎勵Gt: 表示狀態為St時執行動作At之后累積的獎勵。累計獎勵中每一個時刻對應的即時獎勵不能夠同等看待。原因是例如在下象棋時第一步走馬和棋局最后幾步走馬同樣是走馬的動作，但是走馬的動作重要性是不同的。所得到的即時獎勵是不同的。在棋局最后的終止狀態附近的獎勵應該被認為是更重要的。
累積折扣獎勵（通常稱回報，return）： 智能體在t時刻的累積獎勵會這么認為，離該時刻越近的即時獎勵重要性應該越大，離該時刻越遠的即時獎勵重要性越小。舉例：在終止狀態T時刻，RT的重要性要遠超于R1的重要性，其根本原因是動作AT-1的重要性要遠超于動作A0的重要性。

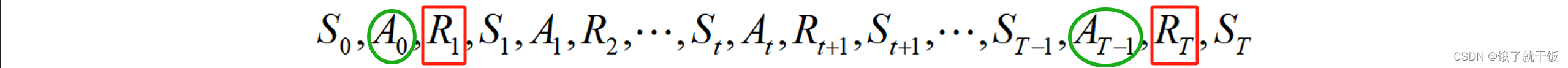
延時越長時RT，對Gt的影響越小： 延時越長時RT，即T越大，參數γ經過T指數后參數變得很小，因此對Gt的影響越小。
強化學習的目的或目標： 尋找到一個能夠使累積折扣獎勵Gt最大的最優策略。如果該策略可以使得每一個時刻的累積折扣獎勵都最大，這個策略是最優的。

有了累積折扣獎勵函數之后，進一步定義兩個值函數：狀態值函數、動作值函數。

上面的Rt+1應該寫成Rt+k

從上面的式子可以看出來，對于每個狀態和每一個動作都會對應一個動作值，對于離散的狀態空間和動作空間來講那么動作值的個數應該是有限的，此時將會使用一個表來表示這個Q，之后會學習一種基于表的強化學習方法。
‘狀態值函數和動作值函數之間是可以相互轉換的。’

上面是假設s的下一個狀態為s'
詳細解釋與推導：

動態規劃的核心：貝爾曼方程。下面的兩個方程認真一點都能寫出來，需要注意的是在
1）狀態值函數表達的貝爾曼方程中的r是在s狀態下執行動作a之后得到的獎勵r，在得到的這個方程的時候是這么簡寫的。
2）寫動作值函數的貝爾曼方程時第2個Q函數中的s和a都是下一時刻的狀態和下一時刻的動作。因此動作值函數表達的貝爾曼方程中有4個變量：當前時刻狀態s,當前時刻的動作a,下一時刻的狀態s',下一時刻的動作a'，比較復雜，而狀態值函數表達的貝爾曼方程中只有2個變量：當前狀態s和下一時刻狀態s'，形式較為簡單。因此實際中使用狀態值函數更多。
3）兩種貝爾曼方程中的r是基于三元函數的。即r=r(s,a,s')，之前我們還定義過R=R(s,a)，此處不是二元的。為什么是3元呢？：因為在方程里面求和的時候，求和符號下面的變量已知了，就代表下一時刻s’已經知道了，那r就采用三元的定義形式了。不過也可以寫成二元的獎勵函數，因此有了下面的基于二元獎勵函數的貝爾曼方程。
4）三元價值函數和二元值函數的關系




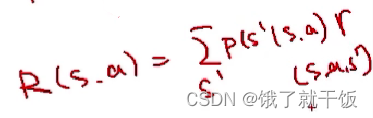
貝爾曼方程與動態規劃的關系：貝爾曼是動態規劃的發明人，s狀態下的狀態值函數可以使用下一時刻狀態s’的狀態值函數表示出來，也是動態規劃的原理。

2.3節 策略評估

智能體思考在當前環境下要做出什么動作的過程就叫策略。


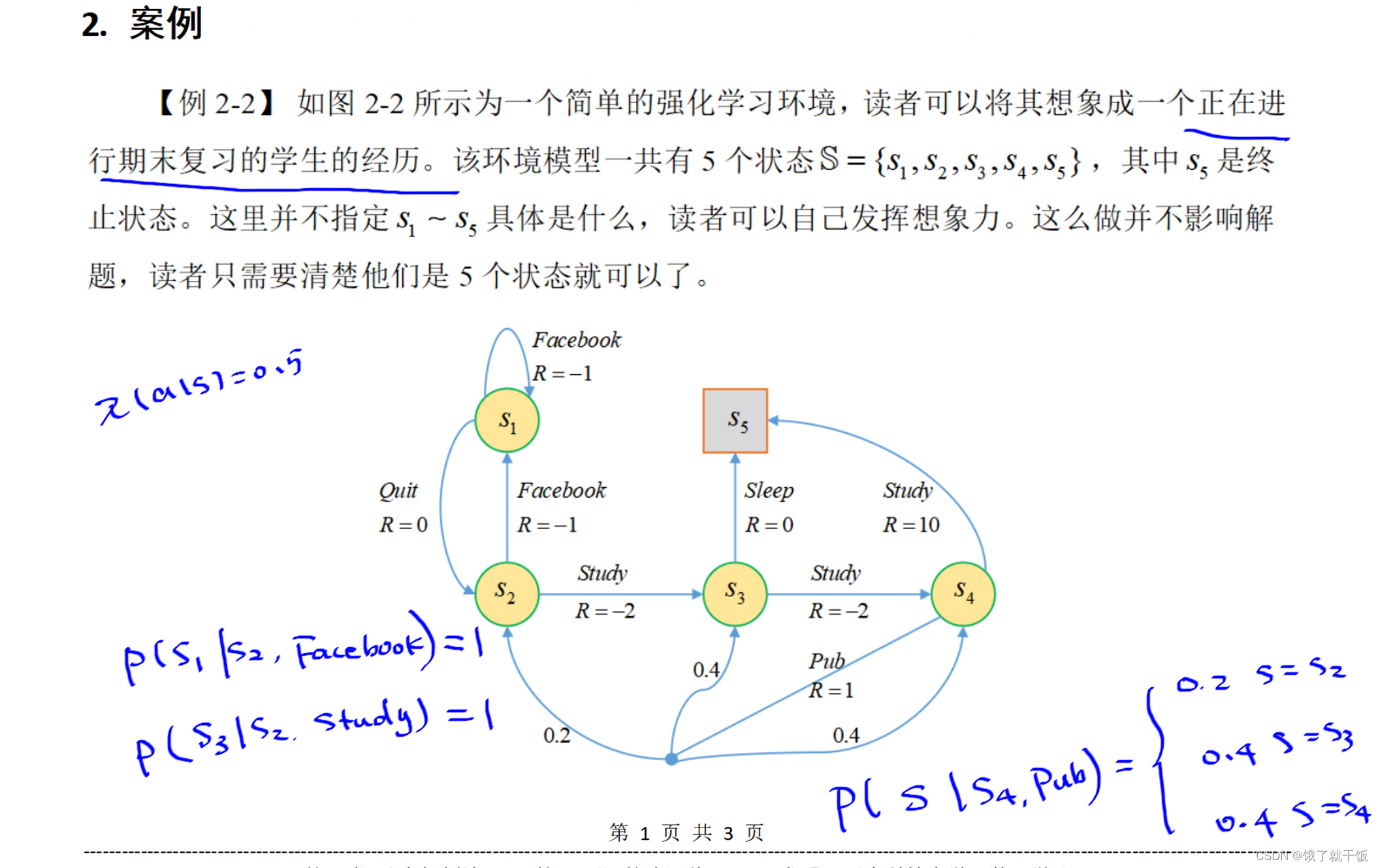
所有的終止狀態的狀態值函數都是0
下圖中的狀態轉移概率在上圖中已經展示了一部分，比較好寫。使用的策略是平均策略，也即時在不管在哪個狀態下，采取任意一個動作的概率均為0.5，也因為是每個狀態下可采取的動作只有兩個，定義策略時采用平均策略較好。

下圖中基于狀態值函數的貝爾曼方程中的4個方程就嚴格按照方程寫是比較好寫出來的。解出來的結果見下圖

在V4的時候稍微麻煩一點，部分計算如下圖

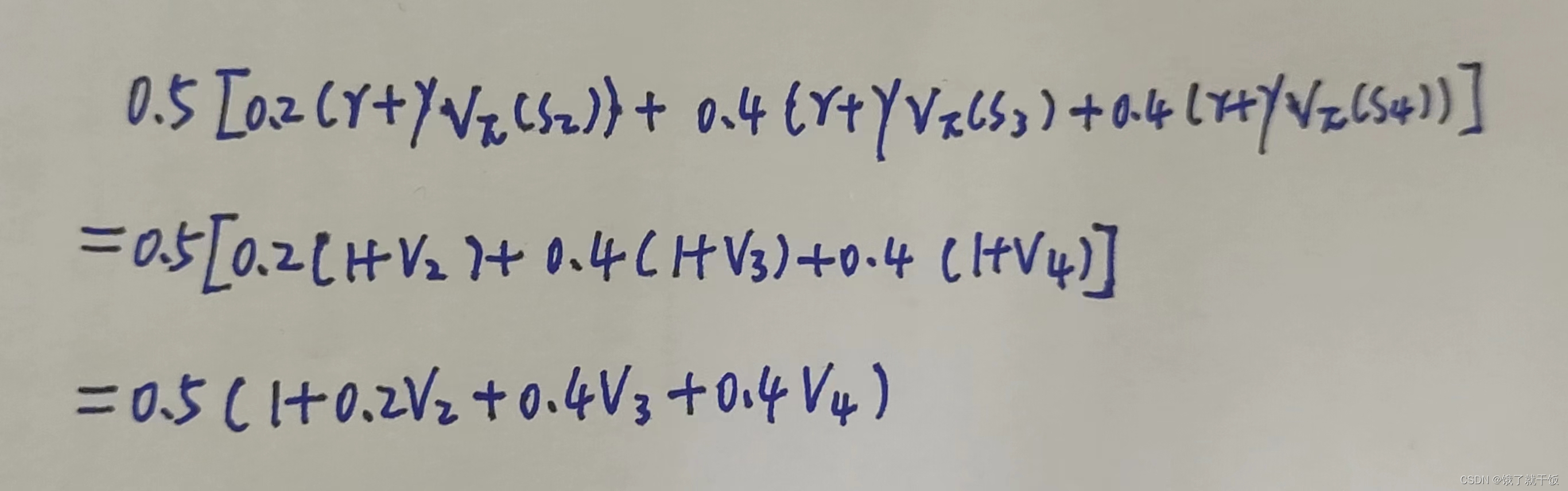
需要注意的一點：
聯立的這個4元方程組一定是有解的，原因是：顯然可以看出第1個方程中V2可以使用V1表示，第2個方程中V3可以使用V2表示，第3個方程中V4可以使用V3表示，而第4個方程中可以將所有變量均使用V1去表示，因此這個方程組可以合并成一個關于V1的方程，則必有解。我認為其他的場景下使用動態規劃模型建模的強化學習方法使用方程組法去解則其解也類似如此唯一。
如果在秩的角度來解釋：每個方程都是根據在不同狀態下寫出來的，每個狀態是獨立的，因此這幾個方程是獨立的，是不相關的，因此方程組的秩是滿秩的，因此有唯一解。
當方程組很大的時候采用高斯消元法已經不夠用了，此時使用迭代法來求解一個方程組。即先設置一個初值，經過貝爾曼方程的逐次計算得到一個迭代序列，經過多次迭代就會得到一個最終的近似解。迭代法之后用的更多，優點是速度快、方法簡單，缺點是得到的解是近似解，不是精確解。

假如有一個新的策略π’，根據這個策略算出來一系列的狀態值，這些狀態值都要大于原來的策略π算出來的狀態值，那么這個新策略π’就要比原來的策略π要好。具體為什么是這樣，暫時不太清楚，存疑后解。

2.4節 策略改進

根據下面的定義可以得出結論：找最優的策略的就是去找最大的狀態值函數。

π’(s)表示根據π’策略從狀態s開始下一步執行的動作
策略改進定理：

證明：

上面證明的一個說明：在V的時候，下標是π或π’似乎無關緊要，不用糾結，當然認真摳細節的話，我覺著應該是薛定諤的V。

說明：策略改進定理是策略得到改進的充分條件

滿足（2-14）的最簡單的策略就是貪婪策略
簡單解釋為：選擇在狀態s時使得動作值函數最大的動作作為策略。
貪心策略一定是策略改進定理中的（2-14）式的。紅色的公式是用動作值函數來表示狀態值函數的公式。從該公式中可以看出，狀態值函數是動作值函數的期望值，而π’(s)如果是選擇在狀態s時使得動作值函數最大的動作，那么Qπ(s,π’(s))則是最大的動作值函數，必大于等于動作值函數的期望值，也即是必大于等于狀態值函數，因此滿足（2-14）式，故該策略可有效改進。

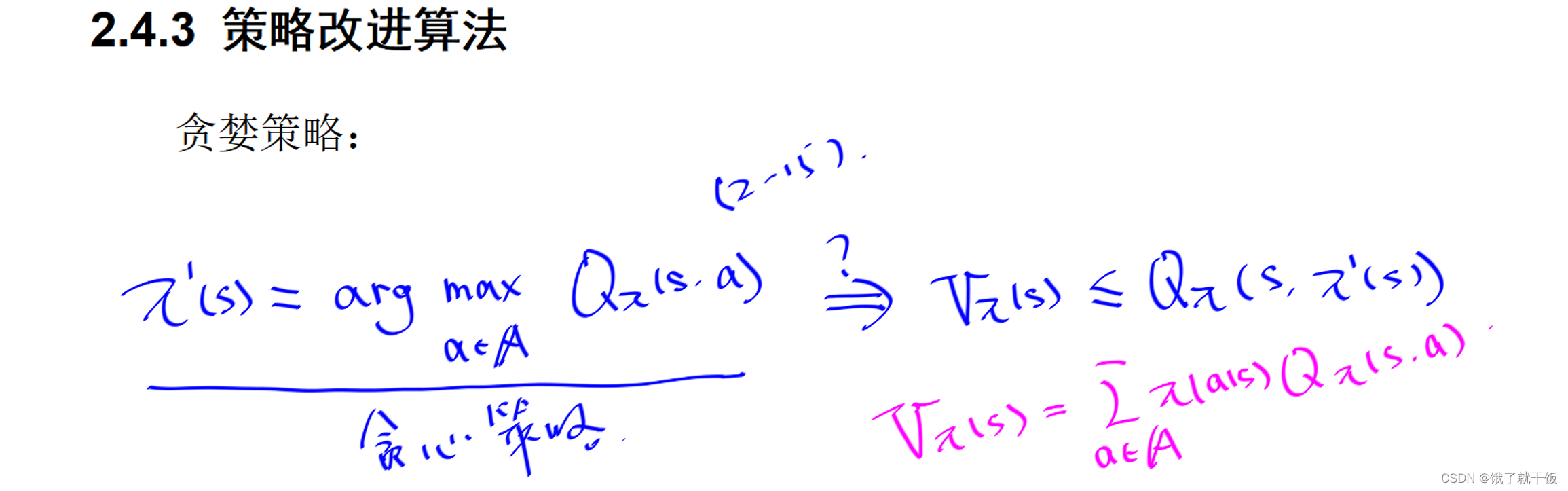
由下圖Qπ(s,a)的表達公式，如果已知Vπ(s’)要去計算Qπ(s,a)需要知道狀態轉移函數p(s’|s,a)，如果不知道狀態轉移函數p(s’|s,a)怎么辦？可以使用基于動作值函數的貝爾曼方程去求解

基于動作值的貝爾曼方程見下圖：（具體如何根據下圖求解狀態轉移概率有待研究）


下面示例中的被劃掉的0其實不應該寫的。

2.5節 最優值函數與最優策略

2.6節 值迭代與策略迭代

2.7節 動態規劃求解最優策略