快速排序的基本思想

快速排序是Hoare于1962年提出的一種二叉樹結構的交換排序方法

其基本思想為：

任取待排序元素序列中的某元素作為基準值，按照該排序碼將待排序集合分割成兩子序列，左子序列中所有元素均小于基準值，右序列中所有元素均大于基準值，然后最左右子序列重復該過程，直到所有元素都排列在相應位置上為止

// 假設按照升序對array數組中[left, right)區間中的元素進行排序
void QuickSort(int array[], int left, int right)
{if(right - left <= 1)return;// 按照基準值對array數組的 [left, right)區間中的元素進行劃分int div = partion(array, left, right);// 劃分成功后以div為邊界形成了左右兩部分 [left, div) 和 [div+1, right)// 遞歸排[left, div)QuickSort(array, left, div);// 遞歸排[div+1, right)QuickSort(array, div+1, right);
}

上述為快速排序遞歸實現的主框架，發現與二叉樹前序遍歷規則非常像，同學們在寫遞歸框架時可想想二叉樹前序遍歷規則即可快速寫出來，后序只需分析如何按照基準值來對區間中數據進行劃分的方式即可。

劃分區間的常見方式

將區間按照基準值劃分為左右兩半部分的常見方式有三種，

1. hoare方法
2. 挖坑法
3. 前后指針法?

三種方法是排key左右區間的不同，整體快排的思想是遞歸?

1.hoare方法

https://img-blog.csdnimg.cn/07ddcfdc56874b2a9d12f585534ac87e.gif#pic_center

1.1圖示

定義left和right來找大和找小

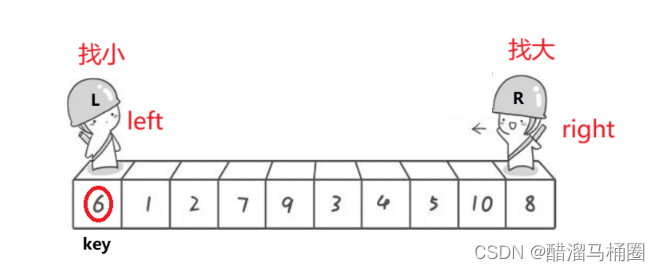
right先走找大，left再走找小，找到交換

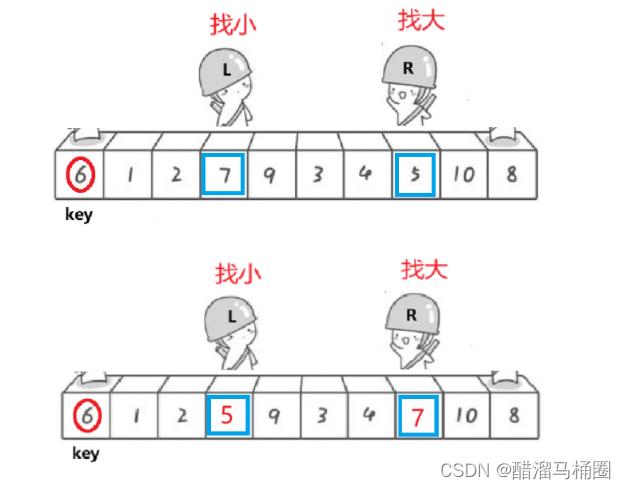
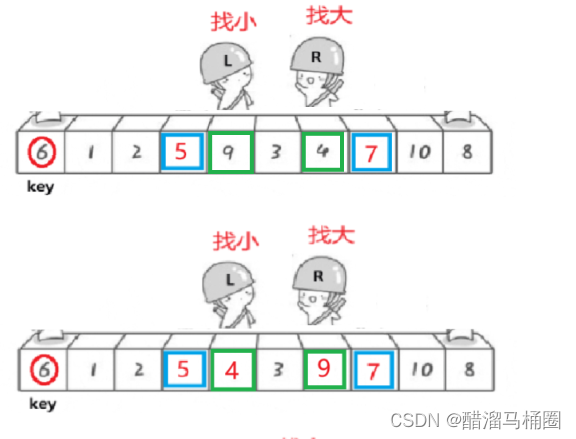
繼續找大找小

相遇停下來，和key交換

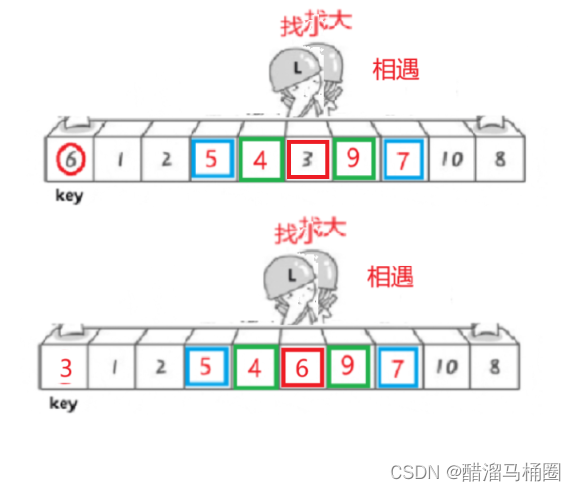
1.2為什么相遇位置一定比key小

這里我們有一個問題：為什么相遇位置一定比key小？

因為右邊先走

相遇有兩種情況：

1. right遇left -> left先走，right沒有遇到比key小的，一直走，直到遇到left停下來，left存的是比key小的值
2. left遇right?-> right先走，left沒有遇到比key大的，一直走，直到遇到right停下來，right存的是比key大的值
3. 所以我們得出一個結論，左邊做key，右邊先走；右邊做key，左邊先走

如果左邊有序，右邊也有序，整體就有序了

那么如何讓左右有序呢？

類似二叉樹，遞歸左樹和右樹

第一遍排序后的left和right的范圍是：[begin,keyi-1]，keyi，[keyi+1,end]

然后繼續遞歸，直到這個區間只有一個值或者不存在

1.3代碼示例

//hoare方法
int PartSort1(int*a,int begin,int end)
{int midi = GetMidi(a, begin, end);Swap(&a[midi], &a[begin]);int left = begin, right = end;int keyi = begin;while (left < right){//右邊找小while (left < right && a[right] >= a[keyi]){--right;}//左邊找大while (left < right && a[left] <= a[keyi]){++left;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);keyi = left;return keyi;
}

2.挖坑法?

https://img-blog.csdnimg.cn/c2dde0e21f32461fb43db524559ca36d.gif#pic_center

2.1圖示

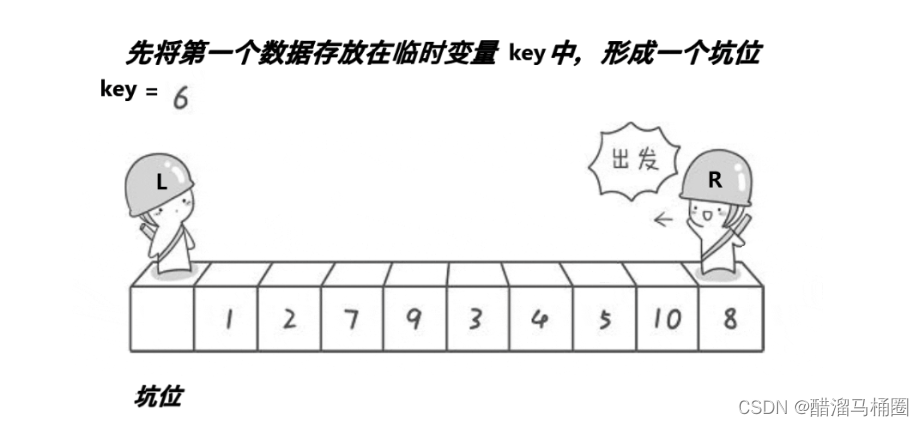
right找小，left找大，right先走，找到小和坑位交換，然后left走，left找到大之后和坑位交換，交替進行直到相遇

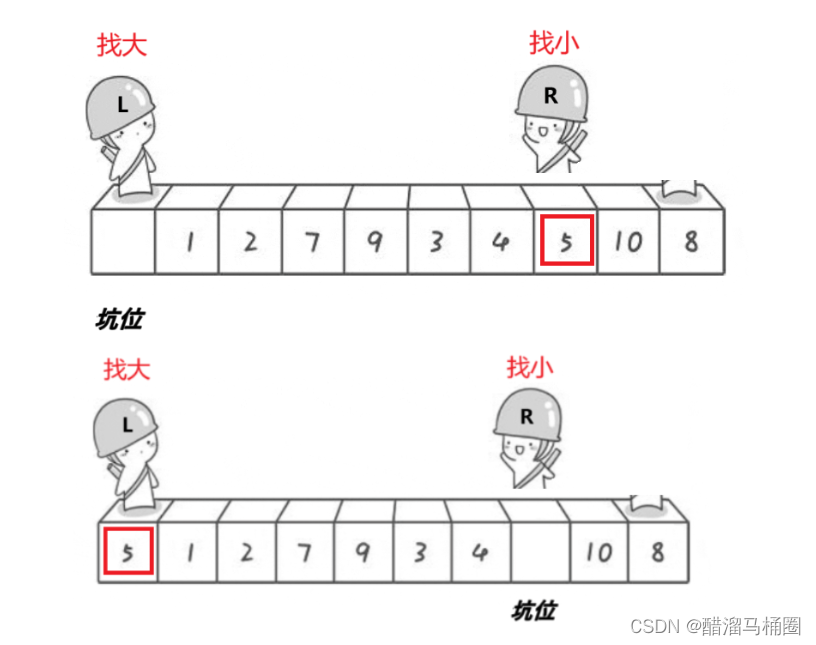
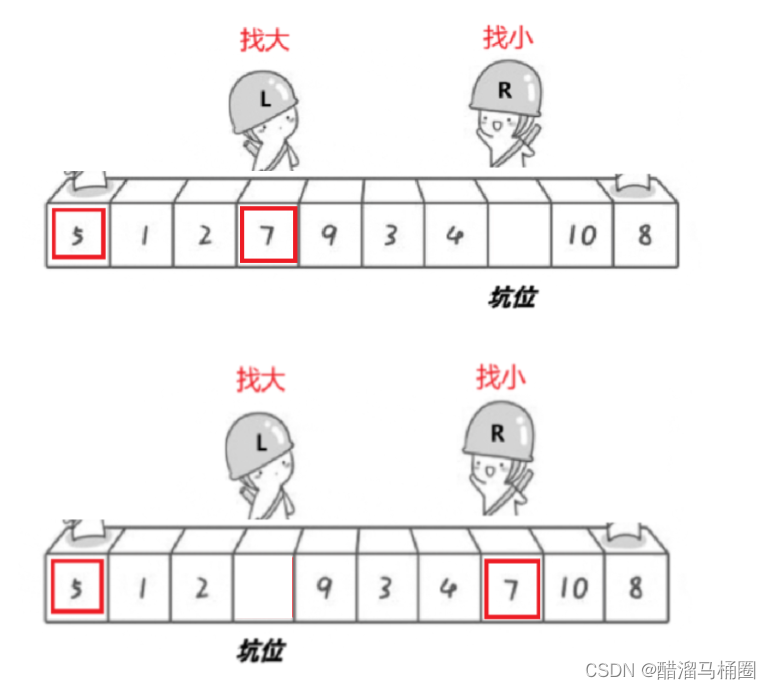
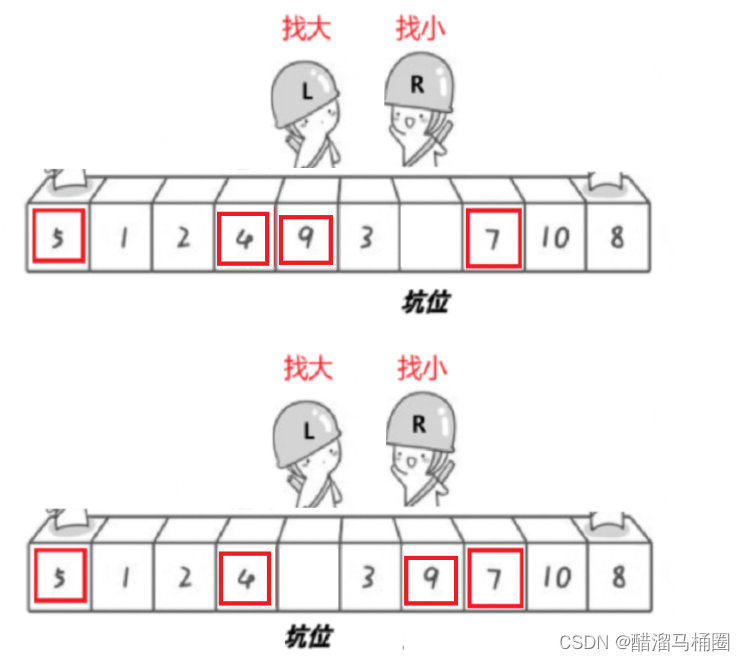
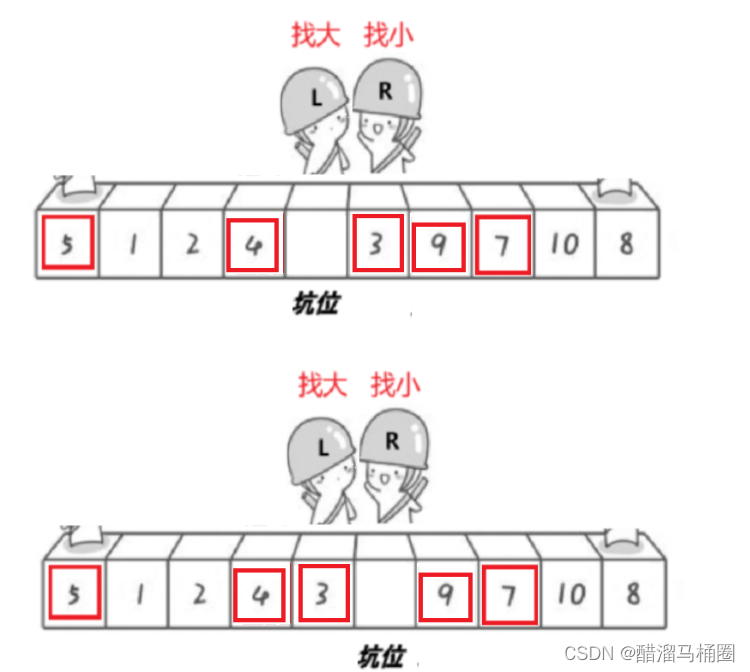
他們一定會相遇到坑的位置

相遇之后將key的值放到坑位中，這時候key左邊就是比key小的，key右邊就是比key大的

2.2代碼示例

我們寫一個挖坑法的函數來排keyi左右的數據

先用三數取中方法得到keyi，定義一個key保存keyi的值，定義一個坑位holei先放到begin

• 右邊找小，填到左邊的坑里，右邊成為新的坑
• 左邊找大，填到右邊的坑里，左邊成為新的坑?
• 相遇后將key放到坑里，返回坑的下標?

//挖坑法
int PartSort2(int* a, int begin, int end)
{int midi = GetMidi(a, begin, end);Swap(&a[midi], &a[begin]);int key = a[begin];int holei = begin;while (begin < end){//右邊找小while (begin < end && a[end] <= key)--end;a[holei] = a[end];holei = end;//左邊找大while (begin < end && a[begin] >= key)++begin;a[holei] = a[begin];holei = begin;}//相遇a[holei] = key;return holei;
}

3.前后指針法

https://img-blog.csdnimg.cn/8baec430614e47dfa382926553830c14.gif#pic_center

3.1圖示

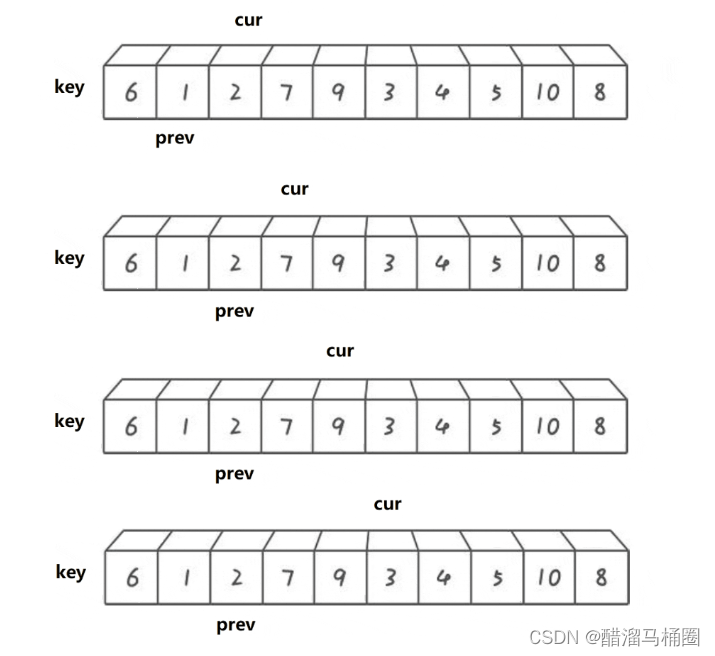
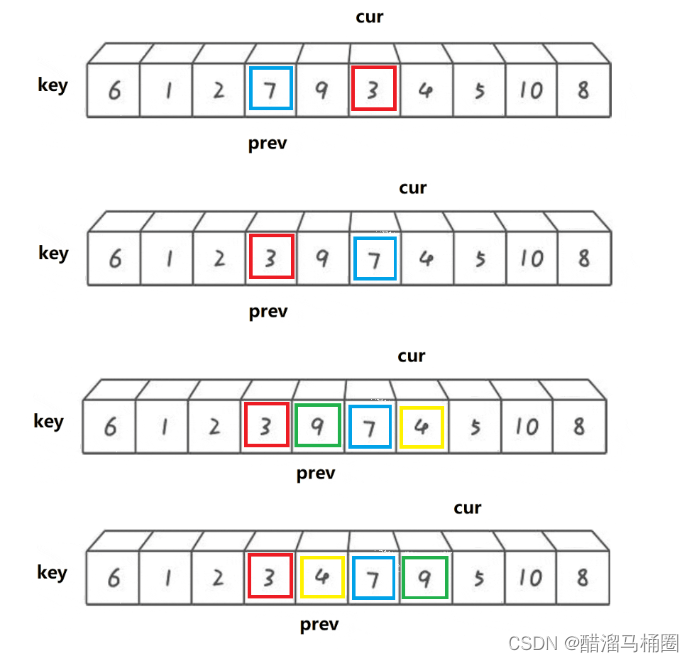
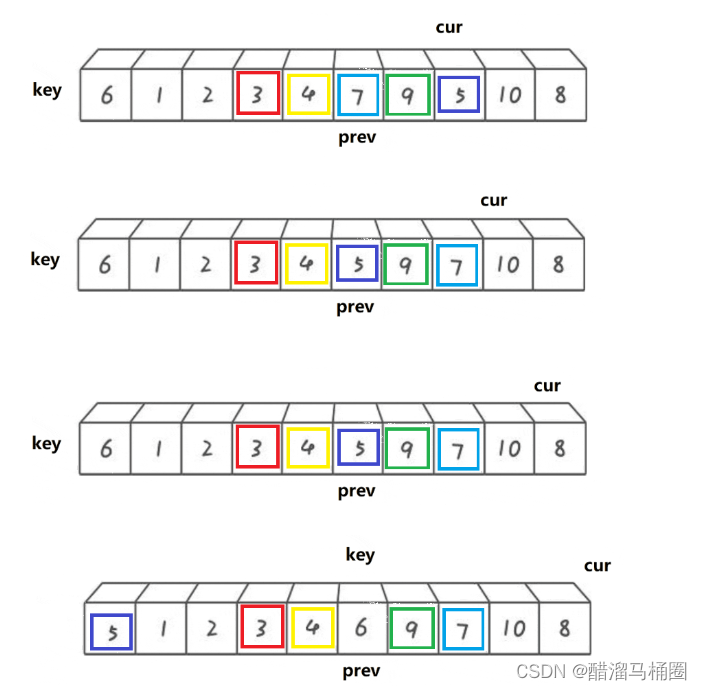
prev要不就是緊跟cur，要不prev和cur之間就是比key大的值

3.2代碼示例

//前后指針法
int PartSort3(int* a, int begin, int end)
{int midi = GetMidi(a, begin, end);Swap(&a[midi], &a[begin]);int keyi = begin;int prev = begin, cur = begin + 1;while (cur <= end){//if (a[cur] < a[keyi])//{//	++prev;//	Swap(&a[prev], &a[cur]);//	++cur;//}//else//	++cur;if (a[cur] < a[keyi] && ++prev != cur)Swap(&a[prev], &a[cur]);++cur;}Swap(&a[keyi], &a[prev]);keyi = prev;return keyi;
}

4.快速排序優化

1. 三數取中法選key
2. 遞歸到小的子區間時，可以考慮使用插入排序

4.1三數取中方法

這里我們的key默認取的是第一個數，但是這種情況有個弊端，不能保證key一定是那個中間值，可能是最小的，也可能是最大的

但是理想情況下，key選中間值是效率最高的，每次都是二分?

這里就有一個方法能很好的解決這個問題：三數取中

我們寫一個取中函數，將中間值與begin交換，還是將key給到begin

int GetMidi(int* a, int begin, int end)
{int midi = (begin + end) / 2;if (a[begin] < a[midi]){if (a[midi] < a[end])return midi;else if (a[begin] > a[end])return begin;elsereturn end;}else{if (a[midi] > a[end])return midi;else if (a[end] > a[begin])return begin;elsereturn end;}
}

三數取中可以排除掉最壞的情況，相對而言可以提高效率

4.2小區間優化

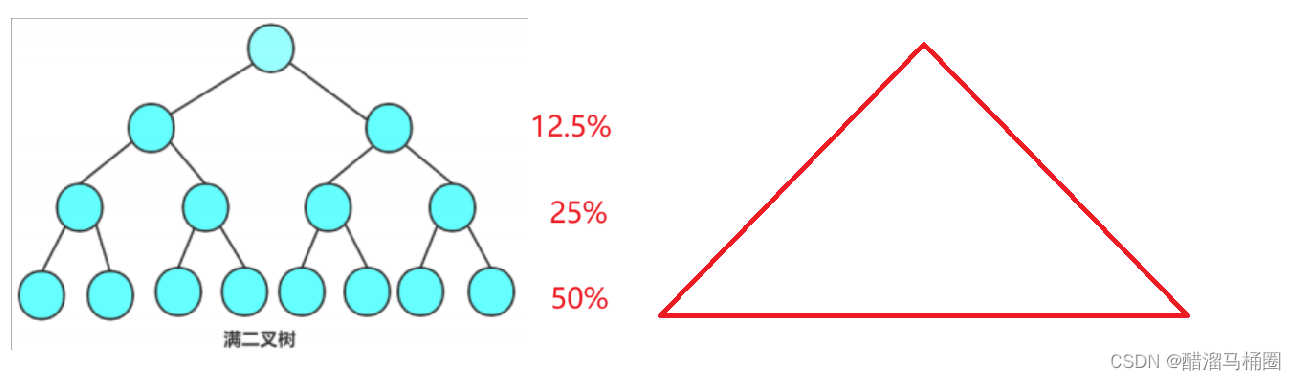
如果是滿二叉樹，最后一層占50%的節點，倒數第二層占25%，倒數第三層占12.5%

假設我們要對這五個數排序，就需要調用六次遞歸，這代價是非常大的

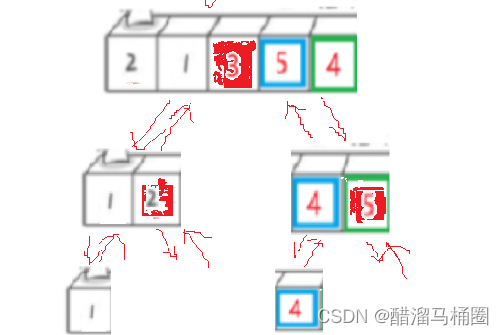
我們可以使用插入排序，插入排序對局部的適應性是很好的，所以我們在這個區間縮小的一定范圍的時候就可以使用插入排序

一般選擇最后三到四層，因為最后三層就占據了將就90%的遞歸，將最后三層的遞歸消除是能夠明顯提高效率的

剩下的區間不一定是從0開始的，也有可能是后半段，所以這里插入排序從begin開始

總代碼

#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <stdlib.h>
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
void InsertSort(int* a, int n)
{for (int i = 0; i < n - 1; i++){int end = i;int tmp = a[end + 1];while (end >= 0){if (tmp < a[end]){a[end + 1] = a[end];end--;}elsebreak;}a[end + 1] = tmp;}
}
int GetMidi(int* a, int begin, int end)
{int midi = (begin + end) / 2;if (a[begin] < a[midi]){if (a[midi] < a[end])return midi;else if (a[begin] > a[end])return begin;elsereturn end;}else{if (a[midi] > a[end])return midi;else if (a[end] > a[begin])return begin;elsereturn end;}
}
//hoare方法
int PartSort1(int*a,int begin,int end)
{int midi = GetMidi(a, begin, end);Swap(&a[midi], &a[begin]);int left = begin, right = end;int keyi = begin;while (left < right){//右邊找小while (left < right && a[right] >= a[keyi]){--right;}//左邊找大while (left < right && a[left] <= a[keyi]){++left;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);keyi = left;return keyi;
}
//挖坑法
int PartSort2(int* a, int begin, int end)
{int midi = GetMidi(a, begin, end);Swap(&a[midi], &a[begin]);int key = a[begin];int holei = begin;while (begin < end){//右邊找小while (begin < end && a[end] <= key)--end;a[holei] = a[end];holei = end;//左邊找大while (begin < end && a[begin] >= key)++begin;a[holei] = a[begin];holei = begin;}//相遇a[holei] = key;return holei;
}
//前后指針法
int PartSort3(int* a, int begin, int end)
{int midi = GetMidi(a, begin, end);Swap(&a[midi], &a[begin]);int keyi = begin;int prev = begin, cur = begin + 1;while (cur <= end){//if (a[cur] < a[keyi])//{//	++prev;//	Swap(&a[prev], &a[cur]);//	++cur;//}//else//	++cur;if (a[cur] < a[keyi] && ++prev != cur)Swap(&a[prev], &a[cur]);++cur;}Swap(&a[keyi], &a[prev]);keyi = prev;return keyi;
}
//快排
void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;if (end - begin + 1 <= 10)InsertSort(a + begin, end - begin + 1);else{//hoare法//int keyi = PratSort1(a, begin, end);//int keyi = PartSort2(a, begin, end);int keyi = PartSort3(a, begin, end);QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);}
}
int main()
{int a[] = { 9,8,7,6,6,5,4,3,2,1,10,14,12,11,15 };int n = sizeof(a) / sizeof(a[0]);QuickSort(a, 0, n - 1);for (int i = 0; i < n; i++){printf("%d ", a[i]);}return 0;
}