說在前面

🎈不知道大家對于算法的學習是一個怎樣的心態呢？為了面試還是因為興趣？不管是處于什么原因，算法學習需要持續保持，今天讓我們一起來看看這一道題目————圖中的最長環，圖論題目中比較常見的環路問題。

題目描述

給你一個 n?個節點的 有向圖?，節點編號為?0?到?n - 1?，其中每個節點?至多?有一條出邊。

圖用一個大小為 n?下標從?0?開始的數組?edges?表示，節點 i?到節點?edges[i]?之間有一條有向邊。如果節點?i?沒有出邊，那么?edges[i] == -1?。

請你返回圖中的 最長?環，如果沒有任何環，請返回 -1?。

一個環指的是起點和終點是 同一個?節點的路徑。

示例 1：

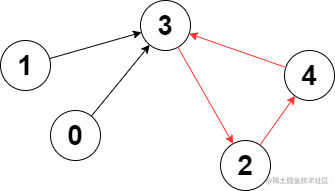
輸入：edges = [3,3,4,2,3]
輸出去：3
解釋：圖中的最長環是：2 -> 4 -> 3 -> 2 。
這個環的長度為 3 ，所以返回 3 。

示例 2：

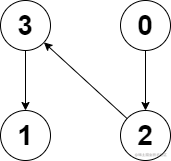
輸入：edges = [2,-1,3,1]
輸出：-1
解釋：圖中沒有任何環。

提示：

n == edges.length
2 <= n <= 10^5
-1 <= edges[i] < n
edges[i] != i

思路分析

題目的要求很清晰，就是要我們找出單向連通圖中的最長環，那么在一個圖中我們要怎樣來判斷有沒有存在環呢？因為這道題目中的圖是單向圖，所以我們可以很簡單找出圖中的環，如下圖：

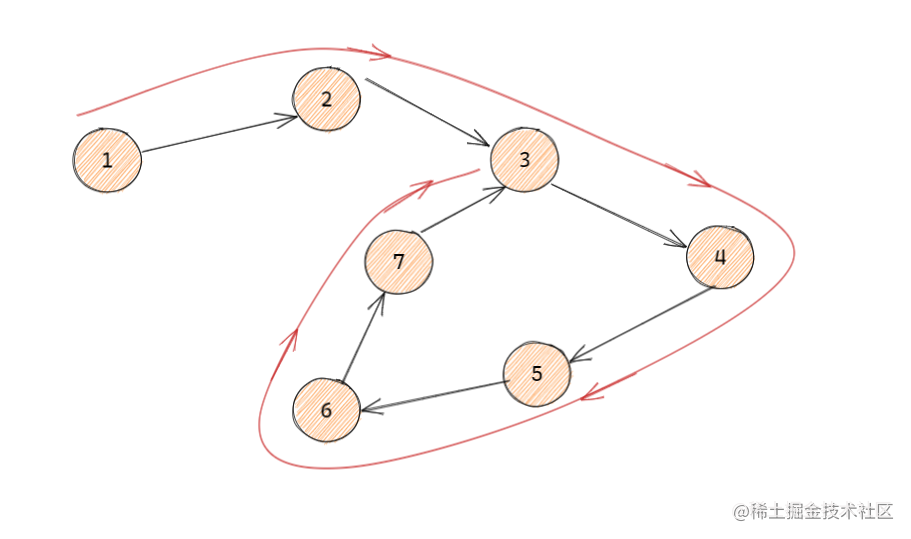
我們從節點1出發，遍歷過的節點都做上標記，然后不斷的往圖的下一個節點遍歷，直到遇到已經做過標記的節點，則說明其前面也遍歷過，也即是已經形成了環。這樣說的話我們是不是可以把所有節點都當成起點走一遍，找出所有環中的最長環就可以？讓我們動手寫代碼試一下，按照這個思路我們可以寫出這樣一段代碼：

/*** @param {number[]} edges* @return {number}*/var longestCycle = function(edges) {let res = -1;const dfs = (node,steps,step = 0)=>{if(edges[node] == -1) return -1;if(steps[node] <= step){res = Math.max(step - steps[node],res);return step;}steps[node] = step;dfs(edges[node],steps,step + 1);}for(let i = 0; i < edges.length; i++){dfs(i,new Array(edges.length).fill(Infinity));}return res > 0 ? res : -1;
};

測試一下，好像沒問題，然后自信提交代碼

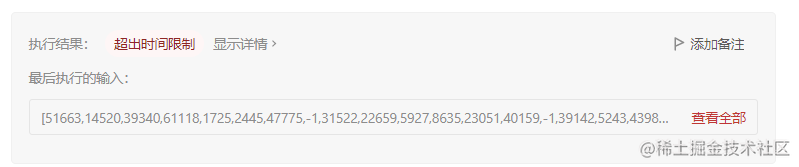
回頭看一下數據規模2 <= n <= 10^5,這樣做確實太暴力了，那就來看看可以怎么優化：

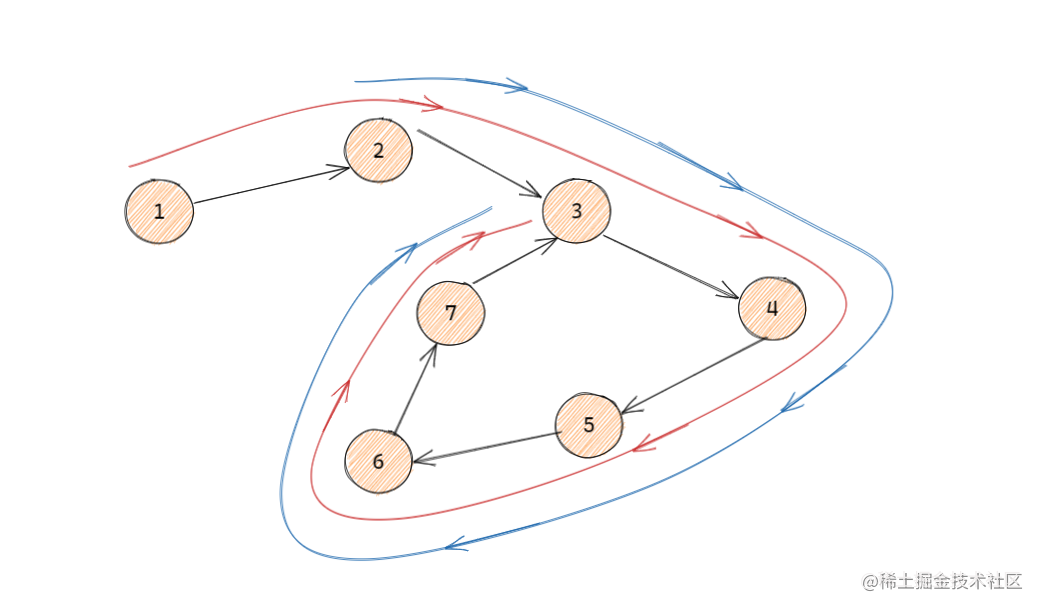
上圖中橙色路徑為從節點1出發的遍歷路線，藍色路徑為從節點2出發的遍歷路線，從圖中我們可以很明顯的看成藍色路線是橙色路線中的一部分，因為節點2在節點1的遍歷路徑中，所以節點2往后的遍歷路線一定是包含在節點1的遍歷路線中，所以我們可以記錄一下每個節點的遍歷情況，如果是已經遍歷過的節點的話，我們不應該重復遍歷，所以代碼可以這樣進行優化：

• 使用一個數組來記錄遍歷過程中每一個節點的遍歷情況(visited)
• 使用一個map來存放在當前路徑中已經遍歷過的節點所需步數(steps)
• 遇到map中存在的節點時更新最長環長度

AC代碼

/*** @param {number[]} edges* @return {number}*/var longestCycle = function(edges) {let res = -1;const dfs = (node,steps = {},step = 0)=>{if(visited[node] || steps[node] <= step || edges[node] == -1){if(steps[node] < step) res = Math.max(step - steps[node],res);return;}steps[node] = step; visited[node] = true;dfs(edges[node],steps,step + 1);}const visited = new Array(edges.length).fill(false);for(let i = 0; i < edges.length; i++) dfs(i);return res;
};

公眾號

關注公眾號『前端也能這么有趣』，獲取更多有趣內容。

說在后面

🎉 這里是 JYeontu，現在是一名前端工程師，有空會刷刷算法題，平時喜歡打羽毛球 🏸 ，平時也喜歡寫些東西，既為自己記錄 📋，也希望可以對大家有那么一丟丟的幫助，寫的不好望多多諒解 🙇，寫錯的地方望指出，定會認真改進 😊，偶爾也會在自己的公眾號『前端也能這么有趣』發一些比較有趣的文章，有興趣的也可以關注下。在此謝謝大家的支持，我們下文再見 🙌。