1. 概述

	方法	適用問題	模型特點	模型類型	學習策略	損失函數	學習算法
1	感知機	二分類	分離超平面	判別模型	極小化誤分點到超平面距離	誤分點到超平面距離	SGD
2	KNN	多分類，回歸	特征空間，樣本點	判別模型	-	-	-
3	樸素貝葉斯	多分類	特征與類別的聯合概率分布，條件獨立假設	生成模型	極大似然估計，極大后驗概率估計	對數似然損失	概率計算公式，EM算法
4	DT	多分類，回歸	分類樹，回歸樹	判別模型	正則化的極大似然估計	對數似然損失	特征選擇，生成，剪枝
5	LR與最大熵模型	多分類	特征條件下類別的條件概率分布，對數線性模型	判別模型	極大似然估計，正則化的極大似然估計	邏輯斯蒂損失	改進的迭代尺度算法，梯度下降，擬牛頓法
6	SVM	二分類	分離超平面，核技巧	判別模型	極小化正則化合頁損失，軟間隔最大化	合頁損失	序列最小最優算法SMO
7	提升方法	二分類	弱分類器的線性組合	判別模型	極小化加法模型的指數損失	指數損失	前向分布加法
8	EM算法	概率模型參數估計	含隱變量概率模型	-	極大似然估計，極大后驗概率估計	對數似然損失	迭代算法
9	隱馬爾可夫模型	標注	觀測序列與狀態序列的聯合概率分布模型	生成模型	極大似然估計，極大后驗概率估計	對數似然損失	概率計算公式，EM算法
10	條件隨機場	標注	狀態序列條件下觀測序列的條件概率分布，對數線性模型	判別模型	極大似然估計，正則化極大似然估計	對數似然損失	改進的迭代尺度算法，GD，擬牛頓法

2. 適用問題

1. 分類問題是從實例的特征向量到類標記的預測問題；
2. 標注問題是從觀測序列到標記序列(或狀態序列)的預測問題，可以認為分類問題是標注問題的特殊情況；

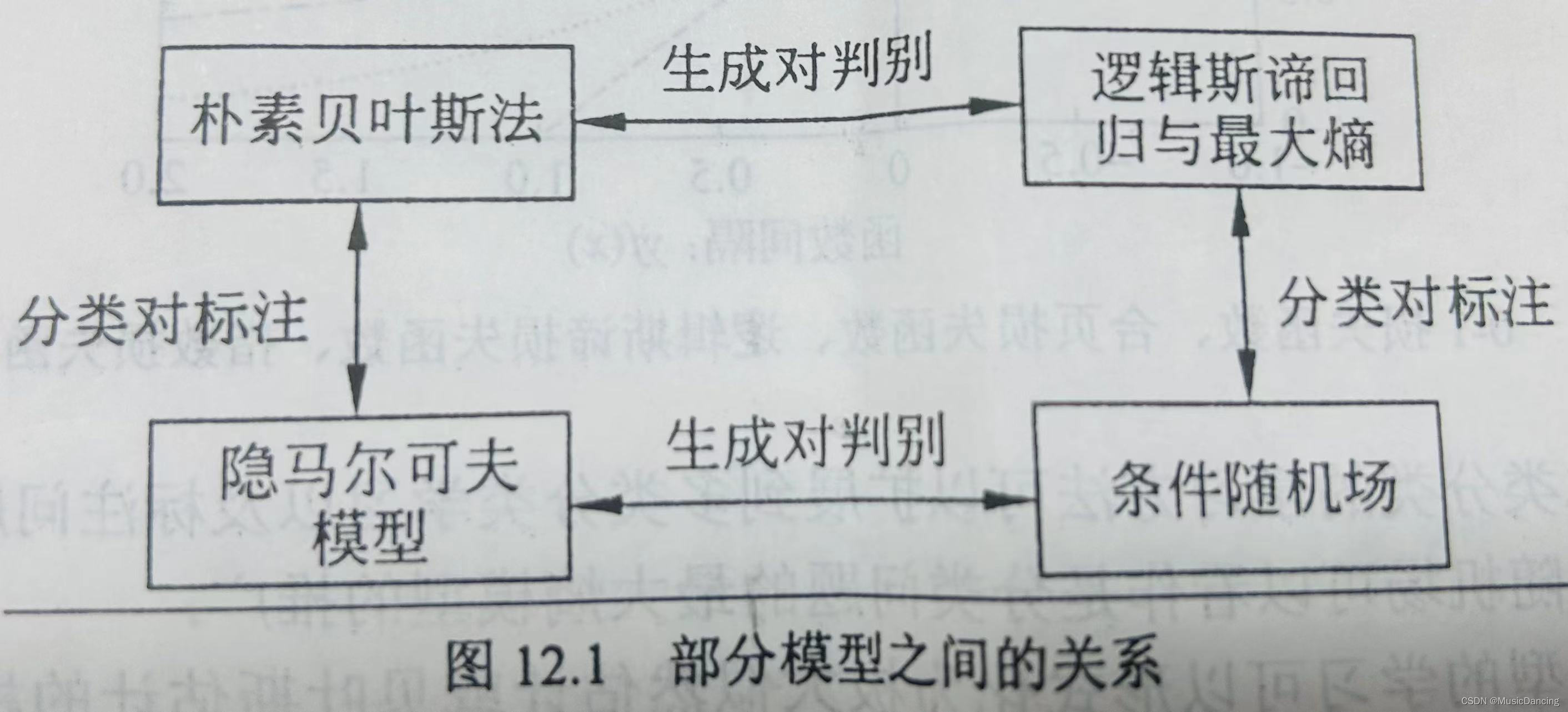
??????? 分類問題與標注問題都可以寫成條件概率分布P(Y|X)或決策函數Y=f(X)的形式，前者表示給定輸入條件下輸出的概率模型，后者表示輸入到輸出的非概率模型。有時模型更直接地表示為概率模型(如樸素貝葉斯、隱馬爾可夫)，或非概率模型(如感知機，knn，SVM，提升方法)，有時模型兼有兩種解釋(如DT，LR與最大熵模型，條件隨機場)。

3. 模型

??????? 直接學習條件概率分布P(Y|X)或決策函數Y=f(X)的方法為判別方法，對應的模型是判別模型，如感知機，knn，DT，LR與最大熵模型，SVM，提升方法，條件隨機場。

??????? 首先學習聯合概率分布P(Y|X)，從而求得條件概率分布P(Y|X)的方法是生成方法，對應的
模型是生成模型，如樸素貝葉斯、隱馬爾可夫。可以用非監督學習的方法學習生成模型，樸素貝葉斯、隱馬爾可夫可應用EM算法學習。

DT是定義在一般的特征空間上的，可以含有連續變量或離散變量；
感知機、svm、knn的特征空間是歐氏空間。

??????? 感知機模型是線性模型，而LR與最大熵模型、條件隨機場是對數線性模型； knn、DT、SVM(包含核函數)、提升方法使用的是非線性模型。

???????

4. 學習策略

??????? 概率模型的學習可以形式化為極大似然估計或貝葉斯估計的極大后驗概率估計。這時，學習的策略是極小化對數似然損失或極小化正則化的對數似然損失 -logP(y|x) 。極大后驗概率估計時，正則化項是先驗概率的負對數。

???????? 統計學習的問題有了具體的形式后，就變成了最優化問題，最優化問題大多數時候沒有解析解，需要用數值計算的方法或啟發式的方法求解。SVM、LR與最大熵模型、條件隨機場是凸優化問題，存在全局最優解；而其他學習問題則不是凸優化問題，不能保證全局最優解存在。