Python房價分析（二）隨機森林分類模型

1 數據預處理

1.1 房價數據介紹

1.2 數據預處理

1.2.1?缺失值處理

1.2.2異常值處理

1.2.3 數據歸一化

1.2.4 分類特征編碼

2 隨機森林模型

2.1?模型概述

2.2 建模步驟

2.3 參數搜索過程

3模型評估

3.1 模型評估結果

3.2 混淆矩陣

3.3 繪制房價類別三分類的ROC曲線和AUC數值

3.4 特征重要性可視化

總結

往期精彩內容：

房價分析（0）反爬蟲機制_python爬取房價數據-CSDN博客

Python房價分析（一）pyton爬蟲-CSDN博客

Python房價分析（三）支持向量機SVM分類模型-CSDN博客

1 數據預處理

1.1 房價數據介紹

房價數據來源于上期Python爬蟲所獲取的數據

Python房價分析（一）pyton爬蟲-CSDN博客

本文采用宜昌市二手房數據進行講解，數據如圖所示，共3000條樣本，有區域、街道、房型、朝向、面積、樓層數、裝修類型、房屋結構、收藏數、價格 10個特征。

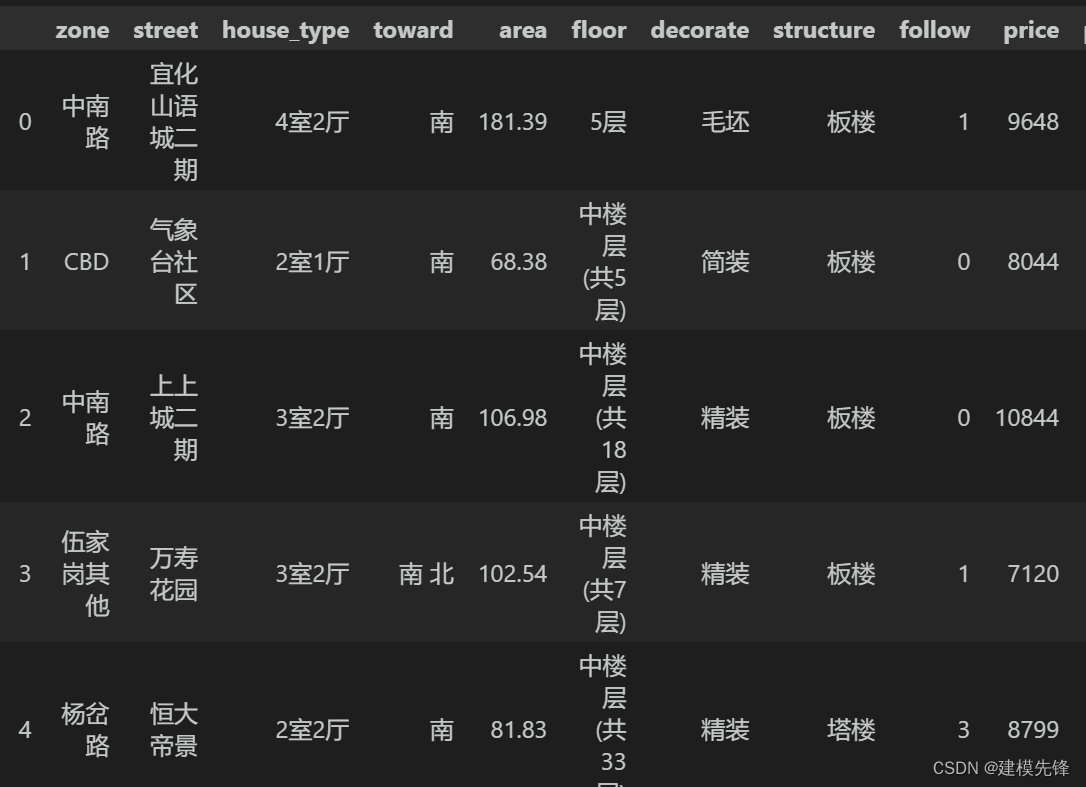
1.2 數據預處理

數據的偏離程度以及數據之間的關聯性會拉大整體數據標準差、造成統計偏見以及使數據帶有指向性偏好，這都會影響到我們最終模型和分析的結果，造成偏差，可見在進行統計與計算前對數據處理的必要性與重要性。

1.2.1?缺失值處理

????????對于給定的二手房數據中，可能某些特征存在一定的缺失值，當個別樣本缺失某些指標數據，模型的訓練就難以進行，若不對其進行缺失值填補則做分析時會被剔除進而不能參與最終的各項排名和綜合評價，影響后續的數據分析。

????????因此，基于本數據相關特征指標的缺失數量占總數據的比重較小，為了不丟棄大量隱藏在刪除對象中的信息，避免數據發生偏離，我們對數值型指標的缺失值進行0值填充，對于分類特征的缺失值，將“nan”（缺失值）視為有效的特征值，并為其創建指示符特征。

其中可選的插補策略包括

平均值mean
中位數median
眾數most_frequency
固定值constant

1.2.2異常值處理

對于異常值，不是刪除“異常數據”，而是將這些數據“拉回”到正常的值，本文通過確定指標的上下限，然后對于超過或者低于限值的數據均為限值，其上下限數值通過MAD（mean absolute deviation）即絕對值差中位數法判斷，來處理因子數據集中的異常值。

#對大于97.5%分位數的因子值，或小于2.5%分位數的因子值進行調整  容易理解，去除兩頭，只需調節參數，量化中較常用
def extreme_percentile(series,min=0.025,max=0.975):p = series.quantile([min,max])                  # 得到上下限的值return series.clip(p.iloc[0],p.iloc[1])  # 超出上下限的值，賦值為上下限

1.2.3 數據歸一化

由于數據集中大多數特征指標不滿足正態分布，不能采用常規的z-score 標準化。而數據集經過異常值處理后，減小了數據歸一化受離群點影響，我們采用Min-Max歸一化即極差法，將數據集中列數值縮放到0和1之間，來處理量綱的問題。

講解一下為什么需要歸一化

歸一化后加快了梯度下降求最優解的速度：如果機器學習模型使用梯度下降法求最優解時，歸一化往往非常有必要，否則很難收斂甚至不能收斂；
歸一化有可能提高精度：一些分類器需要計算樣本之間的距離（如歐氏距離），例如KNN。如果一個特征值域范圍非常大，那么距離計算就主要取決于這個特征，從而與實際情況相悖（比如這時實際情況是值域范圍小的特征更重要）

哪些機器學習算法不需要(需要)做歸一化?

概率模型（樹形模型）不需要歸一化，因為它們不關心變量的值，而是關心變量的分布和變量之間的條件概率，如決策樹、RF；
像Adaboost、SVM、LR、Knn、KMeans之類的最優化問題就需要歸一化。

1.2.4 分類特征編碼

對于數據集中的多分類特征變量，把不能量化的多分類變量量化，使得每個啞變量對模型的影響都細化，從而提高模型精準率。分類變量編碼能夠加速參數的更新速度；使得一個很大權值管理一個特征，拆分成了許多小的權值管理這個特征多個表示，降低了特征值擾動對模型的影響，模型具有更好的魯棒性。因此，我們采用OneHot獨熱編碼來為其創建分類類別特征。

from sklearn.preprocessing import OneHotEncoder
# 構造數據
X_train = [['male', 'from US', 'uses Safari'], ['female', 'from Europe', 'uses Firefox'], ['female', 'from China', 'uses Safari']]
# 編碼器
encoder = OneHotEncoder()
encoder = encoder.fit(X_train)
# 編碼
X = [['female', 'from Europe', 'uses Safari']]
X_transform = encoder.transform(X) 
X_transform.toarray()     # 默認返回的是稀疏矩陣, 用toarray()方法可以轉為np.array格式
>> array([[1., 0., 0., 1., 0., 0., 1.]])

2 隨機森林模型

2.1?模型概述

隨機森林是一種集成算法（Ensemble Learning），它是屬于Bagging類型。由于采用了集成算法，機器訓練后得到的結果會比那些只通過單個算法得到的結果更加準確，它可以用來解決分類和回歸問題[1]。隨機森林需要進行模擬和迭代，它通過隨機抽取樣本和特征，建立多棵相互不關聯的決策樹，每棵決策樹都能通過抽取的樣本和特征得出一個預測結果，通過綜合所有樹的結果取平均值，得到整個森林的回歸預測結果。具體算法結構如圖所示。

隨機森林有眾多優點，如：對特征很多的數據也可以適用 , 不用降維，不需要做特征選擇；可以輸出特征的重要性排序，方便邏輯解釋；可以判斷出不同特征之間的相互影響；訓練速度比較快；不容易過擬合；可以適用不平衡的數據等[2]。另外, 隨機森林不僅能處理離散型數據，還能處理連續型數據，而且不需要將數據集規范化。基于以上優點，選取隨機森林模型來對二手房價格進行分類與預測。

2.2 建模步驟

Step1.特征變量和目標變量提取，我們分析利用二手房價高、中、低三分類作為目標變量，把區域、街道、樓房名稱、戶型、朝向、建筑面積、樓層、裝修、結構、關注作為特征變量；

Step2.先對特征數據集進行標準化處理，然后進行訓練集和測試集數據劃分，本文將原始數據集進行分割，將訓練集與測試集進行劃分，將前70%的數據作為訓練集，后30%的數據作為測試集；

導入相關包

import pandas as pd
import numpy as np
from sklearn.ensemble import RandomForestClassifier  # 隨機森林分類
from sklearn.model_selection import train_test_split,GridSearchCV,cross_val_score
from sklearn.metrics import accuracy_score # 引入準確度評分函數
from sklearn.metrics import mean_squared_error
from sklearn.metrics import confusion_matrix, accuracy_score,classification_report
from sklearn import preprocessing
import warnings
warnings.filterwarnings('ignore')
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rc("font", family='Microsoft YaHei')

讀取預處理后的數據

# 讀取 預處理后的 數據
price_classify_data = pd.read_csv('yichang_deal.csv')
X = price_classify_data[['zone_label','street_label','type_label','toward_label','area','floor_label','decorate_label','structure_label','follow']]Y = price_classify_data['price_label']
# 標準化
X = preprocessing.scale(X)
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.3, random_state=200)  # 隨機數種子

Step3.利用Python的開源機器學習庫scikit-learn構建分類模型，采用隨機森林回歸方法進行建模，并通過設置不同決策樹數量來評估隨機森林方法的分類能力。

2.3 參數搜索過程

首先我們對最重要的超參數n_estimators即決策樹數量進行調試，通過不同數目的樹情況下，在訓練集和測試集上的均方根誤差來判斷

以及最優參數和最高得分進行分析，如下所示。

###調n_estimators參數
ScoreAll = []
for i in range(90,200,10):DT = RandomForestClassifier(n_estimators = i,random_state = 1) #,criterion = 'entropy'score = cross_val_score(DT,X_train,Y_train,cv=6).mean()ScoreAll.append([i,score])
ScoreAll = np.array(ScoreAll)max_score = np.where(ScoreAll==np.max(ScoreAll[:,1]))[0][0] ##這句話看似很長的，其實就是找出最高得分對應的索引
print("最優參數以及最高得分:",ScoreAll[max_score])  
plt.figure(figsize=[20,5])
plt.plot(ScoreAll[:,0],ScoreAll[:,1],'r-o',label='最高得分',color='orange')
plt.xlabel('n_estimators參數')
plt.ylabel('分數')
plt.grid()
plt.legend()
plt.show()

很明顯，決策樹個數設置在130的時候回歸森林預測模型的測試集均方根誤差最小，得分最高，效果最顯著。因此，我們通過網格搜索進行小范圍搜索，構建隨機森林預測模型時選取的決策樹個數為130。

在確定決策樹數量大概范圍后，搜索決策樹的最大深度的最高得分，如下所示。

# 探索max_depth的最佳參數
ScoreAll = []  
for i in range(10,30,3):  DT = RandomForestClassifier(n_estimators = 130,random_state = 1,max_depth =i ) #,criterion = 'entropy'  score = cross_val_score(DT,X_train,Y_train,cv=10).mean()  ScoreAll.append([i,score])  
ScoreAll = np.array(ScoreAll)  max_score = np.where(ScoreAll==np.max(ScoreAll[:,1]))[0][0] 
print("最優參數以及最高得分:",ScoreAll[max_score])    
plt.figure(figsize=[20,5])  
plt.plot(ScoreAll[:,0],ScoreAll[:,1]) 
plt.xlabel('max_depth最佳參數')
plt.ylabel('分數')
plt.grid()
plt.legend() 
plt.show()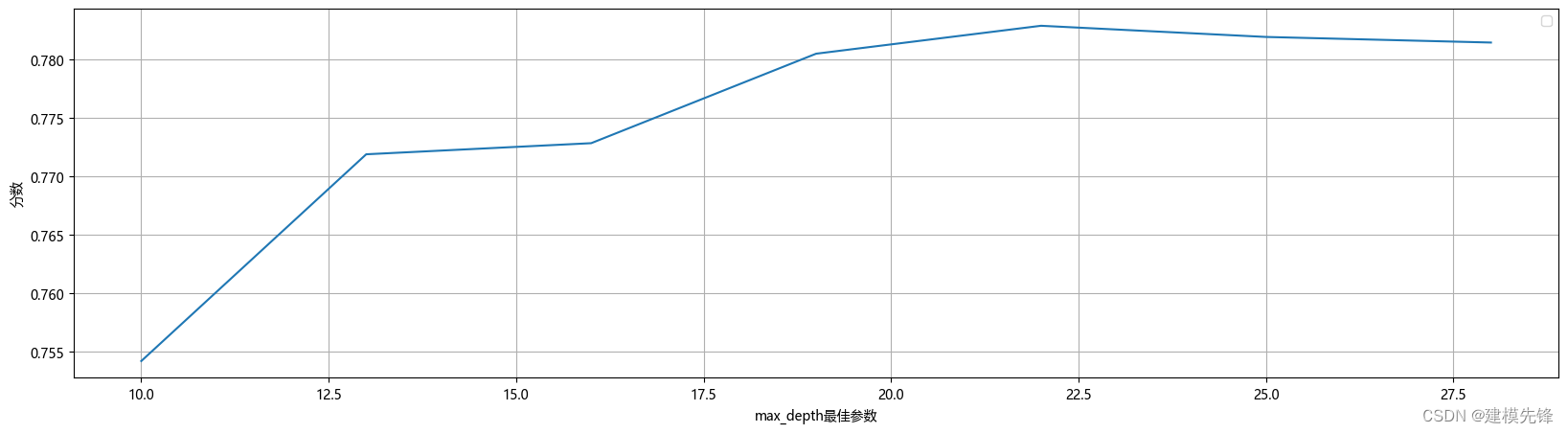

決策樹的深度為22。

網格搜索調參：

通過網格搜索，我們對最終的模型超參數進行分析，得出重要超參數如表所示。采用10折交叉驗證，節點分裂評價準則為基尼系數，決策樹數量為128，內部節點分裂的最小樣本數為2，葉子節點的最小樣本數為1，樹的最大深度為22，葉子節點的最大數量為50。有放回采樣為True，袋外數據測試為False,劃分時考慮的最大特征比例為默認值。

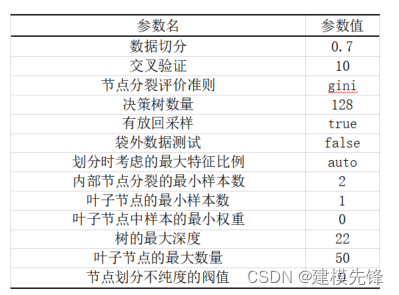
2.4 模型訓練與分類

model = RandomForestClassifier(n_estimators=128,max_depth=22,random_state=1) # min_samples_leaf=11
model.fit(X_train,Y_train)score = model.score(X_test,Y_test)
print('模型分數:',score)
# 計算在訓練集和測試集上的預測均方根誤差
model_lab = model.predict(X_train)
model_pre = model.predict(X_test)
train_mse = mean_squared_error(Y_train,model_lab)
test_mse = mean_squared_error(Y_test,model_pre)
print('訓練數據集上的均方根誤差：',train_mse)
print('測試數據集上的均方根誤差：',test_mse)# 模型使用與評估
y_pred = model.predict(X_test)
print("準確率: %.3f" % accuracy_score(Y_test, y_pred))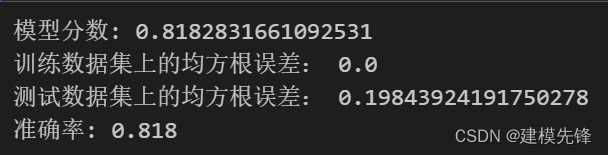

3模型評估

3.1 模型評估結果

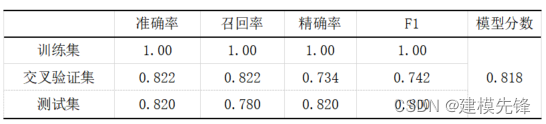
模型評估結果如表所示，表中展示了訓練集和測試集的分類評價指標，通過量化指標來衡量隨機森林對訓練、測試數據的分類效果。準確率：預測正確樣本占總樣本的比例，準確率越大越好；召回率：實際為正樣本的結果中，預測為正樣本的比例，召回率越大越好；精確率：預測出來為正樣本的結果中，實際為正樣本的比例，精確率越大越好；F1：精確率和召回率的調和平均，精確率和召回率是互相影響的，雖然兩者都高是一種期望的理想情況，然而實際中常常是精確率高、召回率就低，或者召回率低、但精確率高。若需要兼顧兩者，那么就可以用F1指標。隨機森林的精確率較高。隨機森林分類模型分數結果為0.818.

3.2 混淆矩陣

# 混淆矩陣
from sklearn.metrics import confusion_matrix
import matplotlib.ticker as tickercm = confusion_matrix(Y_test, y_pred,labels=[0,1,-1])
print('混淆矩陣：\n', cm)
labels=['-1','0','1']
from sklearn.metrics import ConfusionMatrixDisplay
cm_display = ConfusionMatrixDisplay(cm,display_labels=labels).plot()

以熱力圖的形式展示了隨機森林分類模型結果的混淆矩陣

3.3 繪制房價類別三分類的ROC曲線和AUC數值

模型ROC曲線和AUC數值如圖16所示，圖16中的橙色線為參考,即在不使用模型的情況下,Sensitivity 和1-Specificity之比恒等于1。通過繪制ROC曲線,重要的是計算折線下的面積,即圖中的陰影部分,這個面積稱為AUC。在做模型評估時,希望AUC的值越大越好,通常情況下,當AUC在0.8以上時,模型就基本可以接受了。在AUC>0.5的情況下，AUC越接近于1，說明模型效果越好；AUC在 0.5~0.7時有較低準確性，AUC在0.7~0.9時有一定準確性，AUC在0.9以上時有較高準確性；AUC=0.5時，跟隨機猜測一樣，模型沒有分類價值；AUC<0.5時，比隨機猜測還差。然而隨機森林分類模型三種分類的AUC值都在0.90以上,說明模型分類效果明顯，有較高準確性。

3.4 特征重要性可視化

features = X.columns
importances = model.feature_importances_
df = pd.DataFrame()
df['特征'] = features
df['重要性'] = importances
df = df.sort_values('重要性',ascending=False)
# df.iloc[2,1] = df.iloc[2,1]+0.2
xx = df['特征']
yy = df['重要性']
colors = ['darkgreen','gold','red','navy','orange','lime','plum','sienna']
plt.figure(figsize=(15,5))
plt.barh(xx,yy,0.4,color=colors,alpha=0.8)#color參數傳入顏色列表，可以在一幅圖中顯示不同顏色
plt.xlabel('Importance score')
plt.ylabel('variable')
plt.title('RandomForestRegressor')
plt.grid()
plt.show()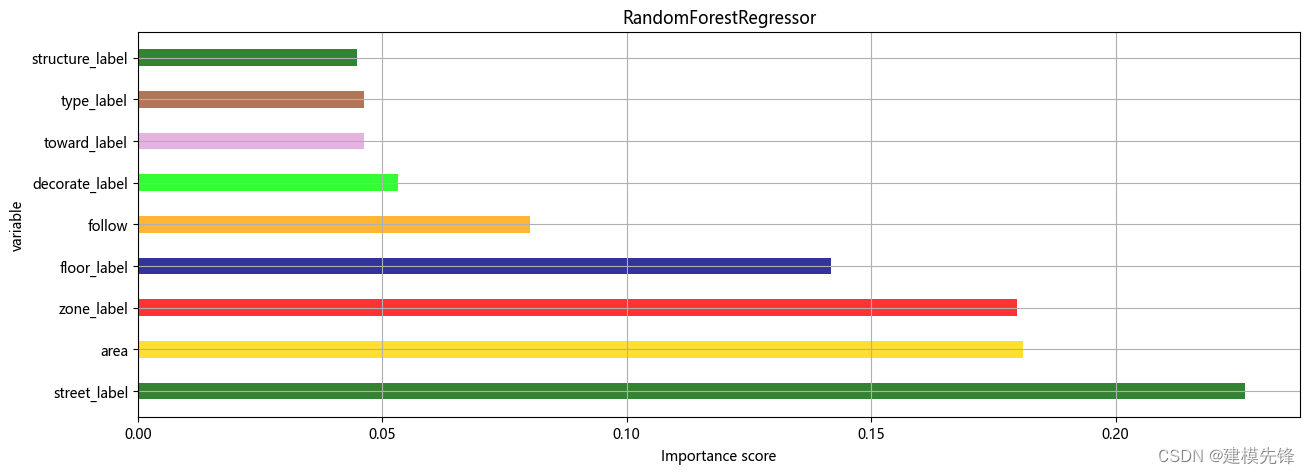

分類標簽對房價的影響中，街道位置對房價的影響重要性最大，區域和建造面積重要性其次，相比較，房子的構造和戶型以及房子朝向對房價的影響重要性較小，裝修、關注度以及樓層層次對房價的影響重要性適中。

總結

通過對宜昌市二手房數據的分析，我們探討了影響房價的重要因素，并對房價進行分類，熟悉了python中numpy和pandas等高級數據處理包的應用，并掌握了數據分析的步驟和流程。經過機器學習中對隨機森林模型的研究，進一步加深了對機器學習的了解，熟悉了隨機森林模型的原理和在python中的使用方法，并加深了對機器學習模型常用評價指標的了解，每種算法都有其各自的優點和使用場景，沒有最好的算法，只有更好的數據。

參考資料

[1]李超.機器學習模型在股票價格時間序列分析中的應用與比較[J].電子世界,2021(09):66-70.

[2]李巖. 基于隨機森林的滬深300預測研究[J]. 品牌研究,2022(2):108-110.