前面我們已經了解了幾大排序了，那么我們今天就來再了解一下剩下的快速排序法，這是一種非常經典的方法，時間復雜度是N*logN。

快速排序法：

基本思想為：任取待排序元素序列中的某元素作為基準值，按照該排序碼將待排序集合分割成兩子序列，左子序列中所有元素均小于基準值，右子序列中所有元素均大于基準值，然后最左右子序列重復該過程，直到所有元素都排列在相應位置上為止。

我們的快速排序可以通過遞歸和非遞歸來實現，我們先來看看遞歸實現快排，我們的遞歸快排又分為三個版本，三種方法各有各的特點，我們接下來就來看看吧。

需要調用的函數代碼：

void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}int GetMidi(int* a, int begin, int end)
{int midi = (begin + end) / 2;// begin midi end 三個數選中位數if (a[begin] < a[midi]){if (a[midi] < a[end])return midi;else if (a[begin] > a[end])return begin;elsereturn end;}else // a[begin] > a[midi]{if (a[midi] > a[end])return midi;else if (a[begin] < a[end])return begin;elsereturn end;}
}

hoare版本單趟排序：

// hoare
int PartSort1(int* a, int begin, int end)
{int midi = GetMidi(a, begin, end);Swap(&a[midi], &a[begin]);int left = begin, right = end;int keyi = begin;while (left < right){// 右邊找小while (left < right && a[right] >= a[keyi]){--right;}// 左邊找大while (left < right && a[left] <= a[keyi]){++left;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);return left;
}

這個版本的單趟排序理解起來很容易，但是我們的坑點比較多，所以難度對于我們而言還是有點挑戰性，我們需要兩個變量來實現，我們的left從左邊數組的首元素開始走，找比keyi位置大的元素，keyi代表的就是我們數組首元素的下標，我們用right從最后一個元素開始走，找比keyi位置小的元素，找到了一個大的元素和一個小的元素就交換，但是我們的數組中可能有多個相等的元素，所以我們內嵌循環就得用<=。我們最后left和right相遇時結束，相遇位置的右邊的元素大于等于keyi位置的元素，而相遇位置左邊的元素都小于等于keyi位置的元素，我們最后就將left位置的元素和keyi位置的元素交換再返回left就完成了。

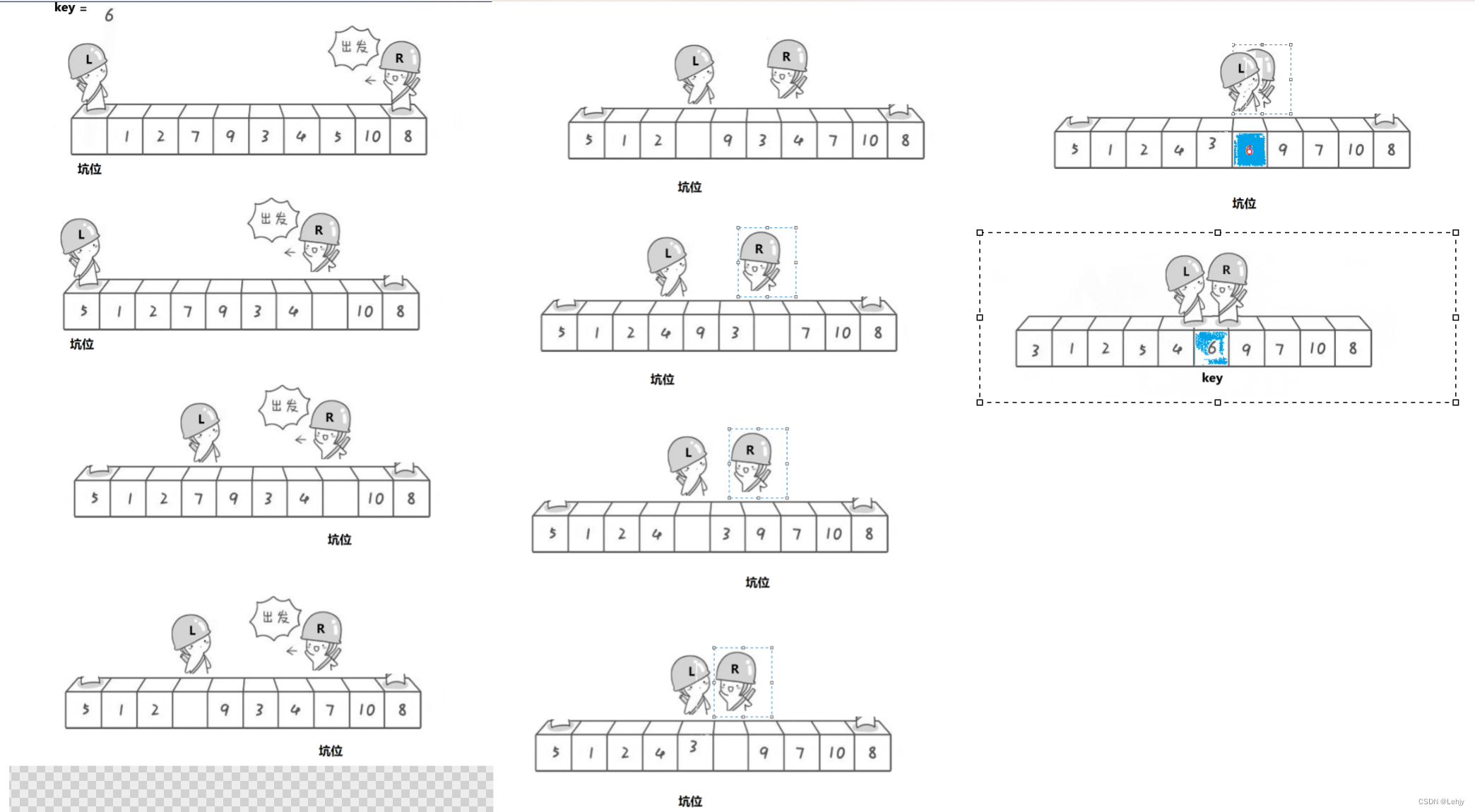
挖坑法單趟排序：

int PartSort2(int* a, int begin, int end)
{int midi = GetMidi(a, begin, end);Swap(&a[midi], &a[begin]);int key = a[begin];int hole = begin;while (begin < end){// 右邊找小，填到左邊的坑while (begin < end && a[end] >= key){--end;}a[hole] = a[end];hole = end;// 左邊找大，填到右邊的坑while (begin < end && a[begin] <= key){++begin;}a[hole] = a[begin];hole = begin;}a[hole] = key;return hole;
}

我們先將第一個數據存放在臨時變量key中形成一個坑位，我們同樣用到left和right，同樣的用法，left從第一個元素往后走，right從最后一個元素往前走。我們的right先走，找到一個比hole下標小的元素就于hole下標的元素交換，交換之后left再走，找到一個比hole位置大的元素就與hole位置的元素交換，然后再left位置形成一個坑點。然后又是right走，交換后left走，反復進行，最后在相遇的時候就結束循環。因為我們的hole下標的值都是空的，所以在最后我們將key的數據給hole下標的坑位就可以了，最后再返回坑位的數據。具體的過程如下圖所示：

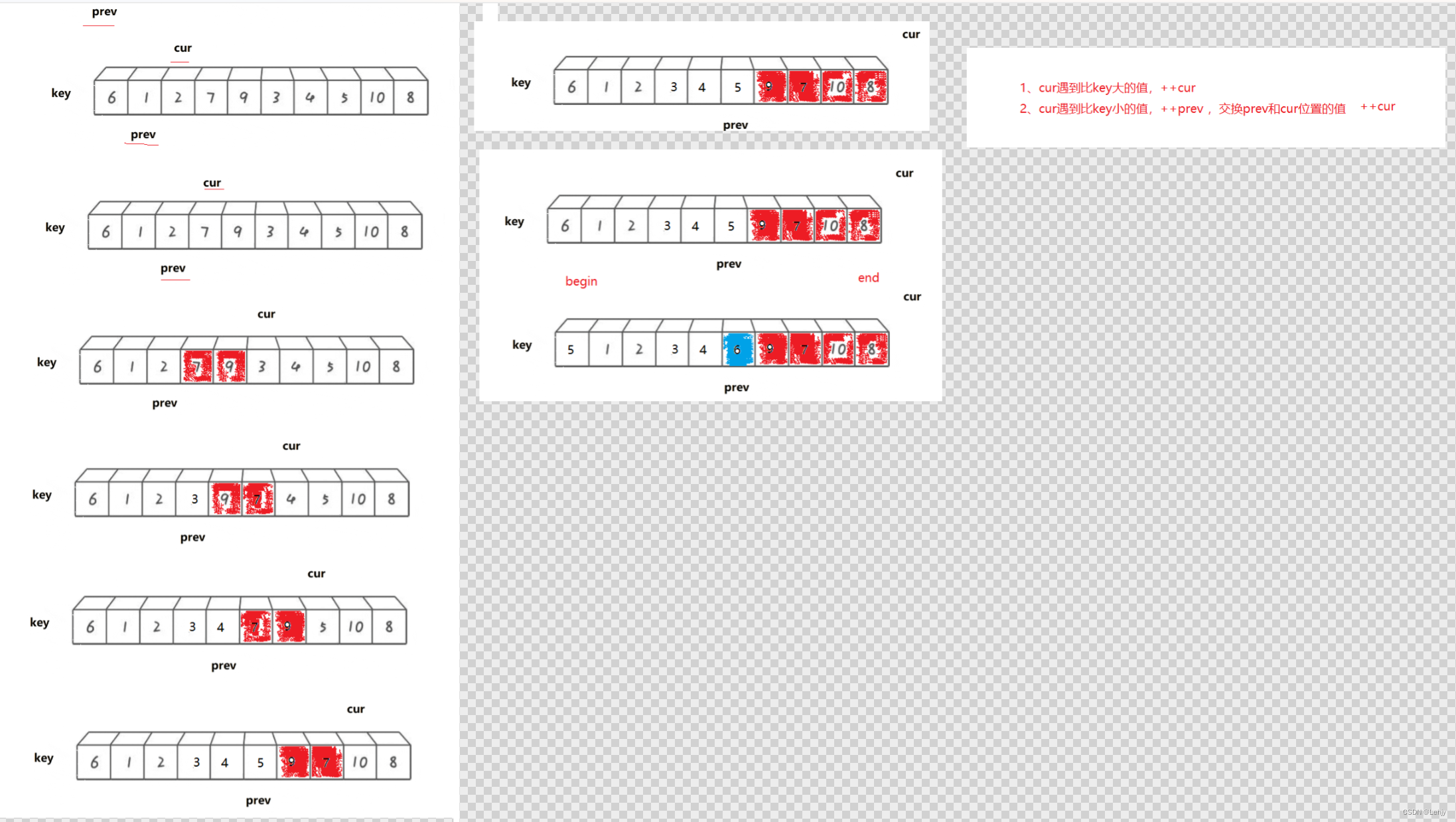
前后指針版本單趟排序：

int PartSort3(int* a, int begin, int end)
{int midi = GetMidi(a, begin, end);Swap(&a[midi], &a[begin]);int keyi = begin;int prev = begin;int cur = prev + 1;while (cur <= end){if (a[cur] < a[keyi] && ++prev != cur)Swap(&a[prev], &a[cur]);++cur;}Swap(&a[prev], &a[keyi]);keyi = prev;return keyi;
}

我們的前后指針版本看起來比前兩個版本更加的容易，因為我們的兩個指針prev指向我們數組首元素的下標，而cur是我們首元素的下一個元素的下標，我們的cur先走，如果我們指向的元素比keyi位置的元素大的話我們就cur++向前走一位，如果比keyi位置的元素小的話我們就prev++向前走一位再與cur位置的交換，cur再繼續往前走知道cur>end的時候就結束循環。最后我們再將prev位置的數據給keyi位置就完成了。

單趟優化版本：

void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;if (end - begin + 1 <= 10){InsertSort(a + begin, end - begin + 1);}else{int midi = GetMidi(a, begin, end);Swap(&a[midi], &a[begin]);int left = begin, right = end;int keyi = begin;while (left < right){// 右邊找小while (left < right && a[right] >= a[keyi]){--right;}// 左邊找大while (left < right && a[left] <= a[keyi]){++left;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);keyi = left;// [begin, keyi-1] keyi [keyi+1, end]QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);}
}

單趟優化版本就是我們的區間數據不大時，我們用直接插入排序法，而數據太大的時候我們就用hoare版本的單趟排序。

函數遞歸實現快排：

void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;int keyi = PartSort2(a, begin, end);QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);
}

實現我們只需要調用一個版本的單趟排序在進行遞歸就可以了。我們代碼中是用的挖坑法的單趟排序，我們就直接調用PartSort2就可以了。

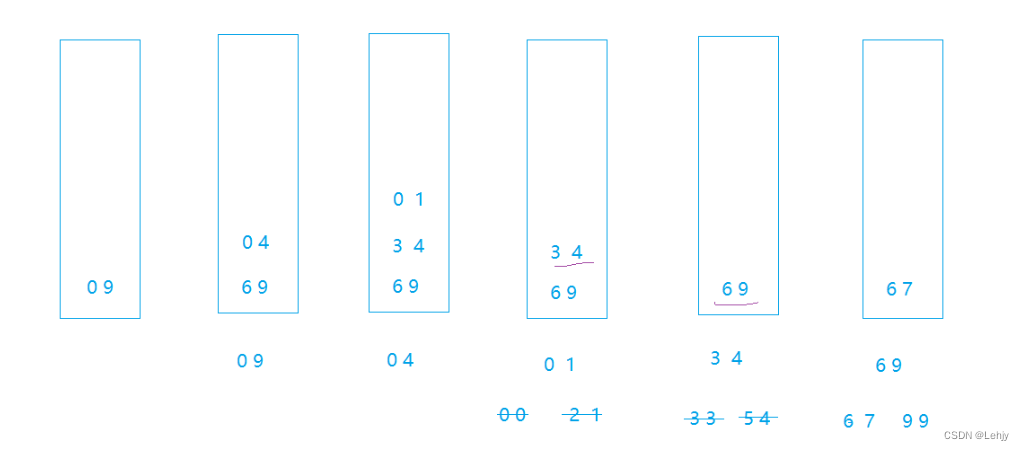
遞歸的我們已經了解完了，那么我們就來看看非遞歸的怎么實現吧：

void QuickSortNonR(int* a, int begin, int end)
{ST s;STInit(&s);STPush(&s, end);STPush(&s, begin);while (!STEmpty(&s)){int left = STTop(&s);STPop(&s);int right = STTop(&s);STPop(&s);int keyi = PartSort3(a, left, right);// [left, keyi-1] keyi [keyi+1, right]if (left < keyi - 1){STPush(&s, keyi - 1);STPush(&s, left);}if (keyi + 1 < right){STPush(&s, right);STPush(&s, keyi + 1);}}STDestroy(&s);
}

非遞歸版本的快速排序。我們需要起始位置 begin 和結束位置 end。首先，函數創建一個棧 st，用于存儲待處理的子數組的起始和結束位置。將 end 和 begin 分別壓入棧中，表示對整個數組進行排序。進入循環，只要棧不為空，從棧中彈出兩個元素，分別賦值給 left 和 right，表示當前要處理的子數組的起始和結束位置。調用 PartSort3 函數對子數組進行分區，得到基準元素的位置 keyi。根據分區的結果，將子數組劃分為 [left, keyi-1]、[keyi]、[keyi+1, right] 三個部分。如果 keyi + 1 < right，說明右側子數組仍然有元素需要排序，將右側子數組的起始位置 keyi + 1 和結束位置 right 壓入棧中。如果 left < keyi - 1，說明左側子數組仍然有元素需要排序，將左側子數組的起始位置 left 和結束位置 keyi - 1 壓入棧中。循環繼續進行，直到棧為空，表示所有子數組都被處理完畢。最后，銷毀棧 st，就完成了非遞歸版本的快速排序。

如果對大家有所幫助的話就支持一下吧！