本文僅供學習使用
本文參考：
B站：DR_CAN

---

1. 定義

$$A\vec{v}=\lambda \vec{v}$$
對于給定線性變換 $A$，特征向量eigenvector $\vec{v}$ 在此變換后仍與原來的方向共線，但長度可能會發生改變，其中 $\lambda$ 為標量，即縮放比例，稱其為特征值eigenvalue

1.1 線性變換

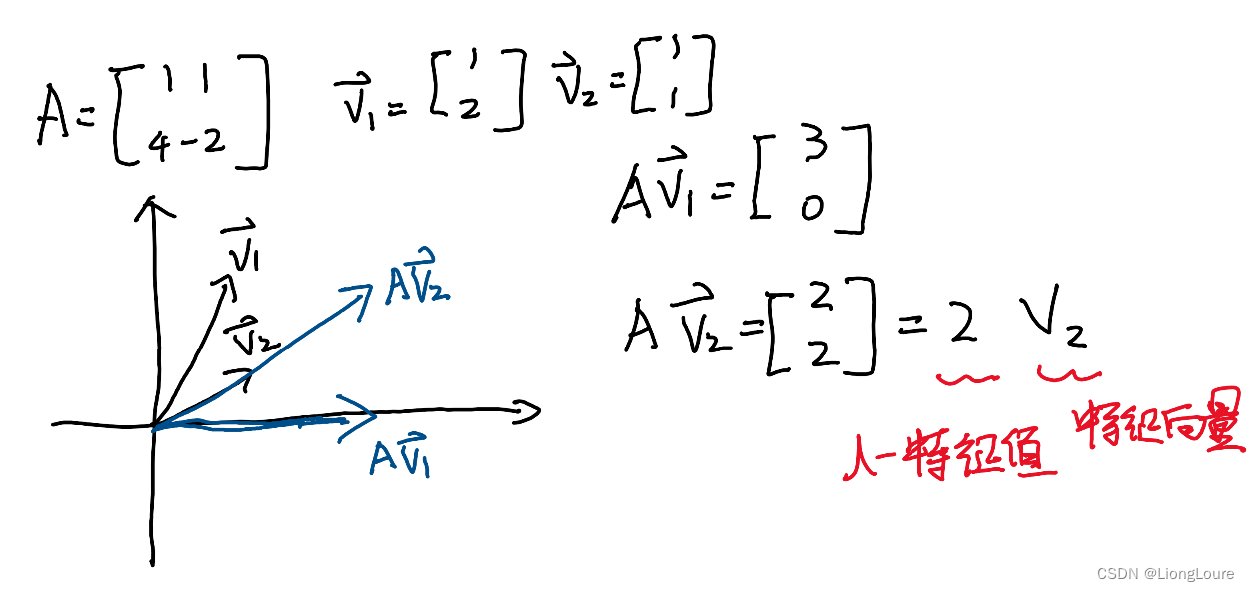
1.2 求解特征值，特征向量

$$A\vec{v}=\lambda \vec{v}?\left(A?\lambda E\right)\vec{v}=0?\left|A?\lambda E\right|=0$$

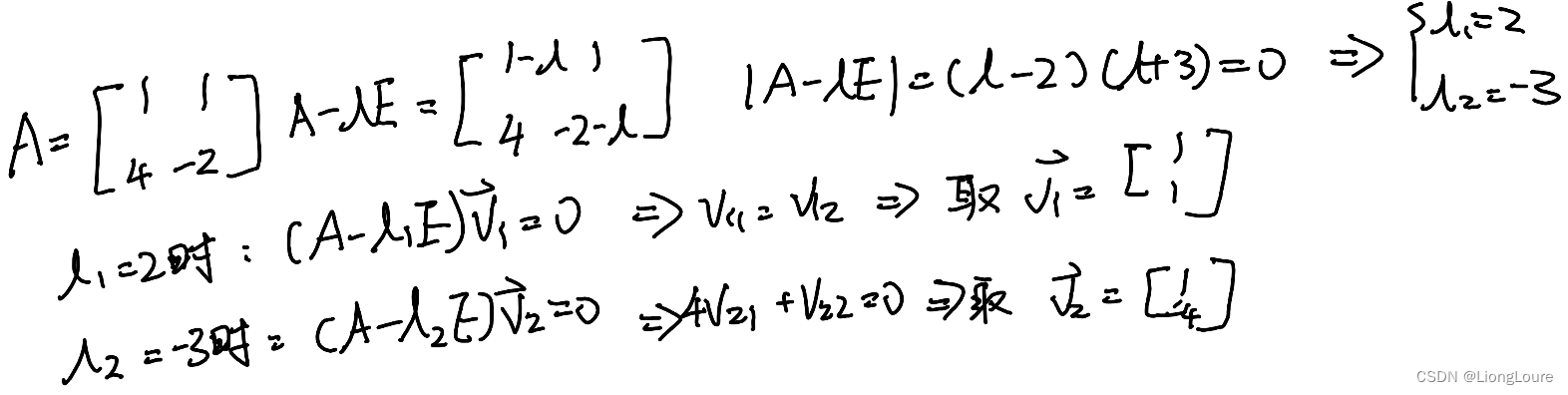
1.3 應用：對角化矩陣——解耦Decouple

$P=\left[{\vec{v}}_1,{\vec{v}}_2\right]$—— coordinate transformation matrix

$$\begin{gathered} AP=A\left[\begin{array}{cc}{\vec{v}}_1& {\vec{v}}_2\end{array}\right]=\left[\begin{array}{cc}A\left[\begin{array}{c}{v}_{11}\\ v_{12}\end{array}\right]& A\left[\begin{array}{c}{v}_{21}\\ v_{22}\end{array}\right]\end{array}\right]=\left[\begin{array}{cc}{\lambda }_1{v}_{11}& {\lambda }_2{v}_{21}\\ {\lambda }_1{v}_{12}& {\lambda }_2{v}_{22}\end{array}\right]=\left[\begin{array}{cc}{v}_{11}& v_{21}\\ v_{12}& v_{22}\end{array}\right]\left[\begin{array}{cc}{\lambda }_1& 0\\ 0& {\lambda }_2\end{array}\right]=P\Lambda \\ ?AP=P\Lambda ?P^{?1}AP=\Lambda \end{gathered}$$

• 微分方程組 state-space rep
  

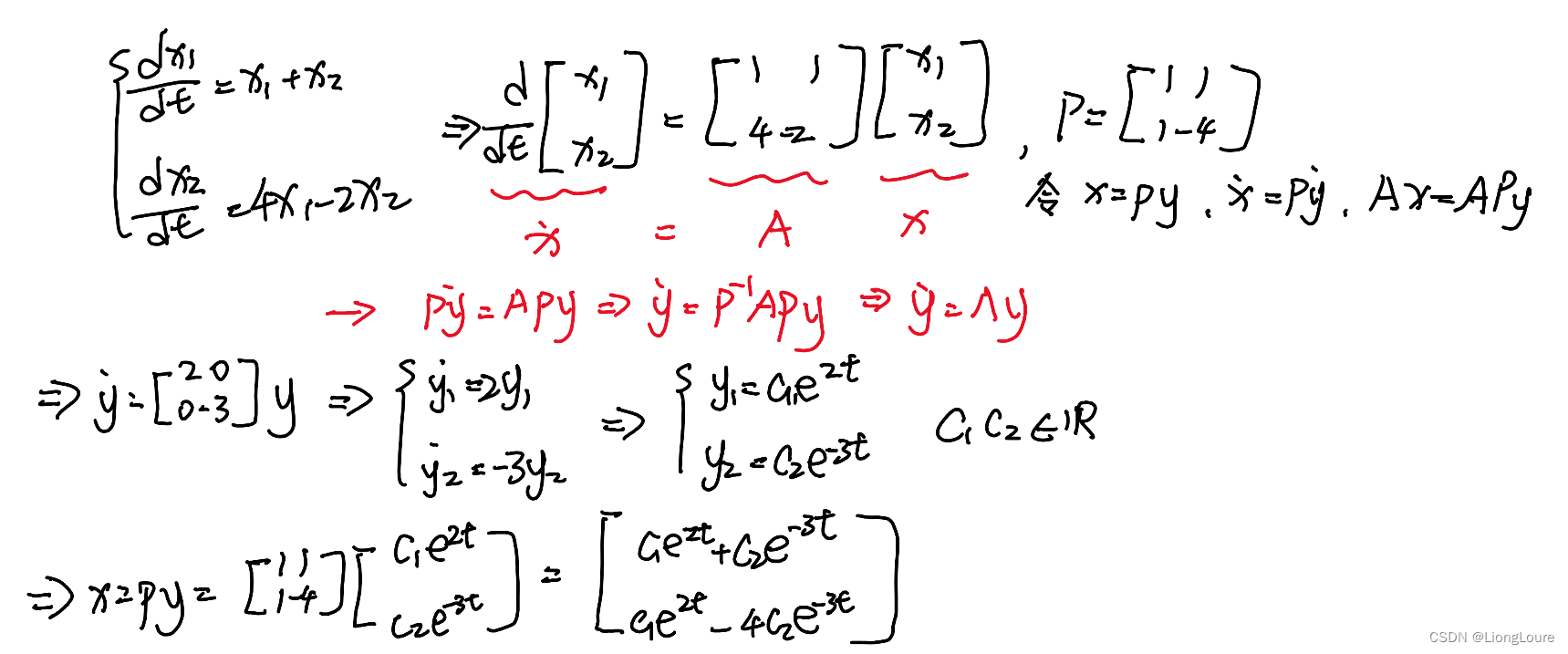
2. Summary

1. $A\vec{v}=\lambda \vec{v}$ 在一條直線上
2. 求解方法： $\left|A?\lambda E\right|=0$
3. $P^{?1}AP=\Lambda ,P=\left[\begin{array}{ccc}{\vec{v}}_1& {\vec{v}}_2& ?\end{array}\right],\Lambda =\left[\begin{array}{ccc}{\lambda }_1& & \\ & {\lambda }_2& \\ & & ?\end{array}\right]$
4. $\dot{x}=Ax,x=Py,\dot{y}=\Lambda y$