java基礎之TreeMap詳解

TreeMap詳解

TreeMap是Map接口的一個實現類，底層基于紅黑樹的實現，按照key的順序存儲

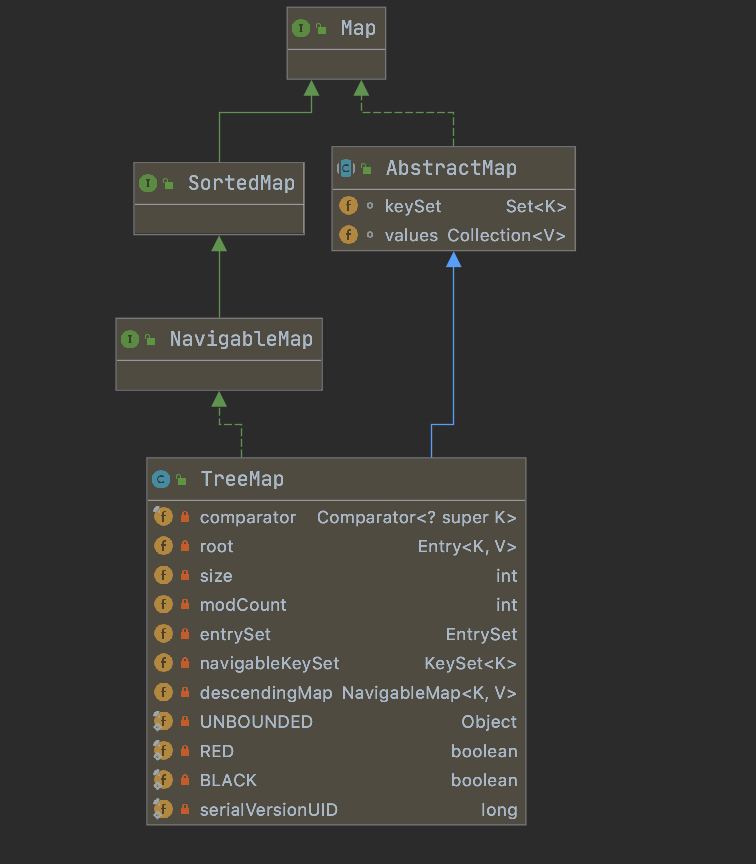
TreeMap
TreeMap

從繼承結構可以看到TreeMap除了繼承了AbstractMap類，還實現了NavigableMap接口，而NavigableMap接口是繼承自SortedMap接口的，所以TreeMap是可以進行排序的

關鍵變量

//?比較器，根據比較器來決定TreeMap的排序，如果為空，按照key做自然排序(最小的在根節點)
private?final?Comparator<??super?K>?comparator;
//?根節點
private?transient?Entry<K,V>?root;

/**
?*?The?number?of?entries?in?the?tree
?*?樹的大小
?*/
private?transient?int?size?=?0;

/**
?*?The?number?of?structural?modifications?to?the?tree.
?*?修改次數
?*/
private?transient?int?modCount?=?0;

//?Entry為TreeMap的內部類
static?final?class?Entry<K,V>?implements?Map.Entry<K,V>?{
????????K?key;
????????V?value;
????????Entry<K,V>?left;
????????Entry<K,V>?right;
????????Entry<K,V>?parent;
????????boolean?color?=?BLACK;
}

構造函數

//?默認空參構造器，比較器設置為空
public?TreeMap()?{
????comparator?=?null;
}
//?提供比較器
public?TreeMap(Comparator<??super?K>?comparator)?{
??this.comparator?=?comparator;
}

public?TreeMap(Map<??extends?K,???extends?V>?m)?{
??comparator?=?null;
??putAll(m);
}

public?TreeMap(SortedMap<K,???extends?V>?m)?{
??comparator?=?m.comparator();
??try?{
????buildFromSorted(m.size(),?m.entrySet().iterator(),?null,?null);
??}?catch?(java.io.IOException?cannotHappen)?{
??}?catch?(ClassNotFoundException?cannotHappen)?{
??}
}

get方法

public?V?get(Object?key)?{
????Entry<K,V>?p?=?getEntry(key);
????return?(p==null???null?:?p.value);
}

final?Entry<K,V>?getEntry(Object?key)?{
??//?Offload?comparator-based?version?for?sake?of?performance
??if?(comparator?!=?null)
????return?getEntryUsingComparator(key);
??//?從這里可以看出TreeMap的key不可以為null
??if?(key?==?null)
????throw?new?NullPointerException();
??@SuppressWarnings("unchecked")
??Comparable<??super?K>?k?=?(Comparable<??super?K>)?key;
??//?獲取根節點
??Entry<K,V>?p?=?root;
??while?(p?!=?null)?{
????//?判斷是根節點的左子樹還是右子樹
????int?cmp?=?k.compareTo(p.key);
????if?(cmp?<?0)
??????p?=?p.left;
????else?if?(cmp?>?0)
??????p?=?p.right;
????else
??????return?p;
??}
??return?null;
}

put方法

public?V?put(K?key,?V?value)?{
????Entry<K,V>?t?=?root;
???//?根節點為null，表示這是第一個元素
????if?(t?==?null)?{
???????//?主要是為了確保key是可排序的類，以及key不能為null
????????compare(key,?key);?//?type?(and?possibly?null)?check
????//?第三個參數為父節點的entry，根節點沒有父節點，所以為null
????????root?=?new?Entry<>(key,?value,?null);
????????size?=?1;
????????modCount++;
????????return?null;
????}
????int?cmp;
????Entry<K,V>?parent;
????//?split?comparator?and?comparable?paths
????Comparator<??super?K>?cpr?=?comparator;
???//?存在比較器的情況
????if?(cpr?!=?null)?{
????????do?{
????????????parent?=?t;
????????????cmp?=?cpr.compare(key,?t.key);
????????????if?(cmp?<?0)
????????????????t?=?t.left;
????????????else?if?(cmp?>?0)
????????????????t?=?t.right;
????????????else
????????????????return?t.setValue(value);
????????}?while?(t?!=?null);
????}
???//?不存在比較器，進行自然排序
????else?{
???????//?key不能為null
????????if?(key?==?null)
????????????throw?new?NullPointerException();
????????@SuppressWarnings("unchecked")
????????????Comparable<??super?K>?k?=?(Comparable<??super?K>)?key;
??????//?do...while是為了找到該key所要存放的位置(找到父節點)
????????do?{
????????????parent?=?t;
????????????cmp?=?k.compareTo(t.key);
????????????if?(cmp?<?0)
????????????????t?=?t.left;
????????????else?if?(cmp?>?0)
????????????????t?=?t.right;
????????????else
????????????????return?t.setValue(value);
????????}?while?(t?!=?null);
????}
????Entry<K,V>?e?=?new?Entry<>(key,?value,?parent);
???//?比父節點小，是左子樹
????if?(cmp?<?0)
????????parent.left?=?e;
????else
????????parent.right?=?e;
???//?插入之后還要進行平衡操作
????fixAfterInsertion(e);
????size++;
????modCount++;
????return?null;
}

private?void?fixAfterInsertion(Entry<K,V>?x)?{
??x.color?=?RED;

??while?(x?!=?null?&&?x?!=?root?&&?x.parent.color?==?RED)?{
????if?(parentOf(x)?==?leftOf(parentOf(parentOf(x))))?{
??????Entry<K,V>?y?=?rightOf(parentOf(parentOf(x)));
??????if?(colorOf(y)?==?RED)?{
????????setColor(parentOf(x),?BLACK);
????????setColor(y,?BLACK);
????????setColor(parentOf(parentOf(x)),?RED);
????????x?=?parentOf(parentOf(x));
??????}?else?{
????????if?(x?==?rightOf(parentOf(x)))?{
??????????x?=?parentOf(x);
??????????rotateLeft(x);
????????}
????????setColor(parentOf(x),?BLACK);
????????setColor(parentOf(parentOf(x)),?RED);
????????rotateRight(parentOf(parentOf(x)));
??????}
????}?else?{
??????Entry<K,V>?y?=?leftOf(parentOf(parentOf(x)));
??????if?(colorOf(y)?==?RED)?{
????????setColor(parentOf(x),?BLACK);
????????setColor(y,?BLACK);
????????setColor(parentOf(parentOf(x)),?RED);
????????x?=?parentOf(parentOf(x));
??????}?else?{
????????if?(x?==?leftOf(parentOf(x)))?{
??????????x?=?parentOf(x);
??????????rotateRight(x);
????????}
????????setColor(parentOf(x),?BLACK);
????????setColor(parentOf(parentOf(x)),?RED);
????????rotateLeft(parentOf(parentOf(x)));
??????}
????}
??}
??root.color?=?BLACK;
}

remove方法

public?V?remove(Object?key)?{
???//?獲取到該key對應的節點?和get相同
????Entry<K,V>?p?=?getEntry(key);
????if?(p?==?null)
????????return?null;

????V?oldValue?=?p.value;
????deleteEntry(p);
????return?oldValue;
}

private?void?deleteEntry(Entry<K,V>?p)?{
??modCount++;
??size--;

??//?If?strictly?internal,?copy?successor's?element?to?p?and?then?make?p
??//?point?to?successor.
??//?存在兩個子樹(左子樹和右子樹)
??if?(p.left?!=?null?&&?p.right?!=?null)?{
????//?找到與p數值最接近的節點(即右子樹的最左葉子節點)
????Entry<K,V>?s?=?successor(p);
????p.key?=?s.key;
????p.value?=?s.value;
????p?=?s;
??}?//?p?has?2?children

??//?Start?fixup?at?replacement?node,?if?it?exists.
??//?找到所要替代的節點
??Entry<K,V>?replacement?=?(p.left?!=?null???p.left?:?p.right);

??if?(replacement?!=?null)?{
????//?Link?replacement?to?parent
????//?替換節點
????replacement.parent?=?p.parent;
????if?(p.parent?==?null)
??????root?=?replacement;
????else?if?(p?==?p.parent.left)
??????p.parent.left??=?replacement;
????else
??????p.parent.right?=?replacement;

????//?Null?out?links?so?they?are?OK?to?use?by?fixAfterDeletion.
????p.left?=?p.right?=?p.parent?=?null;

????//?Fix?replacement
????//?刪除的節點為黑色節點，需要進行平衡
????if?(p.color?==?BLACK)
??????fixAfterDeletion(replacement);
??}?
??//?此時replacement為null(表明?p沒有左子樹也沒有右子樹)，如果p沒有父節點，表明該樹只有一個根節點
??else?if?(p.parent?==?null)?{?//?return?if?we?are?the?only?node.
????root?=?null;
??}?
??//?此時replacement為null(表明?p沒有左子樹也沒有右子樹)，表明該節點為葉子節點
??else?{?//??No?children.?Use?self?as?phantom?replacement?and?unlink.
????//?刪除的節點為黑色節點，需要進行平衡
????if?(p.color?==?BLACK)
??????fixAfterDeletion(p);
??//?將p從樹中移除
????if?(p.parent?!=?null)?{
??????if?(p?==?p.parent.left)
????????p.parent.left?=?null;
??????else?if?(p?==?p.parent.right)
????????p.parent.right?=?null;
??????p.parent?=?null;
????}
??}
}

static?<K,V>?TreeMap.Entry<K,V>?successor(Entry<K,V>?t)?{
??if?(t?==?null)
????return?null;
??else?if?(t.right?!=?null)?{
????//?右節點不為null，找到后繼節點(即右子樹的左葉子節點)
????Entry<K,V>?p?=?t.right;
????while?(p.left?!=?null)
??????p?=?p.left;
????return?p;
??}?else?{
????Entry<K,V>?p?=?t.parent;
????Entry<K,V>?ch?=?t;
????while?(p?!=?null?&&?ch?==?p.right)?{
??????ch?=?p;
??????p?=?p.parent;
????}
????return?p;
??}
}

private?void?fixAfterDeletion(Entry<K,V>?x)?{
??while?(x?!=?root?&&?colorOf(x)?==?BLACK)?{
????if?(x?==?leftOf(parentOf(x)))?{
??????Entry<K,V>?sib?=?rightOf(parentOf(x));

??????if?(colorOf(sib)?==?RED)?{
????????setColor(sib,?BLACK);
????????setColor(parentOf(x),?RED);
????????rotateLeft(parentOf(x));
????????sib?=?rightOf(parentOf(x));
??????}

??????if?(colorOf(leftOf(sib))??==?BLACK?&&
??????????colorOf(rightOf(sib))?==?BLACK)?{
????????setColor(sib,?RED);
????????x?=?parentOf(x);
??????}?else?{
????????if?(colorOf(rightOf(sib))?==?BLACK)?{
??????????setColor(leftOf(sib),?BLACK);
??????????setColor(sib,?RED);
??????????rotateRight(sib);
??????????sib?=?rightOf(parentOf(x));
????????}
????????setColor(sib,?colorOf(parentOf(x)));
????????setColor(parentOf(x),?BLACK);
????????setColor(rightOf(sib),?BLACK);
????????rotateLeft(parentOf(x));
????????x?=?root;
??????}
????}?else?{?//?symmetric
??????Entry<K,V>?sib?=?leftOf(parentOf(x));

??????if?(colorOf(sib)?==?RED)?{
????????setColor(sib,?BLACK);
????????setColor(parentOf(x),?RED);
????????rotateRight(parentOf(x));
????????sib?=?leftOf(parentOf(x));
??????}

??????if?(colorOf(rightOf(sib))?==?BLACK?&&
??????????colorOf(leftOf(sib))?==?BLACK)?{
????????setColor(sib,?RED);
????????x?=?parentOf(x);
??????}?else?{
????????if?(colorOf(leftOf(sib))?==?BLACK)?{
??????????setColor(rightOf(sib),?BLACK);
??????????setColor(sib,?RED);
??????????rotateLeft(sib);
??????????sib?=?leftOf(parentOf(x));
????????}
????????setColor(sib,?colorOf(parentOf(x)));
????????setColor(parentOf(x),?BLACK);
????????setColor(leftOf(sib),?BLACK);
????????rotateRight(parentOf(x));
????????x?=?root;
??????}
????}
??}

??setColor(x,?BLACK);
}

https://zhhll.icu/2021/java基礎/集合/7.TreeMap詳解/

本文由 mdnice 多平臺發布

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/211440.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/211440.shtml
英文地址，請注明出處：http://en.pswp.cn/news/211440.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！

相關文章

使用Vue3+Typescript手寫一個日歷簽到組件

使用Vue3+Typescript手寫一個日歷簽到組件

設計理念 昨天寫了個簡單美觀的日歷簽到組件&#xff0c;使用的是Vue3TypeScript&#xff0c;大概邏輯是先找到本月份第一天是周幾&#xff0c;然后開始填充月份日期&#xff1a;weeksArray:[[]]:之后渲染到表格中&#xff0c;對于簽到事件觸發則先判斷是否是今天且還未沒有簽…
閱讀更多...
【PyTorch】模型訓練過程優化分析

【PyTorch】模型訓練過程優化分析

文章目錄 1. 模型訓練過程劃分1.1. 定義過程1.1.1. 全局參數設置1.1.2. 模型定義 1.2. 數據集加載過程1.2.1. Dataset類&#xff1a;創建數據集1.2.2. Dataloader類&#xff1a;加載數據集 1.3. 訓練循環 2. 模型訓練過程優化的總體思路2.1. 提升數據從硬盤轉移到CPU內存的效率…
閱讀更多...
SPRD Android 13 需要在設置--顯示--鎖定屏幕--雙行時鐘--＜關閉＞

SPRD Android 13 需要在設置--顯示--鎖定屏幕--雙行時鐘--＜關閉＞

開始去改默認值沒生效 --- a/frameworks/base/packages/SettingsProvider/res/values/defaults.xml +++ b/frameworks/base/packages/SettingsProvider/res/values/defaults.xml @@ -336,4 +336,6 @@<integer name="def_navigation_bar_config">0</integer…
閱讀更多...
西南科技大學數字電子技術實驗三（MSI邏輯器件設計組合邏輯電路及FPGA的實現）FPGA部分

西南科技大學數字電子技術實驗三（MSI邏輯器件設計組合邏輯電路及FPGA的實現）FPGA部分

一、實驗目的 進一步掌握MIS（中規模集成電路）設計方法。通過用MIS譯碼器、數據選擇器實現電路功能，熟悉它們的應用。進一步學習如何記錄實驗中遇到的問題及解決方法。二、實驗原理 1、4位奇偶校驗器 Y=S7i=0DiMi D0=D3=D5=D6=D D1=D2=D4=D7= `D 2、組合邏輯電路 F=A`B C …
閱讀更多...
面試計算機網絡八股文五問五答第二期

面試計算機網絡八股文五問五答第二期

面試計算機網絡八股文五問五答第二期 作者&#xff1a;程序員小白條&#xff0c;個人博客 相信看了本文后&#xff0c;對你的面試是有一定幫助的&#xff01; ?點贊?收藏?不迷路&#xff01;? 1.OSI七層協議&#xff1f; 2. TCP和UDP傳輸協議的區別&#xff1f; TCP是可…
閱讀更多...
C語言_常見位操作

C語言_常見位操作

C語言_常見位操作 文章目錄 C語言_常見位操作一、位操作函數二、代碼示例 一、位操作函數 設置某位為1或者對某位清0、獲取某位的值、對某位取反 /*對某位置1*/ unsigned Setbit(unsigned x,int n) {return x | 1 << n; }/*對某位清0*/ unsigned Resetbit(unsigned x,…
閱讀更多...
為什么要用向量檢索

為什么要用向量檢索

之前寫過一篇文章&#xff0c;是我個人到目前階段的認知&#xff0c;所做的判斷。我個人是做萬億級數據的搜索優化工作的。一直在關注任何和搜索相關的內容。 下一代搜索引擎會什么&#xff1f;-CSDN博客 這篇文章再來講講為什么要使用向量搜索。 在閱讀這篇文章之前呢&#xf…
閱讀更多...
【網絡安全】網絡設備可能面臨哪些攻擊？

【網絡安全】網絡設備可能面臨哪些攻擊？

網絡設備通常是網絡基礎設施的核心&#xff0c;并控制著整個網絡的通信和安全&#xff0c;同樣面臨著各種各樣的攻擊威脅。 對網絡設備的攻擊一旦成功&#xff0c;并進行暴力破壞&#xff0c;將會導致網絡服務不可用&#xff0c;且可以對網絡流量進行控制&#xff0c;利用被攻陷…
閱讀更多...
【JavaEE】線程池

【JavaEE】線程池

作者主頁&#xff1a;paper jie_博客 本文作者&#xff1a;大家好&#xff0c;我是paper jie&#xff0c;感謝你閱讀本文&#xff0c;歡迎一建三連哦。 本文于《JavaEE》專欄&#xff0c;本專欄是針對于大學生&#xff0c;編程小白精心打造的。筆者用重金(時間和精力)打造&…
閱讀更多...
springcloud分布式事務

springcloud分布式事務

文章目錄 一.為什么引入分布式事務?二.理論基礎1.CAP定理2.BASE理論 三.Seata1.微服務集成Seata2.XA模式(掌握)3.AT模式(重點)4.TCC模式(重點)5.Saga模式(了解) 四.四種模式對比五.Seata高可用 一.為什么引入分布式事務? 事務的ACID原則 在大型的微服務項目中,每一個微服務都…
閱讀更多...
案例課4——智齒客服

案例課4——智齒客服

1.公司介紹 智齒科技&#xff0c;一體化客戶聯絡中心解決方案提供商。提供基于「客戶聯絡中心」場景的一體化解決方案&#xff0c;包括公域私域、營銷服務、軟件BPO的三維一體化。 智齒科技不斷整合前沿的人工智能及大數據技術&#xff0c;已構建形成呼叫中心、機器人「在線語音…
閱讀更多...
Python中函數的遞歸調用

Python中函數的遞歸調用

函數調用自己的編程方式被稱為函數的遞歸調用。遞歸通常能夠將一個大型的復雜問題的遞歸條件&#xff0c;一層一層的回溯到終止條件&#xff0c;然后再根據終止條件的運算結果&#xff0c;一層一層的遞進運算到滿足全部的遞歸條件。它能夠使用少量程序描述出解題過程中的重復運…
閱讀更多...
主機訪問Android模擬器網絡服務方法

主機訪問Android模擬器網絡服務方法

0x00 背景 因為公司的一個手機app的開發需求&#xff0c;要嘗試鏈接手機開啟的web服務。于是在Android Studio的Android模擬器上嘗試連接&#xff0c;發現谷歌給模擬器做了網絡限制&#xff0c;不能直接連接。當然這個限制似乎從很久以前就存在了。一直沒有注意到。 0x01 And…
閱讀更多...
分銷電商結算設計

分銷電商結算設計

概述 分銷電商中涉及支付與結算&#xff1b;支付職責是收錢&#xff0c;結算則是出錢給各利益方&#xff1b; 結算核心圍繞業務模式涉及哪些費用&#xff0c;以及這些費用什么時候通過什么出資渠道&#xff0c;由誰給到收方利益方&#xff1b; 結算要素組成費用項結算周期出…
閱讀更多...
區塊鏈的可拓展性研究【03】擴容整理

區塊鏈的可拓展性研究【03】擴容整理

為什么擴容&#xff1a;在layer1上&#xff0c;交易速度慢&#xff0c;燃料價格高 擴容的目的&#xff1a;在保證去中心化和安全性的前提下&#xff0c;提升交易速度&#xff0c;更快確定交易&#xff0c;提升交易吞吐量&#xff08;提升每秒交易量&#xff09; 目前方案有&…
閱讀更多...
詳解進程管理（銀行家算法、死鎖詳解）

詳解進程管理（銀行家算法、死鎖詳解）

處理機是計算機系統的核心資源。操作系統的功能之一就是處理機管理。隨著計算機的迅速發展&#xff0c;處理機管理顯得更為重要&#xff0c;這主要由于計算機的速度越來越快&#xff0c;處理機的充分利用有利于系統效率的大大提高&#xff1b;處理機管理是整個操作系統的重心所…
閱讀更多...
前后端聯調神器《OpenAPI-Codegen》

前后端聯調神器《OpenAPI-Codegen》

在后端開發完接口之后&#xff0c;前端如果再去寫一遍接口來聯調的話&#xff0c;會很浪費時間&#xff0c;這個時候使用OpenAPI接口文檔來生成Axios接口代碼的話&#xff0c;會大大提高我們的開發效率。 Axios引入 Axios是一個基于Promise的HTTP客戶端&#xff0c;用于瀏覽器…
閱讀更多...
Go壓測工具

Go壓測工具

前言 在做Go的性能分析調研的時候也使用到了一些壓測方面的工具&#xff0c;go本身也給我們提供了BenchMark性能測試用例&#xff0c;可以很好的去測試我們的單個程序性能&#xff0c;比如測試某個函數&#xff0c;另外還有第三方包go-wrk也可以幫助我們做http接口的性能壓測&…
閱讀更多...
C# 任務并行類庫Parallel調用示例

C# 任務并行類庫Parallel調用示例

寫在前面 Task Parallel Library 是微軟.NET框架基礎類庫&#xff08;BCL&#xff09;中的一個&#xff0c;主要目的是為了簡化并行編程&#xff0c;可以實現在不同的處理器上并行處理不同任務&#xff0c;以提升運行效率。Parallel常用的方法有For/ForEach/Invoke三個靜態方法…
閱讀更多...
Element-UI定制化Tree 樹形控件

Element-UI定制化Tree 樹形控件

1.復制 說明&#xff1a;復制Tree樹形控件。 <script> export default {data() {return {data: [{label: 一級 1,children: [{label: 二級 1-1,children: [{label: 三級 1-1-1}]}]}, {label: 一級 2,children: [{label: 二級 2-1,children: [{label: 三級 2-1-1}]}, {l…
閱讀更多...
最新文章

Copyright @ 2022~2023