?????????LRU的設計與實現

一、理解LRU的原理

?LeetCode146:運用你所掌握的數據結構，設計和實現一個LRU(最近最少使用)緩存機制

實現LRUCache類：
LRUCache(int capacity) 以正整數作為容量capacity初始化 LRU 緩存
int get(int key) 如果關鍵字key存在于緩存中，則返回關鍵字的值，否則返回-1
void put(int key,int value) 如果關鍵字已經存在，則變更其數據值；如果關鍵字不存在，則插入該組[關鍵字-值]。當緩存容量達到上限時，它應該在寫入新數據之前刪除最久未使用的數據值，從而為新的數據值留出空間
進階：你是否可以在O(1)時間復雜度內完成這兩種操作？
輸入
["LRUCache","put","put","get","put","get","put","get","get","get"]
[[2],[1,1],[2,2],[1],[3,3],[2],[4,4],[1],[3],[4]]
輸出
[nu1l,nu1l,nu11,1,nu1l,-1,nu1,-1,3,4]
解釋
LRUCache lRUCache new LRUCache(2);
lRUCache.put(1,1);//緩存是{1=1}
lRUCache.put(2,2);//緩存是{1=1,2=2}
lRUCache.get(1);//返回1
lRUCache.put(3,3);//該操作會使得關鍵字2作廢，緩存是{1=1,3=3}
lRUCache.get(2);//返回-1（未找到)
lRUCache.put(4,4);//該操作會使得關鍵字1作廢，緩存是{4=4,3=3}
lRUCache.get(1);//返回-1（未找到)
lRUCache.get(3);//返回3
lRUCache.get(4);//返回4

?關于什么是LRU,簡單來說就是當內存空間滿了，不得不淘汰某些數據時（通常是容量已滿），選擇最久未被使用的數據進行淘汰。
?這里做了簡化，題目讓我們實現一個容量固定的LRUCache。如果插入數據時，發現容器已滿時，則先按照LRU規則淘汰一個數據，再將新數據插入，其中「插入」和「查詢」都算作一次“使用”。
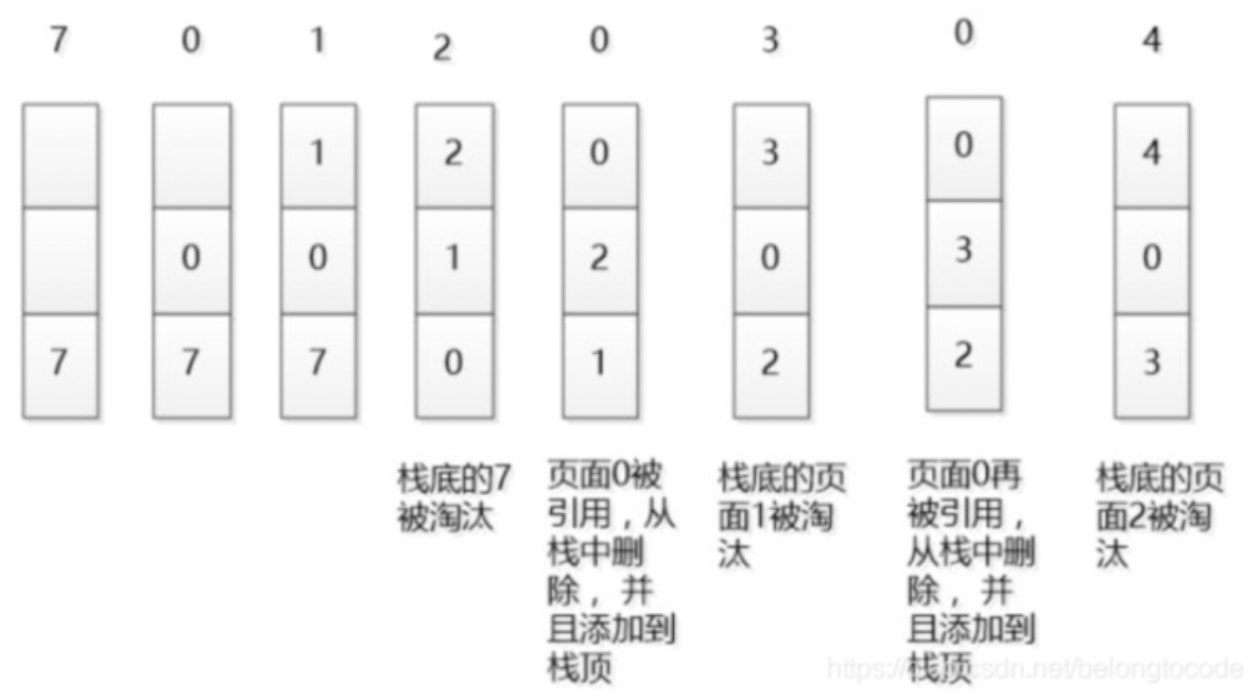
最近最少使用算法(LRU)是大部分操作系統為最大化頁面命中率而廣泛采用的一種頁面置換算法。該算法的思路是，發生缺頁中斷時，選擇未使用時間最長的頁面置換出去。假設內存只能容納3個頁大小，按照7 0 1 2 0 3 0 4的次序訪問頁。假設內存按照棧的方式來描述訪問時間，在上面的，是最近訪問的，在下面的是，最遠時間訪問的，LRU就是這樣工作的：

二、hash+雙向鏈表實現LRU

?目前公認最合理的方式是使用ash+雙向鏈表。想不到吧，接下來我們就看看該怎么做。
Hash的作用是用來做到O(1)訪問元素，哈希表就是普通的哈希映射(HashMap)，通過緩存數據的鍵映射到其在雙向鏈表中的位置。Hash里的數據是key-value結構。value就是我們自己封裝的node,key則是鍵值，也就是在Hash的地址。
?雙向鏈表用來實現根據訪問情況對元素進行排序。雙向鏈表按照被使用的順序存儲了這些鍵值對，靠近頭部的鍵值對是最近使用的，而靠近尾部的鍵值對是最久未使用的。
這樣以來，我們要確認元素的位置直接訪問哈希表就行了，找出緩存項在雙向鏈表中的位置，隨后將其移動到雙向鏈表的頭部，即可在O(1)的時間內完成get或者put操作。具體的方法如下：
1.對于get操作，首先判斷key是否存在：
(1)如果key不存在，則返回-1；
(2)如果key存在，則key對應的節點是最近被使用的節點。通過哈希表定位到該節點在雙向鏈表中的位置，并將其移動到雙向鏈表的頭部，最后返回該節點的值。
2.對于put操作，首先判斷key是否存在：
(1)如果key不存在，使用key和value創建一個新的節點，在雙向鏈表的頭部添加該節點，并將key和該節點添加進哈希表中。然后判斷雙向鏈表的節點數是否超出容量，如果超出容量，則刪除雙向鏈表的尾部節點，并刪除哈希表中對應的項；
(2)如果key存在，則與get操作類似，先通過哈希表定位，再將對應的節點的值更新為value,并將該節點移到雙向鏈表的頭部。
?上述各項操作中，訪問哈希表的時間復雜度為O(1),在雙向鏈表的頭部添加節點、在雙向鏈表的尾部刪除節點的復雜度也為O(1)。而將一個節點移到雙向鏈表的頭部，可以分成[刪除該節點]和[在雙向鏈表的頭部添加節點]兩步操作，都可以在O(1)時間內完成。
?同時為了方便操作，在雙向鏈表的實現中，使用一個偽頭部(dummy head)和偽尾部(dummy tail)標記界限，這樣在添加節點和刪除節點的時候就不需要檢查相鄰的節點是否存在。
?來看一個容量為3的例子，首先緩存了1，此時結構如圖所示。之后再緩存2和3，結構如b所示。

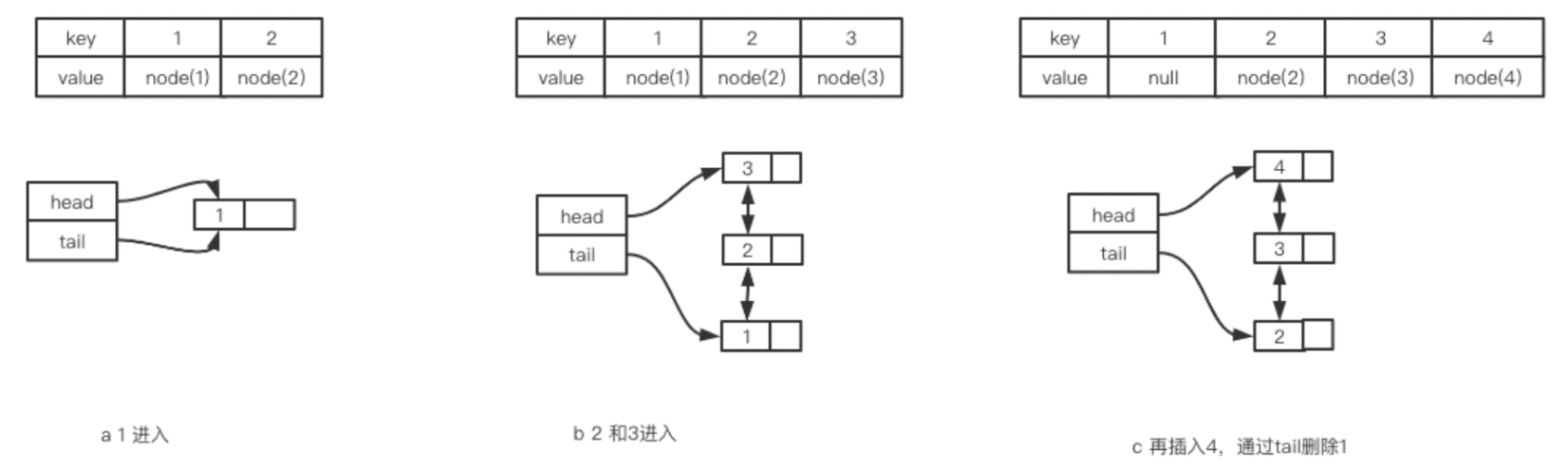
?之后4再進入，此時容量已經不夠了，只能將最遠未使用的元素1刪掉，然后將4插入到鏈表頭部。此時就變成了上圖c的樣子。
?接下來假如又訪問了一次2，會怎么樣呢？此時會將2移動到鏈表的首部，也就是下圖d的樣子。

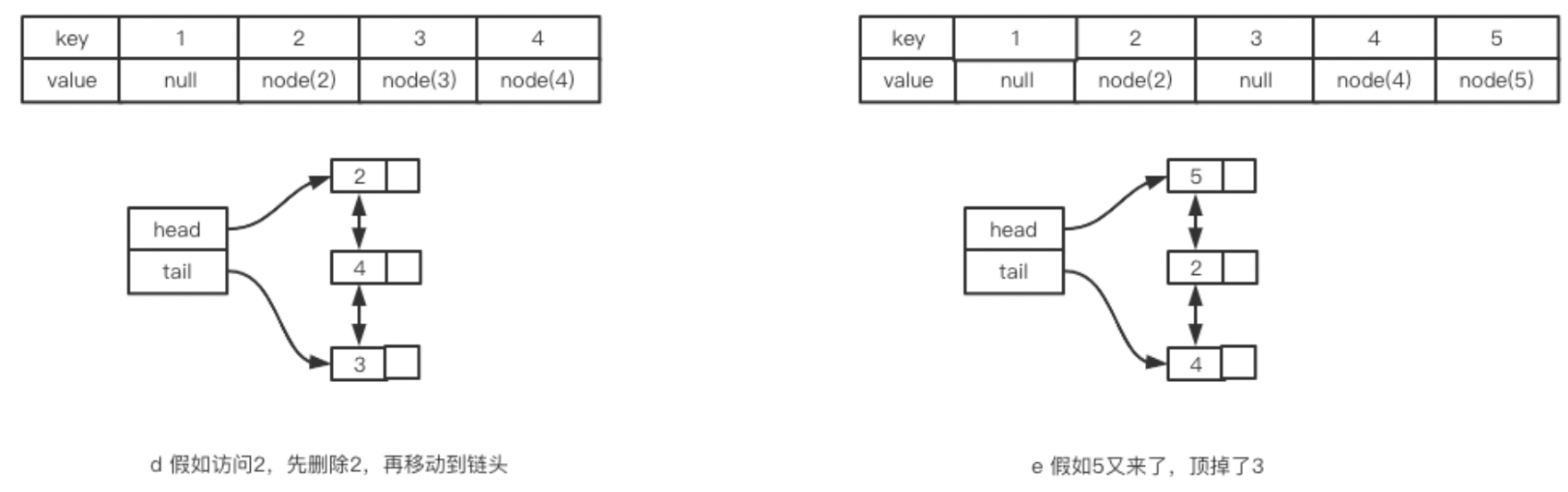
?之后假如又要緩存5呢？此時就將tail指向的3刪除，然后將5插入到鏈表頭部。也就是上圖e的樣子。上面的方案要實現是非常容易的，我們注意到鏈表主要執行幾個操作：
1假如容量沒滿，則將新元素直接插入到鏈表頭就行了。
2.如果容量夠了，新的元素到來，則將tail指向的表尾元素刪除就行了。
3.假如要訪問已經存在的元素，則此時將該先從鏈表中刪除，再插入到表頭就行了。
再看Hash的操作：
1.Hash沒有容量的限制，凡是被訪問的元素都會在Hash中有個標記，key就是我們的查詢條件，而value就是鏈表的結點的引用，可以不用訪問鏈表直接定位到某個結點，然后就可以執行我們在上一節提到的方法來刪除對應的結點。
2.這里雙向鏈表的刪除好理解，那HashMap中是如何刪除的呢？其實就是將node變成為null。這樣get(key)的時候返回的是null,就實現了刪除的功能。
?上述各項操作中，訪問哈希表的時間復雜度為O(),在雙向鏈表的頭部添加節點、在雙向鏈表的尾部刪除節點的復雜度也為O()。而將一個節點移到雙向鏈表的頭部，可以分成「刪除該節點」和「在雙向鏈表的頭部添加節點」兩步操作，都可以在O(1)時間內完成。

public class LRUCache {class DLinkedNode {int key;int value;DLinkedNode prev;DLinkedNode next;public DLinkedNode() {}public DLinkedNode(int _key, int _value) {key = _key; value = _value;}}private Map<Integer, DLinkedNode> cache = new HashMap<Integer, DLinkedNode>();private int size;private int capacity;private DLinkedNode head, tail;public LRUCache(int capacity) {this.size = 0;this.capacity = capacity;// 使用偽頭部和偽尾部節點head = new DLinkedNode();tail = new DLinkedNode();head.next = tail;tail.prev = head;}public int get(int key) {DLinkedNode node = cache.get(key);if (node == null) {return -1;}// 如果 key 存在，先通過哈希表定位，再移到頭部moveToHead(node);return node.value;}public void put(int key, int value) {DLinkedNode node = cache.get(key);if (node == null) {// 如果 key 不存在，創建一個新的節點DLinkedNode newNode = new DLinkedNode(key, value);// 添加進哈希表cache.put(key, newNode);// 添加至雙向鏈表的頭部addToHead(newNode);++size;if (size > capacity) {// 如果超出容量，刪除雙向鏈表的尾部節點DLinkedNode tail = removeTail();// 刪除哈希表中對應的項cache.remove(tail.key);--size;}}else {// 如果 key 存在，先通過哈希表定位，再修改 value，并移到頭部node.value = value;moveToHead(node);}}private void addToHead(DLinkedNode node) {node.prev = head;node.next = head.next;head.next.prev = node;head.next = node;}private void removeNode(DLinkedNode node) {node.prev.next = node.next;node.next.prev = node.prev;}private void moveToHead(DLinkedNode node) {removeNode(node);addToHead(node);}private DLinkedNode removeTail() {DLinkedNode res = tail.prev;removeNode(res);return res;}
}

測試類

public static void main(String[] args){
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1,1);//緩存是{1=1}
lRUCache.put(2,2);//緩存是{1=1,2=2}
System.out.println(lRUCache.get(1));//返回1
lRUCache.put(3,3);//該操作會使得關鍵字2作廢，緩存是{1=1,3=3}
System.out.println(lRUCache.get(2));//返回-1（未找到)
lRUCache.put(4,4);//該操作會使得關鍵字1作廢，緩存是{4=4,3=3}
System.out.println(lRUCache.get(1));//返回-1（未找到)
System.out.println(lRUCache.get(3));//返回3
System.out.println(lRUCache.get(4));//返回4
}