大家好啊，我是董董燦。

最近在寫《計算機視覺入門與調優》（右鍵，在新窗口中打開鏈接）的小冊，其中一部分說到激活函數的時候，談到了神經網絡的非線性問題。

今天就一起來看看，為什么神經網絡需要非線性，或者說為什么它是一個非線性系統。

1、線性系統是什么樣的

先看一個基礎知識：線性函數，這是我們在初中就學過的知識點。

假設有一個線性函數：y = kx + b, 這個函數畫出來是下面的樣子，也就是說， y 和 x 是線性關系。

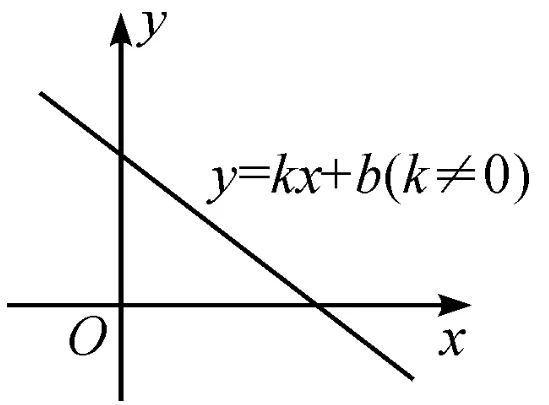
而這個時候如果又有一個線性函數 z = hy + d，那么，我們可以推斷出，變量 z 和 x 同樣也是線性關系。

為什么呢? 可以通過下面的變換得到。

z = hy + d

? ?= z(kx + b) + d

? ?= zk x + zb + d

? ?= zk(x) + (zb + d)

令 zk = K， zb + d = B，那么 z 和 x 的關系就可以寫出 z = Kx + B

所以，z 和 x 同樣是線性關系。

這里想說的一個原理是：多個線性系統的疊加，最終還會是線性系統。

2、神經網絡是什么系統呢？

回到神經網絡，我們知道卷積的算法公式是 y = x * w,，其中 x 是輸入數據，w 是權值，中間的 * 代表卷積計算。關于卷積可以查看：5分鐘搞懂卷積。

那么x * w 是線性關系還是非線性關系呢？不好意思，就是線性關系。

這是因為卷積的核心計算是乘累加運算，所以，卷積算法也是線性的。

假設神經網絡是由大量的卷積算法一層接著一層組成。如果沒有非線性因素的引入，那么在數學模型上，這個大的卷積堆砌的模型就會退化成一個簡單的線性模型，這就使得多層卷積失去了意義。

層數再多也沒用，因為數學上等價于一個卷積，看下圖解釋的更清楚一些。

這就是原因所在。

所以在很多神經網絡模型中，都需要引入非線性因素，從而使得神經網絡模型可以擬合成更加復雜多變的非線性系統。

這樣模型就可以處理復雜的任務，而不用擔心模型在數學上僅僅是一個簡單的線性模型了。

怎么引入非線性因素呢？

最常見的方法就是在卷積層后面增加一層非線性的激活層，這也是為什么在很多卷積算法后面，都能看到 relu 函數的原因。

延伸閱讀，請參考：神經網絡的非線性思想，真的神了。