對無向圖進行鄰接矩陣的轉化，并且利用DFS（深度優先）和BFS（廣度優先）算法進行遍歷輸出，在鄰接矩陣存儲結構上，完成最小生成樹的操作。

一實驗目的

1．掌握圖的相關概念。

2．掌握用鄰接矩陣和鄰接表的方法描述圖的存儲結構。

3．掌握圖的深度優先搜索和廣度優先搜索遍歷的方法及其計算機的實現。

4．理解最小生成樹的有關算法

二實驗內容及要求

實驗內容：

選擇鄰接矩陣或鄰接鏈表存儲結構，掌握圖的創建、遍歷、最小生成樹、拓撲排序、關鍵路徑、最短路徑等典型操作。

編程實現如下功能：

（1）輸入無向圖的頂點數、邊數及各條邊的頂點對，建立用鄰接矩陣表示的無向圖。

（2）對圖進行深度優先搜索和廣度優先搜索遍歷，并分別輸出其遍歷序列。

（3）在鄰接矩陣存儲結構上，完成最小生成樹的操作。

實驗要求：

1.鍵盤輸入數據；

2.屏幕輸出運行結果。

3.要求記錄實驗源代碼及運行結果。

4.運行環境：CodeBlocks/Dev c++/VC6.0等C編譯環境

三實驗過程及運行結果

實驗一：對無向圖進行鄰接矩陣的轉化，并且利用DFS和BFS算法進行遍歷輸出，在鄰接矩陣存儲結構上，完成最小生成樹的操作。

一算法設計思路

包含七個功能函數和一個主函數：void initialMatrix(Graph *g,int n)、void CreatMatrix(Graph *g,int startPoint,int endPoint)、void InputEdge(Graph* g, int n)、void OutputMatrix(Graph g,int n)、void DFSTravers(Graph &g,int i)、void BFSTraverse(Graph &g)、void primMST(Graph* graph)

void initialMatrix(Graph *g,int n)：這個函數是一個用于初始化圖的鄰接矩陣的函數。使用兩個嵌套的循環遍歷鄰接矩陣的每個元素。在每次循環中，將矩陣中的元素賦值為 0，表示該位置上的邊不存在。在外層循環中，將圖結構中的頂點數組 g->vex 的每個元素賦值為 1，表示該頂點存在。

void CreatMatrix(Graph *g,int startPoint,int endPoint)：這段函數是一個用于創建圖的鄰接矩陣的函數。將鄰接矩陣中起始頂點 startPoint 和結束頂點 endPoint 所對應的位置的元素賦值為它們之間的絕對值差，即 abs(startPoint - endPoint)。這個值可以表示邊的權值或距離。由于是無向圖，所以將鄰接矩陣中結束頂點 endPoint 和起始頂點 startPoint 所對應的位置的元素也賦值為相同的絕對值差。將圖結構中的邊數 g->numEdges 加一，表示添加了一條新的邊。

void InputEdge(Graph* g, int n)：這段函數是用于輸入圖的邊并創建鄰接矩陣的函數聲明兩個整型變量 startPoint 和 endPoint，用于存儲輸入的邊的起始頂點和結束頂點。使用一個循環，循環次數為邊的數量 n。在每次循環中，通過輸入操作獲取用戶輸入的起始頂點和結束頂點，分別存儲到 startPoint 和 endPoint 變量中。調用 CreatMatrix 函數，將起始頂點和結束頂點作為參數傳遞給 CreatMatrix 函數，并將它們減去 1，以適應數組從 0 開始的索引。CreatMatrix 函數會根據傳入的起始頂點和結束頂點，在鄰接矩陣中設置相應的邊。

void OutputMatrix(Graph g,int n)：這段函數是用于輸出圖的鄰接矩陣的函數輸出一行提示信息，告訴用戶接下來要輸出圖的鄰接矩陣。使用兩個嵌套的循環，外層循環控制行數，內層循環控制列數，循環次數均為圖的頂點數量 n。在每次循環中，通過cout 語句輸出圖結構中鄰接矩陣的第 i 行第 j 列的元素，即 g.matrix[i][j]。在每行輸出完畢后，通過cout 語句輸出換行符 \n，使下一行的輸出從新的一行開始。

void DFSTravers(Graph &g,int i)：這段函數是用于實現深度優先搜索（DFS）遍歷圖的函數。

首先判斷頂點表中下標為 i 的頂點是否已經被遍歷，通過檢查 g.vex[i] 的值是否為 1 來判斷。如果頂點未被遍歷，則將 g.vex[i] 的值賦為 0，表示該頂點已被遍歷。使用一個循環，循環次數為圖的頂點數量 g.numVertices。在每次循環中，判斷從頂點 i 到頂點 j 是否存在邊，通過檢查 g.matrix[i][j] 的值是否大于 0 來判斷。如果存在邊，則遞歸調用 DFSTravers 函數，以頂點 j 作為新的起始頂點，繼續深度優先搜索遍歷。在遍歷完所有與頂點 i 相鄰的頂點后，通過 cout 語句輸出頂點 i 的值加 1，表示遍歷到了頂點 i。由于 DFS 是遞歸的過程，所以在遍歷完當前頂點后，會回溯到上一個頂點，繼續遍歷下一個未被遍歷的相鄰頂點。

void BFSTraverse(Graph &g)：這段函數是用于實現廣度優先搜索（BFS）遍歷圖的函數。

聲明一個數組 a 用于模擬隊列，初始化為全零。

聲明兩個計數器變量 countA 和 count，分別用于記錄遍歷次數和隊列的索引。

聲明一個標志變量 flag，用于判斷某個頂點是否已經出現過。

使用一個外層循環，循環條件為 countA < g.numVertices-1，即直到遍歷完所有頂點。

在每次循環中，使用一個內層循環，循環次數為圖的頂點數量 g.numVertices。

在內層循環中，首先判斷從隊列中當前索引位置 a[count] 到頂點 j 是否存在邊，通過 g.matrix[a[count]][j] 的值是否大于 0 來判斷。

如果存在邊，則使用一個額外的循環遍歷隊列 a，判斷頂點 j 是否已經在隊列中出現過。

如果頂點 j 之前未出現過，則將其添加到隊列中，即 a[++countA] = j。

在遍歷完當前頂點的所有相鄰頂點后，將 count 自增，繼續下一輪循環。循環結束后，使用一個循環輸出隊列 a 中的頂點，表示廣度優先搜索的遍歷順序。

void primMST(Graph* graph)：這個函數用于實現 Prim 算法求解最小生成樹的函數

首先聲明并初始化一些輔助數組和變量，包括 selected 數組用于標記頂點是否被選擇，parent 數組用于記錄頂點的父節點，minWeight 數組用于記錄頂點到最小生成樹的邊的權重，totalWeight 變量用于記錄最小生成樹的總權重。

然后初始化 minWeight 數組，將所有頂點的初始權重設為無窮大（INT_MAX），表示初始狀態下都不與最小生成樹相連。

接著將起始頂點的權重設為 0，表示該頂點為最小生成樹的起點。

然后使用一個循環，循環次數為圖的頂點數量減 1（因為最小生成樹有 n-1 條邊）。在每次循環中，找到權重最小的未選擇頂點（即 minWeight 數組中最小的值），記錄其索引為 minIndex。將該頂點標記為已選擇，并將其權重加到 totalWeight 中。遍歷所有未選擇的頂點，如果存在一條邊連接到該頂點且權重小于該頂點的當前最小權重，則更新該頂點的父節點為 minIndex，并更新其最小權重為邊的權重。

循環結束后，輸出最小生成樹的邊和總權重。

二源程序代碼

#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
#include <iostream>using namespace std;
/*對無向圖進行鄰接矩陣的轉化，并且利用DFS和BFS算法進行遍歷輸出，
在鄰接矩陣存儲結構上，完成最小生成樹的操作。*/
#define MAX_VERTICES 100
typedef struct Graph
{int vex[MAX_VERTICES] = { 0 };//頂點表 0為初始值，沒這個頂點int matrix[MAX_VERTICES][MAX_VERTICES];//鄰接矩陣int numVertices;//頂點數int numEdges;//邊數} Graph;
void initialMatrix(Graph *g,int n)//初始化矩陣，賦值為0
{for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){g->matrix[i][j] = 0;//數組從0開始}g->vex[i] = 1;//1代表有這個頂點}
}
void CreatMatrix(Graph *g,int startPoint,int endPoint)//創建鄰接矩陣
{g->matrix[startPoint][endPoint] = abs(startPoint-endPoint);g->matrix[endPoint][startPoint] = abs(startPoint-endPoint);//權值g->numEdges++;
}
void InputEdge(Graph* g, int n)//輸入相應邊
{int startPoint, endPoint;for (int i = 0; i < n; i++){cin >> startPoint;cin >> endPoint;CreatMatrix(g, startPoint-1, endPoint-1);}}void OutputMatrix(Graph g,int n)//輸出鄰接矩陣
{cout << "以下是圖的鄰接矩陣" << endl;for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){cout << g.matrix[i][j]<<" ";}cout << "\n";}
}void DFSTravers(Graph &g,int i)//從下標為0的點開始遍歷
{//先從第一個點開始遍歷，向任意一個方向進行遍歷//遍歷一個節點后將頂點表賦值為已遍歷//如果遍歷后的頂點無后續未遍歷的頂點則輸出，然后退回到上一個節點//由上一個節點的另外一個下一個節點開始遍歷依次遞歸if (g.vex[i] == 1)//說明此點未被遍歷{g.vex[i] = 0;for (int j = 0; j < g.numVertices; j++)//從0結點向后遍歷{if (g.matrix[i][j] >0){DFSTravers(g, j);}}cout << i+1<< " ";}
}
void BFSTraverse(Graph &g)
{//從第一個節點往下，一層一層遍歷，從左往右//一個節點遍歷之后，立刻輸出置為已訪問//剩下的節點再遍歷到之前的節點時就已訪問，然后不影響操作路徑int a[MAX_VERTICES] = { 0 };//數組模擬隊列int countA = 0; int count = 0;int flag = 0;for (int i=a[count]; countA < g.numVertices-1;i=a[count] )//countA代表循環次數{for (int j = 0; j < g.numVertices; j++){if (g.matrix[a[count]][j] >0){for (int k = 0; k < g.numVertices; k++){if (a[k] == j){flag = 1;//代表之前已出現過這個點flag = 2;break;}}if (flag == 0){a[++countA] = j;}if (flag == 2)flag = 0;}}count++;}for (int i = 0; i < g.numVertices; i++)cout << a[i] +1<< " ";}void primMST(Graph* graph) {int selected[MAX_VERTICES];int parent[MAX_VERTICES];int minWeight[MAX_VERTICES];int totalWeight = 0;for (int i = 0; i < graph->numVertices; i++) {selected[i] = 0;parent[i] = -1;minWeight[i] = INT_MAX;}minWeight[0] = 1;for (int count = 0; count < graph->numVertices - 1; count++) {int minIndex = -1;int min = INT_MAX;for (int i = 0; i < graph->numVertices; i++) {if (!selected[i] && minWeight[i] < min) {min = minWeight[i];minIndex = i;}}selected[minIndex] = 1;totalWeight += min;for (int i = 0; i < graph->numVertices; i++) {if (graph->matrix[minIndex][i] && !selected[i] && graph->matrix[minIndex][i] < minWeight[i]) {parent[i] = minIndex;minWeight[i] = graph->matrix[minIndex][i];}}}printf("\n最小生成樹邊緣：\n");for (int i = 1; i < graph->numVertices; i++) {printf("%d - %d\n", parent[i]+1, i+1);}printf("總重量： %d\n", totalWeight);
}int main()
{Graph g;int n;cout << "請輸入圖中的頂點個數" << endl;cin >> n;g.numVertices = n;initialMatrix(&g,n);cout << "請輸入邊的條數和組成邊的頂點" << endl;int numEdges;cin >> numEdges;InputEdge(&g,numEdges);OutputMatrix(g, n);cout << "深度優先搜索遍歷的結果為：" << endl;DFSTravers(g, 0);cout << "\n廣度優先搜索遍歷的結果為：" << endl;BFSTraverse(g);primMST(&g);return 0;
}

三、截圖

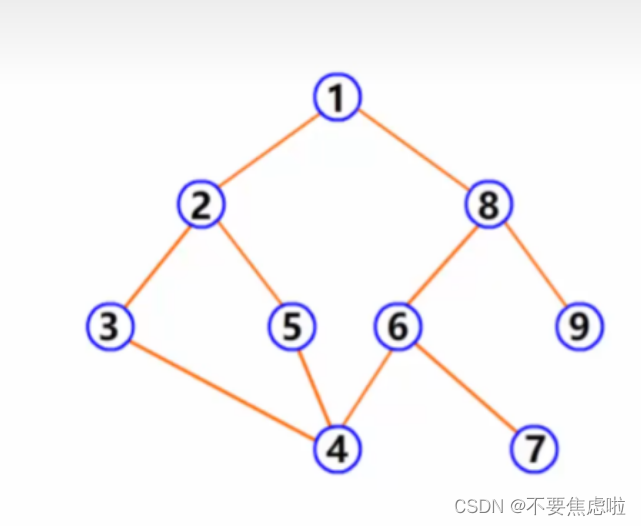
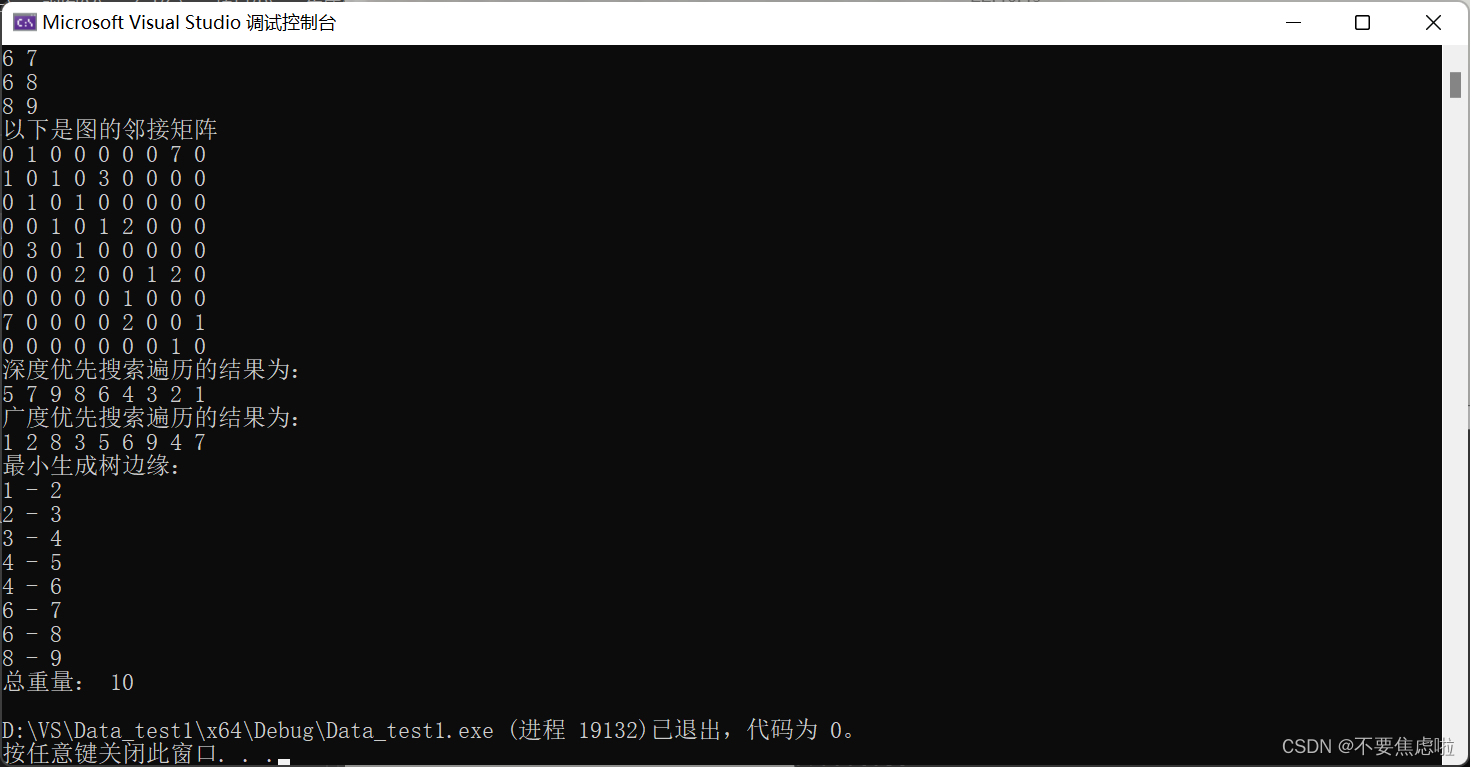
四調試情況、設計技巧及體會

本次實驗涉及到了建立無向圖的鄰接矩陣表示、深度優先搜索和廣度優先搜索遍歷以及最小生成樹的操作。通過完成這些實驗內容，我積累了一些寶貴的經驗和技巧，并且也遇到了一些典型的錯誤。以下是我對實驗過程中的錯誤及修改方法的總結，以及我從本次實驗中學到的技巧和經驗。

實驗過程中出現的典型錯誤及修改方法：

（1）鄰接矩陣的初始化有誤，導致后續操作出現問題

解決方法：對鄰接矩陣的初始化進行仔細檢查，確保每個元素都被正確地初始化。

（2）錯誤：在深度優先搜索或廣度優先搜索遍歷時，循環條件或循環變量設置錯誤。

修改方法：仔細檢查循環條件和循環變量的設置，確保循環能夠正確遍歷圖的所有頂點。注意邊界條件和循環變量的更新。

（3）錯誤：最小生成樹操作中，算法實現錯誤或遺漏了某些邊的處理。

修改方法：仔細閱讀最小生成樹算法的實現邏輯，確保每一步都按照算法的要求進行操作。特別是在選擇最小權重邊和更新頂點權重時，要仔細檢查條件和操作是否正確。

2. 學到的技巧和積累的經驗。

（1）在鄰接矩陣的創建過程中，我最初沒有正確理解鄰接矩陣的特性，導致了矩陣的構建錯誤。具體來說，我在構建鄰接矩陣時，沒有正確地處理頂點之間的雙向連接關系。在修正后，我明白了在鄰接矩陣中，如果頂點i與頂點j之間存在一條邊，那么矩陣的第i行和第j列上的元素值應為1，而其他位置的元素值應為0。

（2）在進行深度優先搜索時，我首先需要理解了它的基本原理：從圖的某個起始頂點開始，沿著一條路徑一直到達最深的頂點，然后回溯到之前的節點，繼續探索下一條路徑。在這個過程中，我犯了一個錯誤，那就是在訪問了某個頂點后沒有正確地回溯。修正這個錯誤后，我明白了在進行深度優先搜索時，必須正確處理訪問和未訪問的頂點狀態，才能確保遍歷的正確性。

在實現廣度優先搜索時，我遇到的問題是如何正確地訪問每一層的頂點。修正的方法是明白在廣度優先搜索中，需要使用一個隊列來存儲每一層的頂點，并且需要正確處理隊列的入隊和出隊操作。

（3）在進行Prim算法實驗時，我遇到的主要問題是如何正確地找到最小邊以及如何正確地將新頂點加入生成樹中。修正的方法是理解并實現了一個優先隊列來存儲邊，并按照邊的權重進行排序。同時，我也學會了如何正確地更新生成樹中的頂點和邊。