一? 需求解函數

f() 和 g()函數分別為求y值和求導數的函數。

目的：求該函數的最小值：

????????

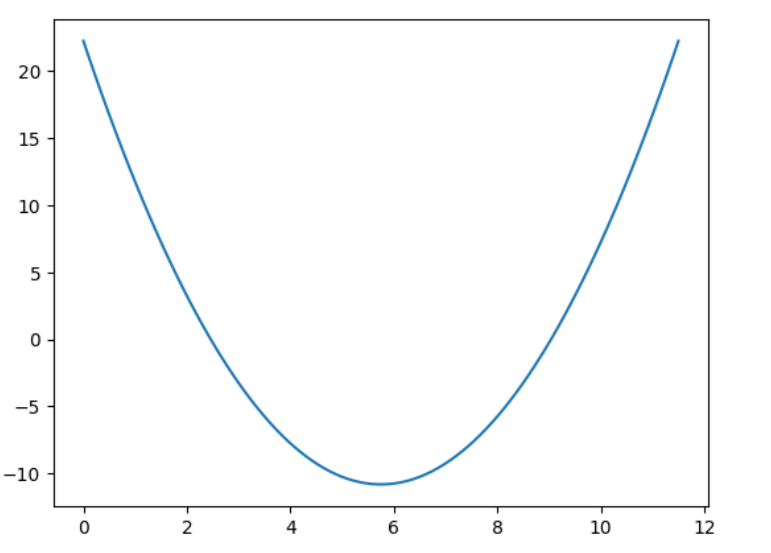
?代碼：

import numpy as np
import matplotlib.pyplot as plt f = lambda x : (x - 3.5) ** 2 - 4.5 * x + 10
g = lambda x : 2 * (x - 3.5) - 4.5x = np.linspace(0, 11.5, 100)
y = f(x)plt.plot(x, y) 

二 隨機初始化一個值

在 0 - 12 中隨機取一個值：10

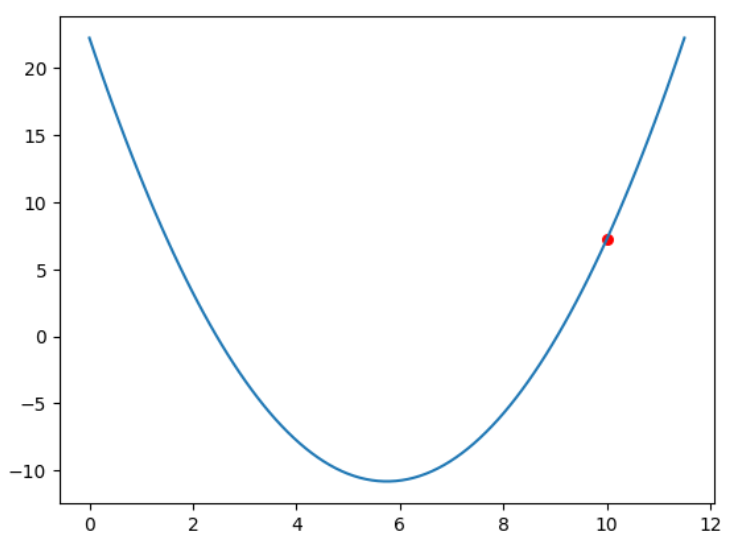
k = np.random.randint(0, 12)
print('隨機取到的值k:', k)  # 10 

三 查看此時的斜率

查看此時的切線方程：

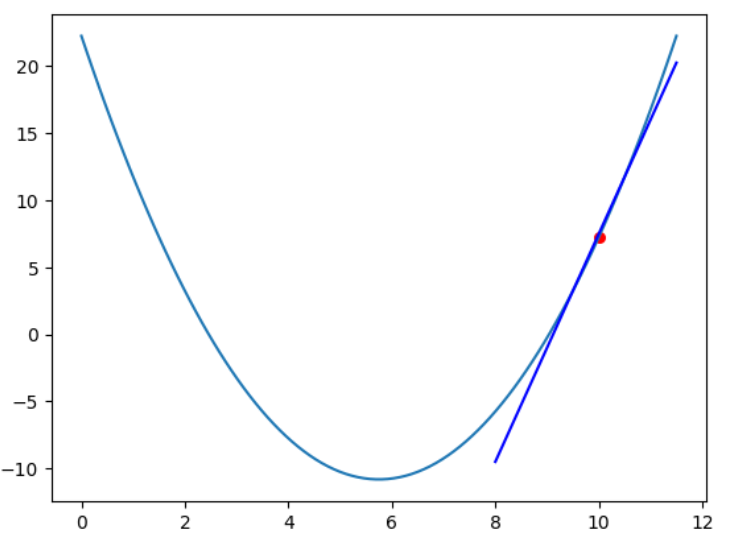
k = 10
g(x) = 8.5   # 斜率
f(x) = 7.5   # y值
# 該點的切線方程：y = 8.5 * x - 77.5plt.plot(x, y) 
plt.scatter(k, f(k), color = 'red', s = 30)# 生成x的范圍
x_values = np.linspace(8, 11.5, 100)# 計算對應的y值
y_values = 8.5 * x_values - 77.5
# 繪制直線
plt.plot(x_values, y_values, color='blue', label='Line')

四 根據斜率和學習率確定下一個點

設置學習率為0.2，與初始點的梯度反向進行下降，如果在上一個點斜率為正，說明需要x需要向左移動才能接近最小值：next_k = k - 學習率*斜率

學習率可以改，設置值比較大移動比較快，設置比較小移動比較慢。

求到的第一個K：8.3

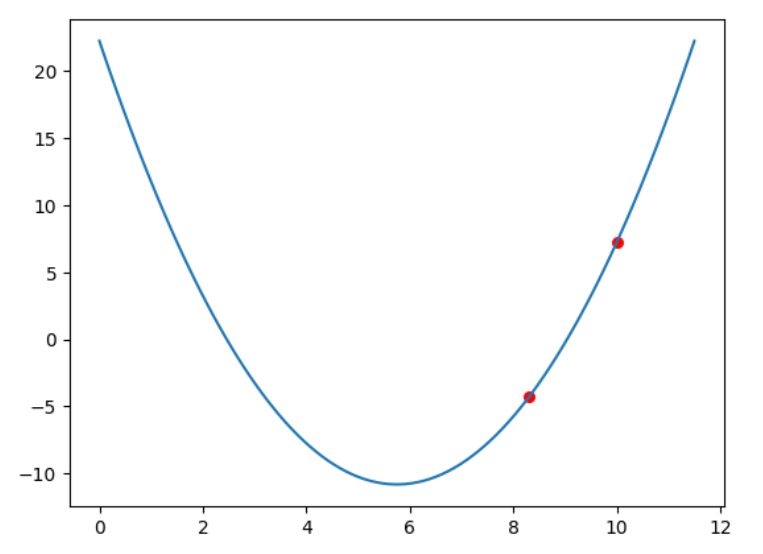
learing_ratio = 0.2
next_k = k - learing_ratio*g(k) plt.plot(x, y) 
plt.scatter(k, f(k), color = 'red', s = 30)
plt.scatter(next_k, f(next_k), color = 'red', s = 30) print(next_k, f(next_k))
# 8.3 -4.309999999999995

五?根據該邏輯繼續計算下一個值

用上一次計算的 8.2 計算一個值：next_k2 = next_k - learing_ratio*g(next_k)?。

求到的第二個K：7.28

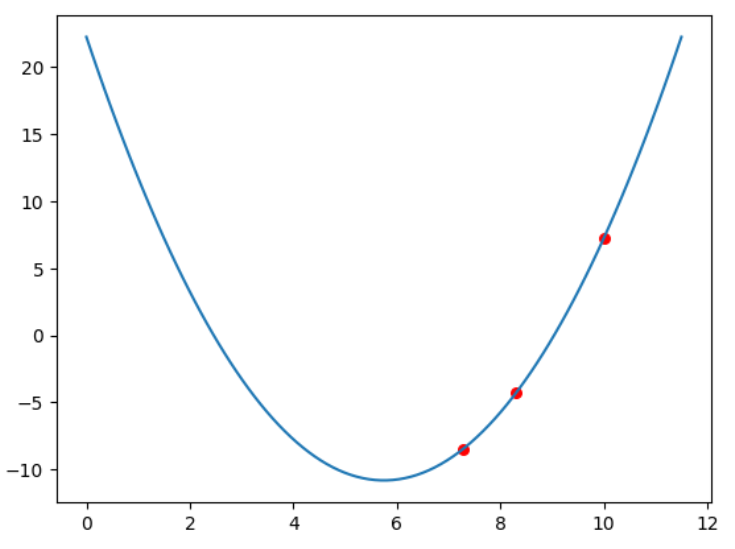
learing_ratio = 0.2
next_k2 = next_k - learing_ratio*g(next_k) plt.plot(x, y) 
plt.scatter(k, f(k), color = 'red', s = 30)
plt.scatter(next_k, f(next_k), color = 'red', s = 30)
plt.scatter(next_k2, f(next_k2), color = 'red', s = 30)
print(next_k2, f(next_k2))
# 7.28 -8.471599999999995

六 同時查看兩次迭代過程中 y值的變化率

查看兩次迭代過程中 y值的變化率分別為：-11.559999999999995? -4.1616

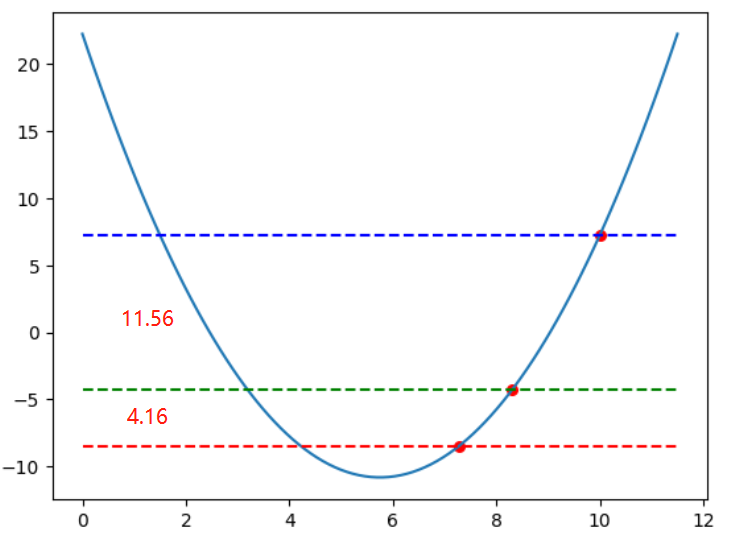
plt.plot(x, y) 
plt.scatter([k, next_k, next_k2], [f(k), f(next_k), f(next_k2)], color = 'red', s = 30)# 繪制直線
plt.plot(x, [f(k)] * len(x), label='y=5', color='blue', linestyle='--')
plt.plot(x, [f(next_k)] * len(x), label='y=5', color='green', linestyle='--')
plt.plot(x, [f(next_k2)] * len(x), label='y=5', color='red', linestyle='--')print(f(next_k) - f(k), f(next_k2) - f(next_k))  # -11.5599999999-4.1616

七 設置循環，求最接近的目標值

注意：截止條件設置的變化率是x 的變化率，就是當?斜率的變化值足夠小?的時候截止，其實也是y值的變化率乘學習率后的變化值 ！！

k = k - learing_ratio*g(k)

設置截止循環條件：precision = 0.0001

learing_ratio = 0.2
last_k = k + 0.1
# 精確度
precision = 0.0001k_ = [k]
count = 0  # 記錄迭代次數while True:if np.abs(k - last_k) < precision:breaklast_k = kcount += 1k = k - learing_ratio*g(k)  # 迭代k_.append(k)print(f'-> 迭代次數cnt:{count:2},更新后的x:{k:0.7f}, 實時的y:{f(k):0.7f}')print(f'梯度下降的次數：{count}')
plt.plot(x, y) 
print('最后的k值：', k)  # 5.75009323204022# 散點圖，轉換為array數組可以用f(x)直接求列表的y值
k_ = np.array(k_)
plt.scatter(k_, f(k_), color = 'red', s = 30)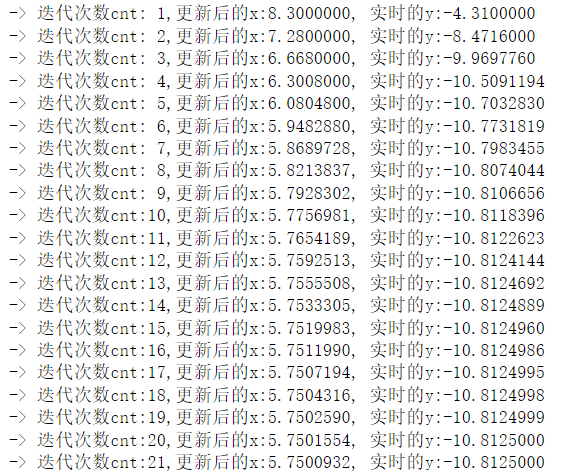

?

PS：最后的列表直接求y值是先轉換為了 np.array數組！！！

實際值：5.75

循環21次，最后求到的k值：5.75009323204022