$2^n$

1<<n

判斷某一位是否為1

s&1<<k

將上面兩個組合，可以得到判斷一個集合中哪些內容包含，遍歷所有情況。

100140. 關閉分部的可行集合數目

一個公司在全國有 n 個分部，它們之間有的有道路連接。一開始，所有分部通過這些道路兩兩之間互相可以到達。

公司意識到在分部之間旅行花費了太多時間，所以它們決定關閉一些分部（也可能不關閉任何分部），同時保證剩下的分部之間兩兩互相可以到達且最遠距離不超過 maxDistance 。

兩個分部之間的 距離 是通過道路長度之和的 最小值 。

給你整數 n ，maxDistance 和下標從 0 開始的二維整數數組 roads ，其中 roads[i] = [ui, vi, wi] 表示一條從 ui 到 vi 長度為 wi的 無向 道路。

請你返回關閉分部的可行方案數目，滿足每個方案里剩余分部之間的最遠距離不超過 maxDistance。

注意，關閉一個分部后，與之相連的所有道路不可通行。

注意，兩個分部之間可能會有多條道路。
示例 1：

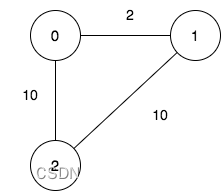
輸入：n = 3, maxDistance = 5, roads = [[0,1,2],[1,2,10],[0,2,10]]
輸出：5
解釋：可行的關閉分部方案有：

• 關閉分部集合 [2] ，剩余分部為 [0,1] ，它們之間的距離為 2 。
• 關閉分部集合 [0,1] ，剩余分部為 [2] 。
• 關閉分部集合 [1,2] ，剩余分部為 [0] 。
• 關閉分部集合 [0,2] ，剩余分部為 [1] 。
• 關閉分部集合 [0,1,2] ，關閉后沒有剩余分部。
  總共有 5 種可行的關閉方案。
  示例 2：
  
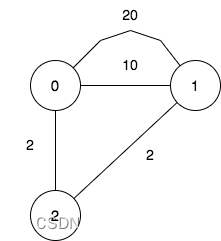
  輸入：n = 3, maxDistance = 5, roads = [[0,1,20],[0,1,10],[1,2,2],[0,2,2]]
  輸出：7
  解釋：可行的關閉分部方案有：
• 關閉分部集合 [] ，剩余分部為 [0,1,2] ，它們之間的最遠距離為 4 。
• 關閉分部集合 [0] ，剩余分部為 [1,2] ，它們之間的距離為 2 。
• 關閉分部集合 [1] ，剩余分部為 [0,2] ，它們之間的距離為 2 。
• 關閉分部集合 [0,1] ，剩余分部為 [2] 。
• 關閉分部集合 [1,2] ，剩余分部為 [0] 。
• 關閉分部集合 [0,2] ，剩余分部為 [1] 。
• 關閉分部集合 [0,1,2] ，關閉后沒有剩余分部。
  總共有 7 種可行的關閉方案。
  示例 3：

輸入：n = 1, maxDistance = 10, roads = []
輸出：2
解釋：可行的關閉分部方案有：

• 關閉分部集合 [] ，剩余分部為 [0] 。
• 關閉分部集合 [0] ，關閉后沒有剩余分部。
  總共有 2 種可行的關閉方案。

class Solution {
public:int e[20][20];int dis[20][20];int numberOfSets(int n, int lim, vector<vector<int>>& roads) {int rt=0;memset(e,0x3f,sizeof(e));for(auto &p:roads){int u=p[0],v=p[1],w=p[2];e[v][u]=e[u][v]=min(e[u][v],w);}for(int i=0;i<n;i++) e[i][i]=0;for(int s=0;s<1<<n;s++){memcpy(dis,e,sizeof(dis));for(int k=0;k<n;k++) if(s&1<<k)for(int i=0;i<n;i++) if(s&1<<i)for(int j=0;j<n;j++) if(s&1<<j)dis[i][j]=min(dis[i][k]+dis[k][j],dis[i][j]);for(int i=0;i<n;i++) if(s&1<<i)for(int j=0;j<n;j++) if(s&1<<j)if(dis[i][j]>lim) goto fail;//cout<<"suc "<<s<<endl;rt++;fail:;}return rt;}
};