目錄

歸并排序

歸并排序的時間復雜度

?排序的穩定性

排序總結

---

歸并排序

歸并排序大家只需要掌握其遞歸方法即可，非遞歸方法由于在某些特殊場景下邊界難控制，我們一般很少使用非遞歸實現歸并排序。那么歸并排序的遞歸方法我們究竟是怎樣實現呢？

大家先想象一下這樣一種場景，如果現在有兩個數，我們要將這兩個數排成升序，怎樣呢？很簡單，我們只需要將兩個數進行一次大小的比較即可，比較完之后，小的元素放在前面，大的元素放在后面，其實這就是很簡單的一次歸并排序，兩個素比較之后交換使得兩個元素變得有序的場景我們就稱作一次歸并。

? ? ? ? 我們再次深入分析，如果有兩個元素，這兩個元素可以直接比較，且比較之后兩個數就變得有序，以此類推，如果們要對4個元素進行歸并排序，按照此邏輯，將兩兩分成一組，然后這兩組進行一次比較，比較完成之后，這4個元素應該就變有序了，但是事實真是這樣嗎？通過示意圖為大家講解：

?為什么兩個元素互相比較就可以變得有序呢？

?這是因為當一個數組中只有一個數時，我們就可以稱這個數組是有序的，當數組中有兩個元素時，我們可以將這兩個數每一個數都看成一個數組，此時這兩個數組都是有序的，兩個有序的數組，元素之間依次比較，肯定會將最終的整個數組變得有序，所以，我們要使四個數組變得有序，可以將數組分成左右兩個數組，當我們使左右兩個數組有序時，再將左右兩個數組的元素依次進行比較，這樣，最終四個數組成的數組就會有序。以此，歸并排序的遞歸思路就出來了：

通過四個元素的數組為大家圖示講解歸并排序的思想：?

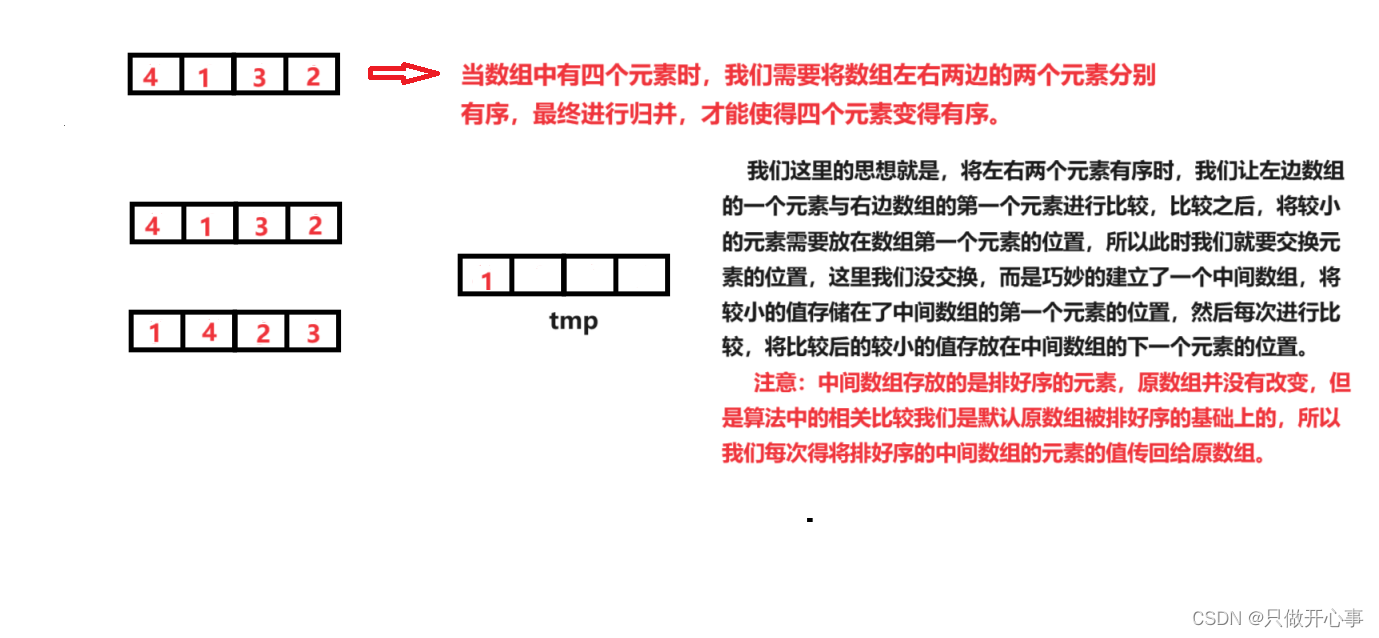
歸并排序的思想：我們要對一個數組進行歸并排序，使它變得有序，我們就得先將這個數組分成左右兩部分，相對左邊這部分數組進行歸并排序，然后再對右邊這部分數組進行歸并排序，左右兩邊的數組排好序之后，對左右兩個數組的元素進行一次比較，我們也成對左右兩個數組的元素進行歸并，然后整個數組的歸并排序就完成了。

歸并排序的整體代碼：

void _MergeSort(int* a, int left, int right, int* tmp)
{if (left >= right)return;int mid = (right + left) / 2;_MergeSort(a, left, mid, tmp);_MergeSort(a, mid + 1, right, tmp);int begin1 = left, begin2 = mid + 1;int end1 = mid, end2 = right;int i = left;//左右數組有序之后，就需要左右數組進行歸并while (begin1 <= end1 && begin2 <= end2){if (a[begin1] < a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}//左右兩個數組，當一個數組歸并完時，一個數組可能還沒有歸并完，將沒有歸并完的這個數組的元素依次賦值給中間數組while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin1 <= end1){tmp[i++] = a[begin2++];}for (int j = 0; j < right + 1; j++){a[j] = tmp[j];}
}
void MergeSort(int* a, int size)
{int* tmp = (int*)malloc(sizeof(int) * size);if (tmp == NULL){printf("malloc fail");exit(-1);}_MergeSort(a, 0, size - 1, tmp);free(tmp);tmp = NULL;
}
int main()
{int arr[] = {99,88,66,77,55,44,33,22,11 };MergeSort(arr,sizeof(arr)/sizeof(int));for (int i = 0; i < sizeof(arr) / sizeof(int); i++){printf("%d ", arr[i]);}return 0;
}

運行截圖：

????????

歸并排序的時間復雜度

時間復雜度：O(N*logN)? ? ?

穩定性:穩定

?排序的穩定性

什么是排序的穩定性呢？

其實就是，在未排序之前，數組中有兩個相同的元素（有順序），如果在排序之后這兩個元素的順序沒有發生變化，則稱這個排序是穩定的，如果排序之后順序發生了變化，我們就稱這個排序算法是不穩定的。

排序總結

? ? ? ? ? 直接插入排序：最好的情況下就是一個有序數組，插入的元素只用跟前面數組的最后一個元素比較，最好復雜度為O(N)。最壞的情況就是一個逆序數組，每個要插入的元素都要和前面的數組元素比較一下，就是等差數列求和O(N^2)
? ? ? ? ? 希爾排序：時間復雜度不好計算，大概是O(N^1.3)
? ? ? ? ? 選擇排序：沒有最好和最壞，編譯器不知道所以，每個元素都和最小的元素比較一次，一趟排序確定了一元素的位置，剩下的元素下一趟繼續進行比較，時間復雜度為等差數列求和O(N^2)
? ? ? ? ? 堆排序：沒有最好和最壞，因為都是從一個大堆或者小堆進行調整，為O(N*logN)
? ? ? ? ? 冒泡排序：有序時，我們有優化，一趟比較下來沒有發生交換，所以終止后面的排序，但是第一趟的相鄰兩個元素都發生了比較，比較了N次，所以最好時間復雜度為O(N),最壞，逆序，等差數列求和O(N^2)
? ? ? ? ?快速排序：最好：每次找到的key都在中間，所以剛好是一個滿二叉樹，高度為logN，每層比較N次，總共比較N*logN次，所以最好為O(N*logN)
? ? ? ? ? ? ? ? ? ? ? ? ? 最壞：一個有序數組，每次找的key都在最左邊，總共N層，比較等差數列求和次，所以最壞為O(N^2)
? ? ? ? ?歸并排序：最好最壞都是O(N*logN)

? ? ? ? 只有快速排序和歸并排序他們倆才會消耗額外額空間，因為遞歸要頻繁的消耗棧幀，且快排非遞歸實現時運用了棧的數據結構。

好了，到此常見的排序算法我們已經全部學寫完成了，排序算法是面試中的重點，大家一定要掌握。

好了，本期的內容到此結束^_^