排列組合

2023

真題（2023-05）-數據分析-排列組合-組合-C運算-至少-需反面思考

真題（2023-08）-數據分析-排列組合-相鄰+不相鄰-捆綁法+插空法-插空法注意空位比座位多1個，是用A；捆綁法內部排序用A；

2022

真題（2022-10）-算術-質數±數據分析-排列組合

10.一個自然數的各位數字都是 105 的質因數，且每個質因數最多出現一次，這樣的自然數有（ ）個。
A.6
B.9
C.12
D.15
E.27

真題（2022-12）-數據分析-排列組合-闖關題

12.甲乙兩支足球隊進行比賽，比分為 4:2，且在比賽過程中乙隊沒有領先過，則不同的進球順序有（ ）。
A.6 種
B. 8 種
C. 9 種
D. 10 種
E. 12 種

真題（2022-13）-數據分析-排列組合-排隊-相鄰不相鄰-不相鄰插空法

13.4 名男生和 2 名女生隨機站成一排，則女生既不在兩端也不相鄰的概率為（ ）
A.$\frac{1}{2}$
B.$\frac{5}{12}$
C.$\frac{3}{8}$
D.$\frac{1}{3}$
E.$\frac{1}{5}$

真題（2022-15）-數據分析-排列組合-涂色

15.如圖，用 4 種顏色對圖中五塊區域進行涂色，每塊區域涂一種顏色，且相鄰的兩塊區域顏色不同，不同的涂色方法有（ ）種
A.12
B.24
C.32
D.48
E.96


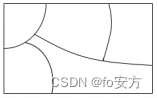
涂色
（1）直線涂色：簡單的乘法原理。
（2）環形涂色公式：把一個環形區域分為k塊，每塊之間首尾相連，用s種顏色去涂，要求相鄰兩塊顏色不同，則不同的涂色方法有
$N=(s—1{)}^k＋(s—1)(?1{)}^k$，式中，s為顏色數（記憶方法：se色），k為環形被分成的塊數（記憶方法：kuai 塊）。——【環形涂色公式：色減一的塊次冪】

2021

真題（2021-08）-數據分析-排列組合-計數原理-加法原理

8.甲.乙兩組同學中，甲組有3男3女，乙組有4男2女，從甲、乙兩組中各選出2名同學，這4人中恰有1女的選法有( )種。
A.26
B.54
C.70
D.78
E.105

2020

真題（2020-15）-數據分析-排列組合-不同元素的分配問題

15、某科室有 4 名男職員，2 名女職員，若將這 6 名職員分為 3 組，每組兩人，且女職員不同組，則分法有（ ）種
A.4
B.6
C.9
D.12
E.15

2019

真題（2019-14）-數據分析-排列組合-組合-C運算

14、某中學的 5 個學科各推薦 2 名教師作為支教候選人，若從中選出來自不同學科的 2 人參加支教工作，則不同的選派方式有( )種。
A. 20
B. 24
C. 30
D. 40
E. 45

2018

2017

2016

2015

2014

2013

概率

2023

真題（2023-25）-數據分析-概率-已知事件的概率求概率? 獨立事件概型? 乘法計算概率

2022

真題（2022-05）-數據分析-概率-已知元素的數量求概率? 古典概型? 兩個排列組合相除計算概率或窮舉法? 分母是C運算，分子數量少用窮舉，數量多用C運算

5.如圖，已知相鄰的圓都相切，從這 6 個圓中隨機取 2 個，這 2 個圓不相切的概率為（ ）
A.$\frac{8}{15}$
B.$\frac{7}{15}$
C.$\frac{3}{5}$
D.$\frac{2}{5}$
E.$\frac{2}{3}$

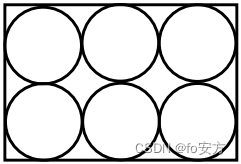
2021

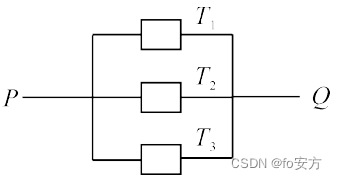
真題（2021-06）-數據分析-概率已知事件的概率求概率? 獨立事件概型? 乘法計算概率

6.如圖，由P到Q電路中有三個元件，分別為$T_1,T_2,T_3$，電流能通過$T_1,T_2,T_3$概率分別為0.9，0.9，0.99，假設電流能否通過三個元件相互獨立，則電流能在P、Q之間通過的概率是( )。
A.0.8019
B.0.9989
C.0.999
D.0.9999
E.0.99999

真題（2021-11）-數據分析-概率-已知元素的數量求概率? 古典概型? 兩個排列組合相除計算概率或窮舉法? 分母有順序要求是A運算，無順序是C運算，分子數量少用窮舉，數量多用C運算? 袋中取球模型？？

11.某商場利用抽獎方式促銷，100個獎券中設有3個一等獎，7個二等獎，則一等獎先于二等獎抽完的概率為( )
A.0.3
B.0.5
C.0.6
D.0.7
E.0.73

真題（2021-14）-數據分析-概率-已知元素的數量求概率? 古典概型? 兩個排列組合相除計算概率或窮舉法? 分母有順序要求是A運算，無順序是C運算，分子數量少用窮舉，數量多用C運算? 袋中取球模型? 正難則反? 轉為一次取球模型? 設口袋中有a個白球，b個黑球，一次取出若干個球，則恰好取了$m(m\le a)$個白球，$n(n\le b)$個黑球的概率是$P=\frac{C_a^m?C_b^n}{C_{a+b}^{m+n}}$。

14.從裝有1個紅球，2個白球，3個黑球的袋中隨機取出3個球，則這3個球的顏色至多有兩種的概率（ ）
A.0.3
B.0.4
C.0.5
D.0.6
E.0.7

2020

真題（2020-04）-數據分析-概率-已知元素的數量求概率? 古典概型? 兩個排列組合相除計算概率或窮舉法? 分母有順序要求是A運算，無順序是C運算，分子數量少用窮舉，數量多用C運算；-算術-質數-2,3,5,7,11,13,17,19,23,29；

4、從 1 至 10 這 10 個整數中任取 3 個數，恰有 1 個質數的概率是（ ）
A. $\frac{2}{3}$
B. $\frac{1}{2}$
C. $\frac{5}{12}$
D. $\frac{2}{5}$
E.$\frac{1}{120}$

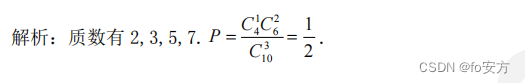
真題（2020-14）-數據分析-概率-已知事件的概率求概率? 獨立事件概型? 乘法計算概率

14.節點 A, B, C, D 兩兩相連，從一個節點沿線段到另一個節點當作 1 步，若機器人從節點 A出發，隨機走了 3 步，則機器人從未經過節點C 的概率為（ ）

A.$\frac{4}{9}$
B. $\frac{11}{27}$
C. $\frac{10}{27}$
D. $\frac{19}{27}$
E. $\frac{8}{27}$

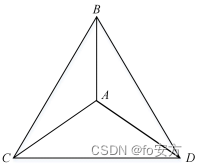
真題（2020-19）-數據分析-概率-已知元素的數量求概率? 古典概型? 兩個排列組合相除計算概率或窮舉法? 分母有順序要求是A運算，無順序是C運算，分子數量少用窮舉，數量多用C運算? 袋中取球模型? 正難則反? 轉為一次取球模型? 設口袋中有a個白球，b個黑球，一次取出若干個球，則恰好取了$m(m\le a)$個白球，$n(n\le b)$個黑球的概率是$P=\frac{C_a^m?C_b^n}{C_{a+b}^{m+n}}$。翻譯“≥≤”-準確率90%-D：題干或選項可以翻譯成≥或≤的，選D

19、甲、乙兩種品牌手機共有 20 部，從中任選 2 部，則恰有 1 部甲品牌手機的概率大于$\frac{1}{2}$。
（1）甲手機不少于 8 部
（2）乙手機大于 7 部

2019

真題（2019-07）-數據分析-概率-已知元素的數量求概率? 古典概型? 兩個排列組合相除計算概率或窮舉法? 分母是C運算，分子數量少用窮舉，數量多用C運算

7、在分別標記 1,2,3,4,5,6 的 6 張卡片，甲抽取一張，乙從余下的卡片中再抽取 2 張，乙的卡片數字之和大于甲的卡片數字的概率為（）
A.$\frac{11}{60}$
B.$\frac{13}{60}$
C.$\frac{43}{60}$
D.$\frac{47}{60}$
E.$\frac{49}{60}$

【解析】母題82·古典概型方法一：采用窮舉法.
當甲抽取卡片1時，乙有$C_5^2=10$(種)選法；
當甲抽取卡片2時，乙有$C_5^2=10$(種)選法；
當甲抽取卡片3時，乙有9種選法；
當甲抽取卡片4時，乙有8種選法；
當甲抽取卡片5時，乙有6種選法；
當甲抽取卡片6時，乙有4種選法。
以上合計47種選法。
總的事件數為$C_5^1{C}_5^2=60$(種)，故所求概率為$\frac{47}{60}$。
方法二：求對立事件
事件總數為$C_5^1{C}_5^2=60$(種).
如果甲抽取卡片6，則乙的卡片數字之和小于等于甲的情況有(5,1),(4,2),(4,1),(3,2),(3,1),(1,2),共6種；
如果甲抽取卡片5，則乙的卡片數字之和小于等于甲的情況有(4,1),(3,2),(3,1),(1,2),共4種；
如果甲抽取卡片4，則乙的卡片數字之和小于等于甲的情況有(3,1),(1,2),共2種；
如果甲抽取卡片3，則乙的卡片數字之和小于等于甲的情況有(1,2)，共1種。
故所求概率=$1?\frac{6+4+2+1}{60}=\frac{47}{60}$，故選(D).

真題（2019-17）-數據分析-概率已知事件的概率求概率? 獨立事件概型? 乘法計算概率

17、有甲乙兩袋獎券，獲獎率分別為 p 和q ，某人從兩袋中各隨機抽取 1 張獎券，則此人獲獎的概率不小于$\frac{3}{2}$
(1) 已經$p+q=1$
(2) 已知 $pq=\frac{1}{4}$

2018

2017

2016

2015

2014

2013

數據描述

2023

真題（2023-12）-數據分析-數據描述-快速比較方差的大小-極差大的，數據波動大，方差就大；極差小的，數據波動小，方差就小。

2022

2021

2020

真題（2020-03）-數據分析-數據描述-平均值

3、一項考試的總成績由甲乙丙三部分組成：總成績=甲成績×30% +乙成績×20% +丙成績×50% ，考試通過的標準是：每部分≥50 分，且總成績≥60 分。已知某人甲成績 70 分，乙成績 75 分，且通過了這項考試，則此人丙成績的分數至少是（ ）
A.48
B.50
C.55
D.60
E.62

真題（2020-09）-數據分析-數據描述-平均值與方差-分歧大不是方差大

9、某人在同一觀眾群中調查了對五部電影的看法，得到如下數據：

電影	第一部	第二部	第三部	第四部	第五部
好評率	0.25	0.5	0.3	0.8	0.4
差評率	0.75	0.5	0.7	0.2	0.6

據此數據，觀眾意見分歧較大的兩部影片依次是（ ）
A.一三
B.二三
C.二五
D.四一
E.四二

真題（2020-18）-數據分析-數據描述-平均值與方差

18、若a, b, c 是實數，則能確定a, b, c 的最大值。
（1）已知a, b, c 的平均值。
（2）已知a, b, c 的最小值。

2019

真題（2019-08）-數據分析-數據描述-方差

8、10 名同學的語文和數學成績如表

語文成績	90	92	94	88	86	95	87	89	91	93
數學成績	94	88	96	93	90	85	84	80	82	98

語文和數學成績的均值分別為 $E_1$ 和 $E_2$ ，標準差分別為${\sigma }_1$和 ${\sigma }_2$，則
A.$E_1＞E_2，{\sigma }_1＞{\sigma }_2$
B.$E_1＞E_2，{\sigma }_1＜{\sigma }_2$
C.$E_1＞E_2，{\sigma }_1={\sigma }_2$
D.$E_1＜E_2，{\sigma }_1＞{\sigma }_2$
E.$E_1＜E_2，{\sigma }_1＜{\sigma }_2$

【解析】母題99·圖像圖表問題＋母題18·平均值與方差
$E_1=\frac{90+92+94+88+86+95+87+89+91+93}{10}=90.5$
$E_2=\frac{94＋88＋96＋93+90+85+84+80+82+98}{10}=89$
顯然$E_1＞E_2$，通過觀察可知語文成績的離散程度小于數學成績，故有${\sigma }_1＜{\sigma }_2$。或者通過計算方差也可得出答案。

真題（2019-23）-數據分析-數據描述-平均值

23、某校理學院五個系每年錄取人數如下表：

系數	數學系	物理系	化學系	生物系	地學系
錄取人數	60	120	90	60	30

今年與去年相比，物理系平均分沒交，則理學院錄取平均分升高了。
(1) 數學系錄取平均分升高了 3 分，生物系錄取平均分降低了 2 分
(2) 化學系錄取平均分升高了 1 分，地學系錄取平均分降低了 4 分

2018

2017

2016

2015

2014

2013