要學習scikit-learn,我們必須要到scikit-clearn的官網中去查看公式和原理
scikit-learn 官網
scikit-learn 中文社區
進入官網一以后我們找到回歸，然后再有監督學習中找到線性模型

scikit-learn實現簡單的線性回歸

公式：

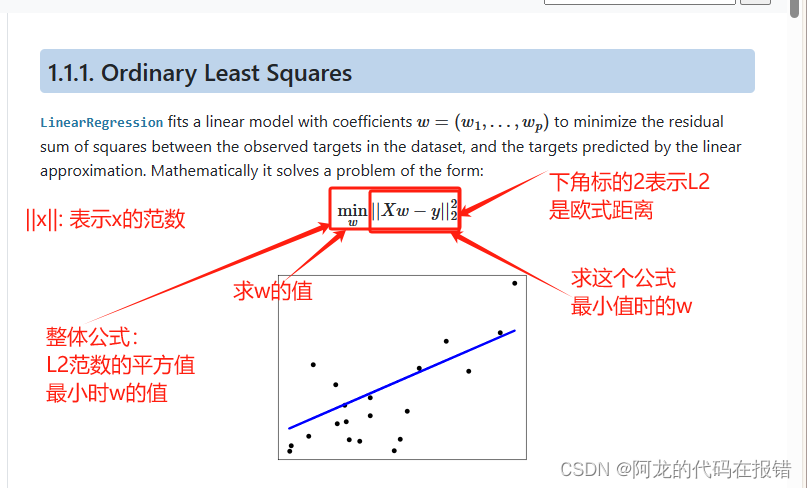
L2范數是指向量中每個元素的平方和的平方根。在數學中，L2范數也稱為歐幾里得范數，通常用 $||x|{|}_2$ 表示，其中x是一個向量。L2范數可用于衡量向量的大小或長度。

L2范數在機器學習和數據科學中經常用于正則化和優化問題中，例如嶺回歸和支持向量機等算法。在這些情況下，通過對損失函數添加L2正則化項，可以避免過擬合并提高模型的泛化能力。同時，L2范數也被用來作為相似性度量的度量標準，如余弦相似性。

L2范數公式：
$||x|{|}_2=\sqrt{(\sum |x_i{|}^2)}$

代碼實現 ：

import numpy as np 
import matplotlib.pyplot as plt 

模擬數據

X = np.linspace(0, 10, num=30).reshape(-1, 1)
# 斜率和截距，隨機生成
w = np.random.randint(1, 5, size=1)
b = np.random.randint(1, 10, size=1)
# 根據一元一次方程計算目標值y并加上‘噪聲’，數據有上下波動
y = X * w + b +np.random.randn(30,1)  # 注意要添加噪聲避免出現過擬合
plt.scatter(X,y)  # 將圖形展現出來

計算斜率和截距

from sklearn.linear_model import LinearRegression
# 創建對象 
model = LinearRegression(fit_intercept=True) # fit_intercept ：是否計算裁距
model.fit(X,y)
print("算法求得的系數,斜率",model.coef_)
print('算法求得的截距',model.intercept_)

和算法求得的斜率和截距進行對比驗證

print("這是真實的斜率和截距是",w,b)

獲取擬合后的圖形

plt.scatter(X,y,color='red')
plt.plot(X,model.coef_*X +model.intercept_,color='green')

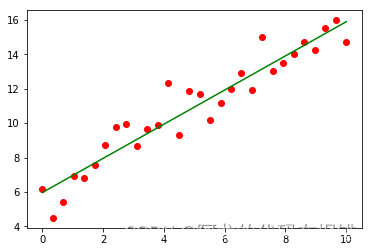
這個時候我們要哦特別注意的是：
model = LinearRegression(fit_intercept=False) # fit_intercept
在使用 LinearRegression創建對象的時候，fit_intercept參數開啟則計算裁距
如果不計算裁距情況，如何獲得集合的圖形

from sklearn.linear_model import LinearRegression
# 創建對象 
model = LinearRegression(fit_intercept=False) # fit_intercept ：是否計算裁距
X_ = np.concatenate([X,np.full(shape=(30,1),fill_value=1)],axis=1)
model.fit(X_,y)
print("算法求得的系數,斜率",model.coef_)
print('算法求得的截距',model.intercept_)

plt.scatter(X,y,color='red')
plt.plot(X,model.coef_[0,0]* X +model.coef_[0,1],color='green')

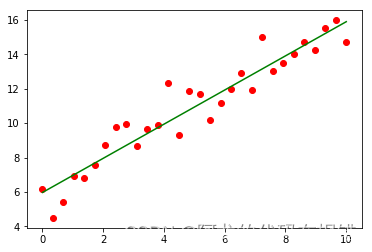
獲取系數

np.linalg.inv(X_.T.dot(X_)).dot(X_.T).dot(y)

scikit-learn實現多元的線性回歸

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.axes3d import Axes3D  # 繪制三維圖像

模擬數據

# 轉化為矩陣
x1 = np.random.randint(-150, 150, size=(300, 1))
x2 = np.random.randint(0, 300, size=(300, 1))
# 斜率和截距，都是隨機生成的
w = np.random.randint(1, 5, size=2)
b = np.random.randint(1, 10, size=1)
# 根據二元一次方程計算目標值y 并且加上“噪聲”，讓數據上下波動
y = x1 * w[0] + x2 * w[1] + b + np.random.randn(300, 1)

創建對象

from sklearn.linear_model import LinearRegression
model = LinearRegression()
X = np.concatenate([x1,x2],axis = 1)
model.fit(X,y)
print(model.coef_,model.intercept_)

輸出真實的斜率和系數用于與算法得出的數值進行對比

print(w,b)

生成擬合圖形

# 特征1：x1
x_axis = np.linspace(-150,150,num=500)
# 特征2 ：x2 
y_axis = np.linspace(0,300,num=500)
# 方程 斜率，截距
Z_axis = x_axis * model.coef_[0,0] +y_axis * model.coef_[0,1]+ model.intercept_
fig = plt.figure(figsize=(9,6))
ax = Axes3D(fig)
ax.scatter(x1,x2,y) #三維散點圖
ax.plot(x_axis,y_axis,Z_axis)

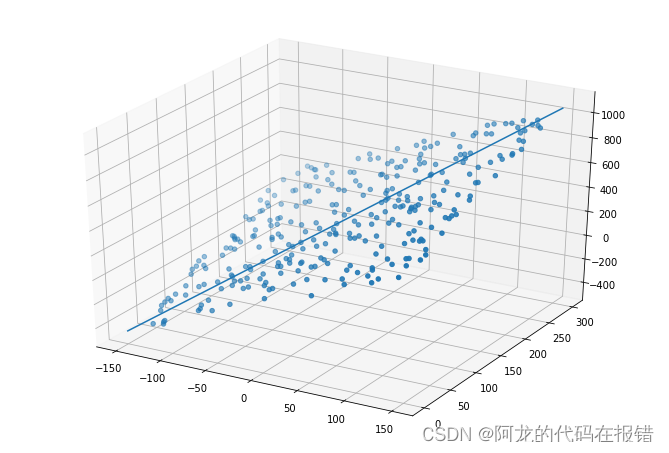
堅持學習，整理復盤