實驗7 K-means聚類實驗
一、實驗目的
學習K-means算法基本原理,實現Iris數據聚類。
二、實驗內容
應用K-means算法對iris數據集進行聚類。
三、實驗結果及分析
0:輸出數據集的基本信息
參考代碼在main函數中首先打印了數據、特征名字、目標值、目標值的名字,iris數據集的結果如下圖所示。
【數據】
??? 數據共有150組,每組包含4個特征。

【特征名字】
??? 每組數據包含的特征為:花萼長度、花萼寬度、花瓣長度、花瓣寬度。其中sepal對應花萼,而petal對應花瓣。

【目標值】
??? 數據集里面共包含3種鳶尾,標簽分別是0、1、2。由此可知,我們后面需要通過K-means算法聚成3類以進行分類。
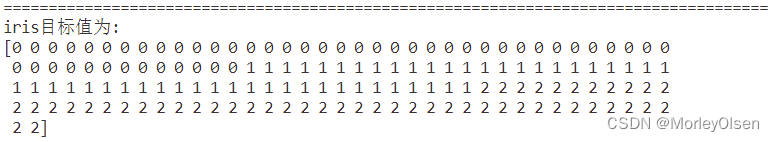
【目標值的名字】
數據集里面標簽分別為0、1、2的各組數據,類別分別對應setosa、versicolor、virginica。
同時,參考代碼中利用show_data函數,分別畫出了花萼長度和寬度的關系和花瓣長度和寬度的關系,結果如下圖所示。
【Sepal花萼】
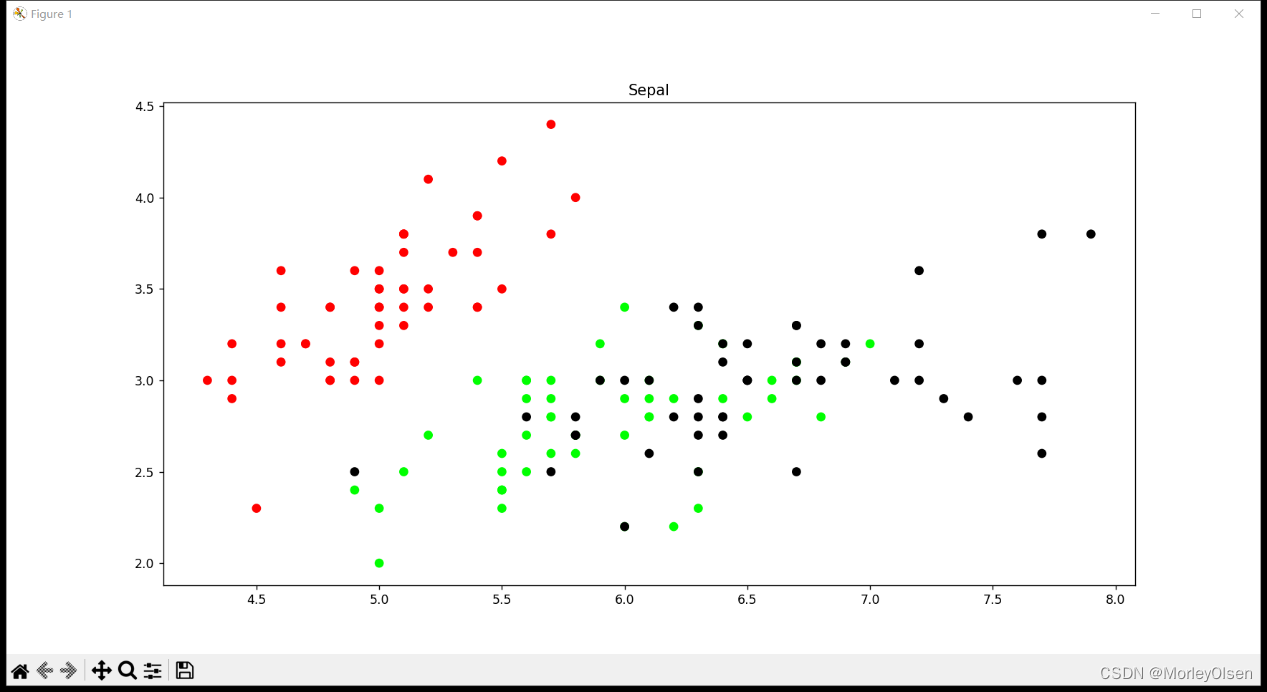
【Petal花瓣】
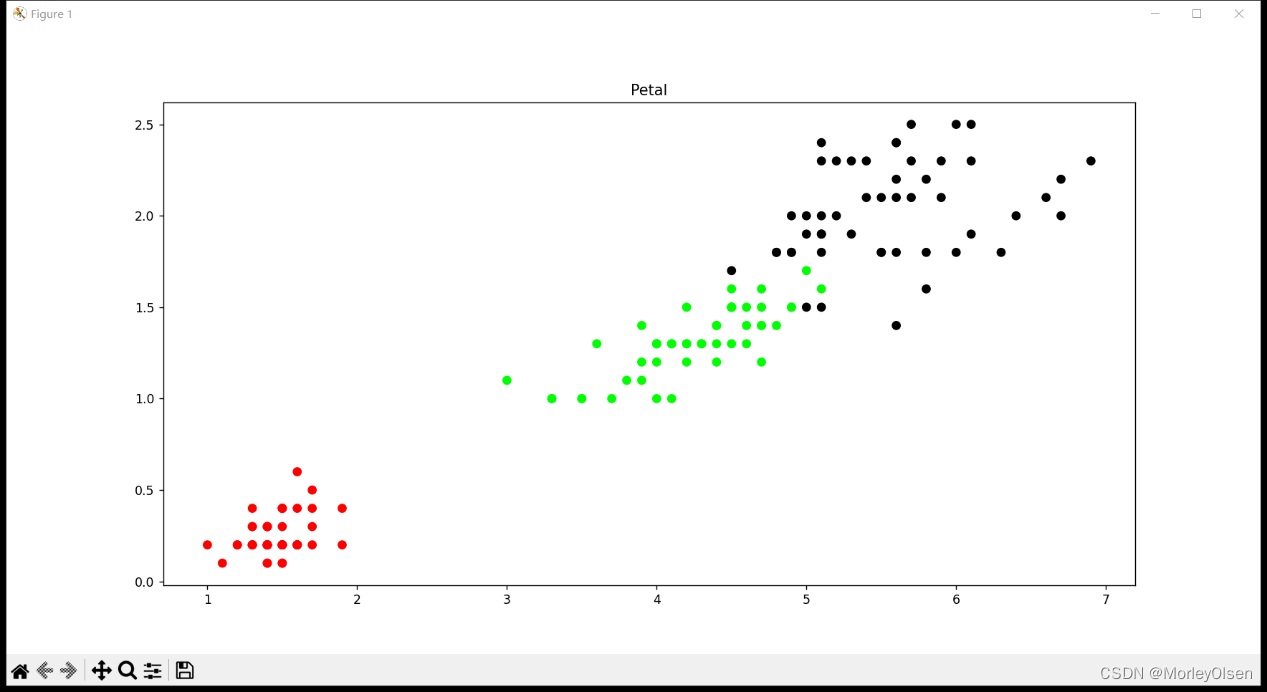
1:調用Kmeans進行聚類
在任務1中,需要分別對Sepal和Petal進行聚類。此處使用【sklearn】庫中的KMeans封裝包進行調用,選定初始的聚類數目為3,采用fit方法進行模型訓練,最后得到訓練標簽為【kmeans_sepal.labels_】和【kmeans_petal.labels_】。整體代碼如下圖所示。

同時,采用head方法輸出前幾個數據的聚類情況,程序輸出結果如下圖所示。
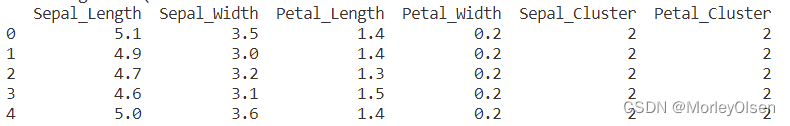
2:繪出聚類前后的圖
在任務2中, 我們定義了圖的大小,并定義了4個子圖,分別用于顯示花萼聚類前、花萼聚類后、花瓣聚類前、花瓣聚類后的聚類散點圖。整體代碼如下圖所示。
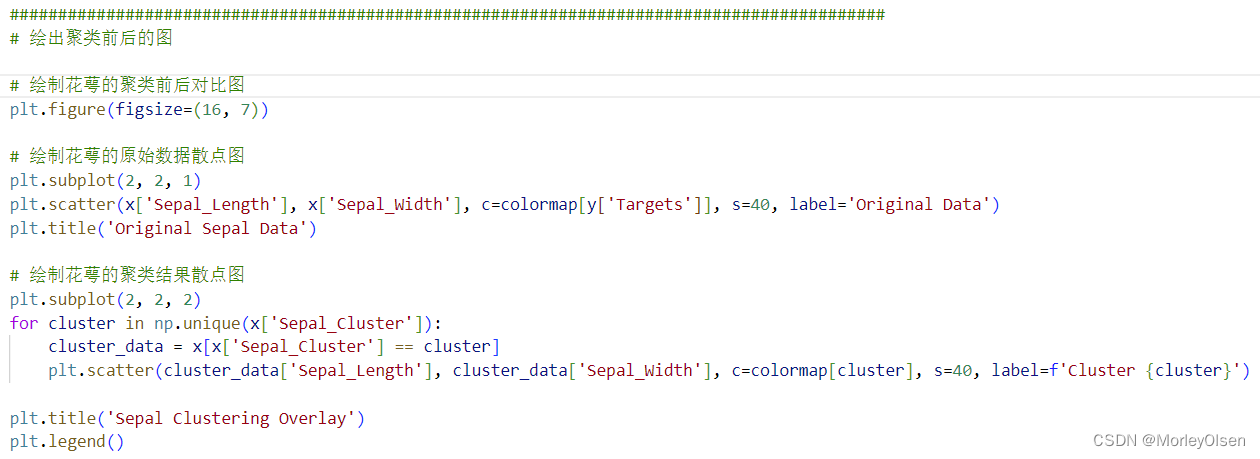

程序輸出結果如下圖所示。其中,Original Sepal Data對應原始花萼數據,Sepal Clustering Overlay對應聚類后的花萼數據,Original Petal Data對應原始花瓣數據,Petal Clustering Overlay對應聚類后的花瓣數據。

3:計算并輸出準確率
在任務3中,利用【from sklearn.metrics import accuracy_score】從評價指標中調用準確率,輸入數據集本身的標簽和kmeans算法聚類得到的標簽,進行對比后輸出準確率結果。整體代碼如下圖所示。

程序輸出結果如下圖所示。可以看到計算出來的花萼聚類的準確率為25.33%、花瓣聚類的準確率為1.33%。
![]()
通過任務2中的對比圖可知,原來的標簽與聚類結果的標簽所對應的關系如下表所示。其中,表格中的橘色位置處均是結果標簽與原始標簽存在不一致的情況。因此,該準確率存在不準確的情況,只有當原始標簽等于結果標簽時,才能得到正確的Accuracy。同時,應該采用適合非監督學習的評價指標進行結果優劣的判斷。
| 聚類對象 | 原始標簽 | 結果標簽 |
| 花萼 | 紅 | 黑 |
| 綠 | 綠 | |
| 黑 | 紅 | |
| 花瓣 | 紅 | 黑 |
| 綠 | 紅 | |
| 黑 | 綠 |
4:計算并輸出輪廓系數(自增)
在任務4中,利用【from sklearn.metrics import silhouette_score】從評價指標中調用輪廓系數,輸入數據集本身的特征值和kmeans算法聚類得到的標簽,進行對比后輸出輪廓系數結果。整體代碼如下圖所示。
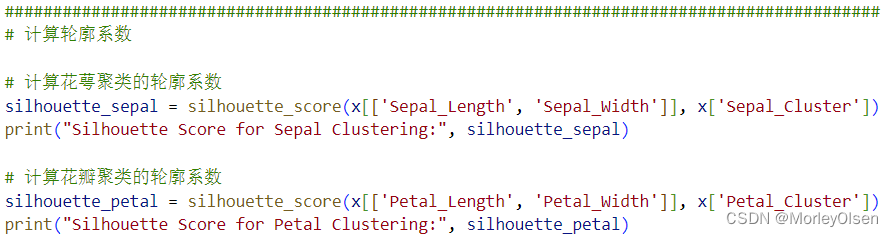
程序輸出結果如下圖所示。可以看到計算出來的花萼聚類的輪廓系數為0.45左右、花瓣聚類的輪廓系數為0.66左右。
![]()
5:計算并輸出Adjusted Rand Index(自增)
在任務5中,利用【from sklearn.metrics import adjusted_rand_score】從評價指標中調用ARI,輸入數據集本身的標簽和kmeans算法聚類得到的標簽,進行對比后輸出ARI結果。整體代碼如下圖所示。

?程序輸出結果如下圖所示。可以看到計算出來的花萼聚類的ARI為0.60左右、花瓣聚類的ARI為0.89左右。

四、遇到的問題和解決方案
問題1:每次執行時,K-means聚類算法計算出來的Accuracy均不同。
解決1:經過對比打印出的數據標簽和聚類標簽可知,K-means聚類算法在每次執行后給每一類分配的標簽不同,只具備一定的映射關系(例如dataset中的0標簽與kmeans-label中的1標簽相映射,而不是與kmeans-label中的0標簽對應)。但是不能保證每次代碼運行后的映射關系相同,因此需要采用ARI評價指標來評估聚類的好壞。
五、實驗總結和心得
1:KMeans包中可修改以下參數:n_clusters(指定要分成的簇的數量)、init(用于初始化簇中心的方法,可以選擇隨機初始值random,或從數據中選擇初始值k-means++)、n_init(執行K均值算法的次數)、max_iter(每次迭代的最大次數)、tol(收斂的閾值)、random_state(用于確定隨機種子的整數,以確保結果的可重復性)、algorithm(用于計算距離的算法,可以選擇full、elkan、auto等)、precompute_distances(指定是否預先計算距離,可以加速算法的收斂)。一般來說,最重要的是確定簇的數量 n_clusters,因為它會直接影響到聚類的結果。
2:ARI用于評估聚類結果與真實標簽之間的一致性,其取值范圍在[-1, 1]之間,越接近1表示聚類效果越好。
3:輪廓系數用于衡量數據點與其所屬簇內部的相似度和與其他簇之間的差異度,其取值范圍在[-1, 1]之間。輪廓系數接近1表示數據點與其所屬簇內的其他數據點非常相似,同時與其他簇的數據點差異很大,通常表示數據點被正確地分配到了合適的簇中。輪廓系數接近0表示數據點與其所屬簇內部的數據點相似度與其他簇的數據點相似度差不多,通常表示數據點可能位于兩個或多個簇的邊界上。輪廓系數接近-1表示數據點與其所屬簇內的其他數據點差異很大,但與其他簇的數據點相似度高,通常表示數據點被錯誤地分配到了不合適的簇中。輪廓系數可以用于選擇最佳的K值,比較不同聚類算法的性能,或者評估聚類結果的質量。
4:K均值聚類的主要思想是通過迭代尋找簇中心,將數據點分配到距離最近的簇中心。在應用聚類算法之前,可以進行實驗并評估聚類性能。通過可視化和指標評估,可以更好地理解數據的結構和選擇合適的K值。
六、附錄
(1)完整程序源代碼(含注釋)
各部分的任務操作在多行代碼注釋下構造。各段代碼含有概念注釋模塊。
| import matplotlib.pyplot as plt from sklearn import datasets from sklearn.cluster import KMeans import sklearn.metrics as sm import pandas as pd import numpy as np from sklearn.metrics import accuracy_score from sklearn.metrics import adjusted_rand_score from sklearn.metrics import silhouette_score def print_data(want_print, print_iris): ? ? """ ? ? 展示iris的數據 ? ? :return: None ? ? """ ? ? print("iris{0}為:\n{1}".format(want_print, print_iris)) ? ? print("=" * 85) ? def show_data(length, width, title): ? ? """ ? ? 畫圖 ? ? :param length: 長度 ? ? :param width: 寬度 ? ? :param title: 標題 ? ? :return: None ? ? """ ? ? # 建立一個畫布 ? ? plt.figure(figsize=(14, 7)) ? ? plt.scatter(length, width, c=colormap[y.Targets], s=40) ? ? plt.title(title) ? ? plt.show() if __name__ == '__main__': ? ? # 導入iris數據 ? ? iris = datasets.load_iris() ? ? # 展示iris真實數據 ? ? print_data(want_print="數據", print_iris=iris.data) ? ? # 展示iris特征名字 ? ? print_data(want_print="特征名字", print_iris=iris.feature_names) ? ? # 展示目標值 ? ? print_data(want_print="目標值", print_iris=iris.target) ? ? # 展示目標值的名字 ? ? print_data(want_print="目標值的名字", print_iris=iris.target_names) ? ? # 為了便于使用,將iris數據轉換為pandas庫數據結構,并設立列的名字 ? ? # 將iris數據轉為pandas數據結構 ? ? x = pd.DataFrame(iris.data) ? ? # 將iris數據的名字設為‘Sepal_Length’,‘Sepal_Width’,‘Sepal_Width’,‘Petal_Width’ ? ? x.columns = ['Sepal_Length', 'Sepal_Width', 'Petal_Length', 'Petal_Width'] ? ? # 將iris目標值也轉為pandas數據結構 ? ? y = pd.DataFrame(iris.target) ? ? # 將iris目標值得名字設為‘Targets’ ? ? y.columns = ['Targets'] ? ? # 創建色板圖 ? ? colormap = np.array(['red', 'lime', 'black']) ? ? # 開始畫Sepal長度和寬度的關系 ? ? show_data(length=x.Sepal_Length, width=x.Sepal_Width, title='Sepal') ? ? # 開始畫Petal長度和寬度的關系 ? ? show_data(length=x.Petal_Length, width=x.Petal_Width, title='Petal') ? ? ? ? ########################################################################################### ? ? # 調用Kmeans進行聚類 ? ? ? ? # for sepal ? ? kmeans_sepal = KMeans(n_clusters=3) ? ? kmeans_sepal.fit(x[['Sepal_Length', 'Sepal_Width']]) ? ? x['Sepal_Cluster'] = kmeans_sepal.labels_ ? ? # for petal ? ? kmeans_petal = KMeans(n_clusters=3) ? ? kmeans_petal.fit(x[['Petal_Length', 'Petal_Width']]) ? ? x['Petal_Cluster'] = kmeans_petal.labels_ ? ? # 打印前幾行數據(including聚類結果) ? ? print(x.head()) ? ? # print(y.Targets) ? ? ? ? ########################################################################################### ? ? # 計算輪廓系數 ? ? ? ? # 計算花萼聚類的輪廓系數 ? ? silhouette_sepal = silhouette_score(x[['Sepal_Length', 'Sepal_Width']], x['Sepal_Cluster']) ? ? print("Silhouette Score for Sepal Clustering:", silhouette_sepal) ? ? # 計算花瓣聚類的輪廓系數 ? ? silhouette_petal = silhouette_score(x[['Petal_Length', 'Petal_Width']], x['Petal_Cluster']) ? ? print("Silhouette Score for Petal Clustering:", silhouette_petal) ? ? ? ? ########################################################################################### ? ? # 繪出聚類前后的圖 ? ? ? ? # 繪制花萼的聚類前后對比圖 ? ? plt.figure(figsize=(16, 7)) ? ? # 繪制花萼的原始數據散點圖 ? ? plt.subplot(2, 2, 1) ? ? plt.scatter(x['Sepal_Length'], x['Sepal_Width'], c=colormap[y['Targets']], s=40, label='Original Data') ? ? plt.title('Original Sepal Data') ? ? # 繪制花萼的聚類結果散點圖 ? ? plt.subplot(2, 2, 2) ? ? for cluster in np.unique(x['Sepal_Cluster']): ? ? ? ? cluster_data = x[x['Sepal_Cluster'] == cluster] ? ? ? ? plt.scatter(cluster_data['Sepal_Length'], cluster_data['Sepal_Width'], c=colormap[cluster], s=40, label=f'Cluster {cluster}') ? ? plt.title('Sepal Clustering Overlay') ? ? plt.legend() ? ? # 繪制花瓣的聚類前后對比圖 ? ? # 繪制花瓣的原始數據散點圖 ? ? plt.subplot(2, 2, 3) ? ? plt.scatter(x['Petal_Length'], x['Petal_Width'], c=colormap[y['Targets']], s=40, label='Original Data') ? ? plt.title('Original Petal Data') ? ? # 繪制花瓣的聚類結果散點圖 ? ? plt.subplot(2, 2, 4) ? ? for cluster in np.unique(x['Petal_Cluster']): ? ? ? ? cluster_data = x[x['Petal_Cluster'] == cluster] ? ? ? ? plt.scatter(cluster_data['Petal_Length'], cluster_data['Petal_Width'], c=colormap[cluster], s=40, label=f'Cluster {cluster}') ? ? plt.title('Petal Clustering Overlay') ? ? plt.legend() ? ? plt.tight_layout() ? ? plt.show() ? ? ? ? ########################################################################################### ? ? # 計算并輸出Accuracy ? ? ? ? # acc for sepal ? ? accuracy_sepal = accuracy_score(iris.target, kmeans_sepal.labels_) ? ? print("Accuracy for Sepal Clustering: {:.2f}%".format(accuracy_sepal * 100)) ? ? ? ? # acc for petal ? ? accuracy_petal = accuracy_score(iris.target, kmeans_petal.labels_) ? ? print("Accuracy for Petal Clustering: {:.2f}%".format(accuracy_petal * 100)) ? ? ? ? ########################################################################################### ? ? # 計算并輸出ARI(adjusted_rand_score) ? ? """ ? ? ? ? ARI(Adjusted Rand Index): ? ? ? ? 用于評估聚類結果與真實標簽之間的一致性。取值范圍在[-1, 1]之間,越接近1表示聚類效果越好。 ? ? """ ? ? ? ? # ARI for sepal ? ? ari_score_sepal = adjusted_rand_score(iris.target, x['Sepal_Cluster']) ? ? print("ARI for Sepal Clustering:", ari_score_sepal) ? ? ? ? # ARI for petal ? ? ari_score_petal = adjusted_rand_score(iris.target, x['Petal_Cluster']) ? ? print("ARI for Petal Clustering:", ari_score_petal) |
(2)數據集文本文件
| "Sepal.Length" "Sepal.Width" "Petal.Length" "Petal.Width" "Species" "1" 5.1 3.5 1.4 0.2 "setosa" "2" 4.9 3 1.4 0.2 "setosa" "3" 4.7 3.2 1.3 0.2 "setosa" "4" 4.6 3.1 1.5 0.2 "setosa" "5" 5 3.6 1.4 0.2 "setosa" "6" 5.4 3.9 1.7 0.4 "setosa" "7" 4.6 3.4 1.4 0.3 "setosa" "8" 5 3.4 1.5 0.2 "setosa" "9" 4.4 2.9 1.4 0.2 "setosa" "10" 4.9 3.1 1.5 0.1 "setosa" "11" 5.4 3.7 1.5 0.2 "setosa" "12" 4.8 3.4 1.6 0.2 "setosa" "13" 4.8 3 1.4 0.1 "setosa" "14" 4.3 3 1.1 0.1 "setosa" "15" 5.8 4 1.2 0.2 "setosa" "16" 5.7 4.4 1.5 0.4 "setosa" "17" 5.4 3.9 1.3 0.4 "setosa" "18" 5.1 3.5 1.4 0.3 "setosa" "19" 5.7 3.8 1.7 0.3 "setosa" "20" 5.1 3.8 1.5 0.3 "setosa" "21" 5.4 3.4 1.7 0.2 "setosa" "22" 5.1 3.7 1.5 0.4 "setosa" "23" 4.6 3.6 1 0.2 "setosa" "24" 5.1 3.3 1.7 0.5 "setosa" "25" 4.8 3.4 1.9 0.2 "setosa" "26" 5 3 1.6 0.2 "setosa" "27" 5 3.4 1.6 0.4 "setosa" "28" 5.2 3.5 1.5 0.2 "setosa" "29" 5.2 3.4 1.4 0.2 "setosa" "30" 4.7 3.2 1.6 0.2 "setosa" "31" 4.8 3.1 1.6 0.2 "setosa" "32" 5.4 3.4 1.5 0.4 "setosa" "33" 5.2 4.1 1.5 0.1 "setosa" "34" 5.5 4.2 1.4 0.2 "setosa" "35" 4.9 3.1 1.5 0.2 "setosa" "36" 5 3.2 1.2 0.2 "setosa" "37" 5.5 3.5 1.3 0.2 "setosa" "38" 4.9 3.6 1.4 0.1 "setosa" "39" 4.4 3 1.3 0.2 "setosa" "40" 5.1 3.4 1.5 0.2 "setosa" "41" 5 3.5 1.3 0.3 "setosa" "42" 4.5 2.3 1.3 0.3 "setosa" "43" 4.4 3.2 1.3 0.2 "setosa" "44" 5 3.5 1.6 0.6 "setosa" "45" 5.1 3.8 1.9 0.4 "setosa" "46" 4.8 3 1.4 0.3 "setosa" "47" 5.1 3.8 1.6 0.2 "setosa" "48" 4.6 3.2 1.4 0.2 "setosa" "49" 5.3 3.7 1.5 0.2 "setosa" "50" 5 3.3 1.4 0.2 "setosa" "51" 7 3.2 4.7 1.4 "versicolor" "52" 6.4 3.2 4.5 1.5 "versicolor" "53" 6.9 3.1 4.9 1.5 "versicolor" "54" 5.5 2.3 4 1.3 "versicolor" "55" 6.5 2.8 4.6 1.5 "versicolor" "56" 5.7 2.8 4.5 1.3 "versicolor" "57" 6.3 3.3 4.7 1.6 "versicolor" "58" 4.9 2.4 3.3 1 "versicolor" "59" 6.6 2.9 4.6 1.3 "versicolor" "60" 5.2 2.7 3.9 1.4 "versicolor" "61" 5 2 3.5 1 "versicolor" "62" 5.9 3 4.2 1.5 "versicolor" "63" 6 2.2 4 1 "versicolor" "64" 6.1 2.9 4.7 1.4 "versicolor" "65" 5.6 2.9 3.6 1.3 "versicolor" "66" 6.7 3.1 4.4 1.4 "versicolor" "67" 5.6 3 4.5 1.5 "versicolor" "68" 5.8 2.7 4.1 1 "versicolor" "69" 6.2 2.2 4.5 1.5 "versicolor" "70" 5.6 2.5 3.9 1.1 "versicolor" "71" 5.9 3.2 4.8 1.8 "versicolor" "72" 6.1 2.8 4 1.3 "versicolor" "73" 6.3 2.5 4.9 1.5 "versicolor" "74" 6.1 2.8 4.7 1.2 "versicolor" "75" 6.4 2.9 4.3 1.3 "versicolor" "76" 6.6 3 4.4 1.4 "versicolor" "77" 6.8 2.8 4.8 1.4 "versicolor" "78" 6.7 3 5 1.7 "versicolor" "79" 6 2.9 4.5 1.5 "versicolor" "80" 5.7 2.6 3.5 1 "versicolor" "81" 5.5 2.4 3.8 1.1 "versicolor" "82" 5.5 2.4 3.7 1 "versicolor" "83" 5.8 2.7 3.9 1.2 "versicolor" "84" 6 2.7 5.1 1.6 "versicolor" "85" 5.4 3 4.5 1.5 "versicolor" "86" 6 3.4 4.5 1.6 "versicolor" "87" 6.7 3.1 4.7 1.5 "versicolor" "88" 6.3 2.3 4.4 1.3 "versicolor" "89" 5.6 3 4.1 1.3 "versicolor" "90" 5.5 2.5 4 1.3 "versicolor" "91" 5.5 2.6 4.4 1.2 "versicolor" "92" 6.1 3 4.6 1.4 "versicolor" "93" 5.8 2.6 4 1.2 "versicolor" "94" 5 2.3 3.3 1 "versicolor" "95" 5.6 2.7 4.2 1.3 "versicolor" "96" 5.7 3 4.2 1.2 "versicolor" "97" 5.7 2.9 4.2 1.3 "versicolor" "98" 6.2 2.9 4.3 1.3 "versicolor" "99" 5.1 2.5 3 1.1 "versicolor" "100" 5.7 2.8 4.1 1.3 "versicolor" "101" 6.3 3.3 6 2.5 "virginica" "102" 5.8 2.7 5.1 1.9 "virginica" "103" 7.1 3 5.9 2.1 "virginica" "104" 6.3 2.9 5.6 1.8 "virginica" "105" 6.5 3 5.8 2.2 "virginica" "106" 7.6 3 6.6 2.1 "virginica" "107" 4.9 2.5 4.5 1.7 "virginica" "108" 7.3 2.9 6.3 1.8 "virginica" "109" 6.7 2.5 5.8 1.8 "virginica" "110" 7.2 3.6 6.1 2.5 "virginica" "111" 6.5 3.2 5.1 2 "virginica" "112" 6.4 2.7 5.3 1.9 "virginica" "113" 6.8 3 5.5 2.1 "virginica" "114" 5.7 2.5 5 2 "virginica" "115" 5.8 2.8 5.1 2.4 "virginica" "116" 6.4 3.2 5.3 2.3 "virginica" "117" 6.5 3 5.5 1.8 "virginica" "118" 7.7 3.8 6.7 2.2 "virginica" "119" 7.7 2.6 6.9 2.3 "virginica" "120" 6 2.2 5 1.5 "virginica" "121" 6.9 3.2 5.7 2.3 "virginica" "122" 5.6 2.8 4.9 2 "virginica" "123" 7.7 2.8 6.7 2 "virginica" "124" 6.3 2.7 4.9 1.8 "virginica" "125" 6.7 3.3 5.7 2.1 "virginica" "126" 7.2 3.2 6 1.8 "virginica" "127" 6.2 2.8 4.8 1.8 "virginica" "128" 6.1 3 4.9 1.8 "virginica" "129" 6.4 2.8 5.6 2.1 "virginica" "130" 7.2 3 5.8 1.6 "virginica" "131" 7.4 2.8 6.1 1.9 "virginica" "132" 7.9 3.8 6.4 2 "virginica" "133" 6.4 2.8 5.6 2.2 "virginica" "134" 6.3 2.8 5.1 1.5 "virginica" "135" 6.1 2.6 5.6 1.4 "virginica" "136" 7.7 3 6.1 2.3 "virginica" "137" 6.3 3.4 5.6 2.4 "virginica" "138" 6.4 3.1 5.5 1.8 "virginica" "139" 6 3 4.8 1.8 "virginica" "140" 6.9 3.1 5.4 2.1 "virginica" "141" 6.7 3.1 5.6 2.4 "virginica" "142" 6.9 3.1 5.1 2.3 "virginica" "143" 5.8 2.7 5.1 1.9 "virginica" "144" 6.8 3.2 5.9 2.3 "virginica" "145" 6.7 3.3 5.7 2.5 "virginica" "146" 6.7 3 5.2 2.3 "virginica" "147" 6.3 2.5 5 1.9 "virginica" "148" 6.5 3 5.2 2 "virginica" "149" 6.2 3.4 5.4 2.3 "virginica" "150" 5.9 3 5.1 1.8 "virginica" |
)




 - 區塊鏈期刊:Distributed Ledger Technologies: Research and Practice)



![[ROS2] --- action](http://pic.xiahunao.cn/[ROS2] --- action)





實現小程序端圖表,并修改源碼簡化使用)



 和 wait() 有什么區別?)