概率密度函數(PDF)是一個描述連續隨機變量取特定值的相對可能性的函數。對于正態分布的情況,其PDF有一個特定的形式,這個形式中包括了一個常數乘以一個指數函數,它假設誤差項服從均值為0的正態分布:
p ( ? ( i ) ) = 1 2 π σ 2 exp ? ( ? ( ? ( i ) ) 2 2 σ 2 ) p(\epsilon^{(i)}) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(\epsilon^{(i)})^2}{2\sigma^2}\right) p(?(i))=2πσ2?1?exp(?2σ2(?(i))2?)
各名詞解釋:
p ( ? ( i ) ) p(\epsilon^{(i)}) p(?(i)):這部分表示給定誤差 ? ( i ) \epsilon^{(i)} ?(i)的概率密度。
σ 2 \sigma^2 σ2:正態分布的形狀完全由兩個參數決定:均值( μ \mu μ)和方差( σ 2 \sigma^2 σ2)。均值決定了分布的中心位置,而方差(標準差的平方)決定了分布的離散程度。這里均值( μ \mu μ)都假設為0因此不討論。詳細解釋一下 σ 2 \sigma^2 σ2:
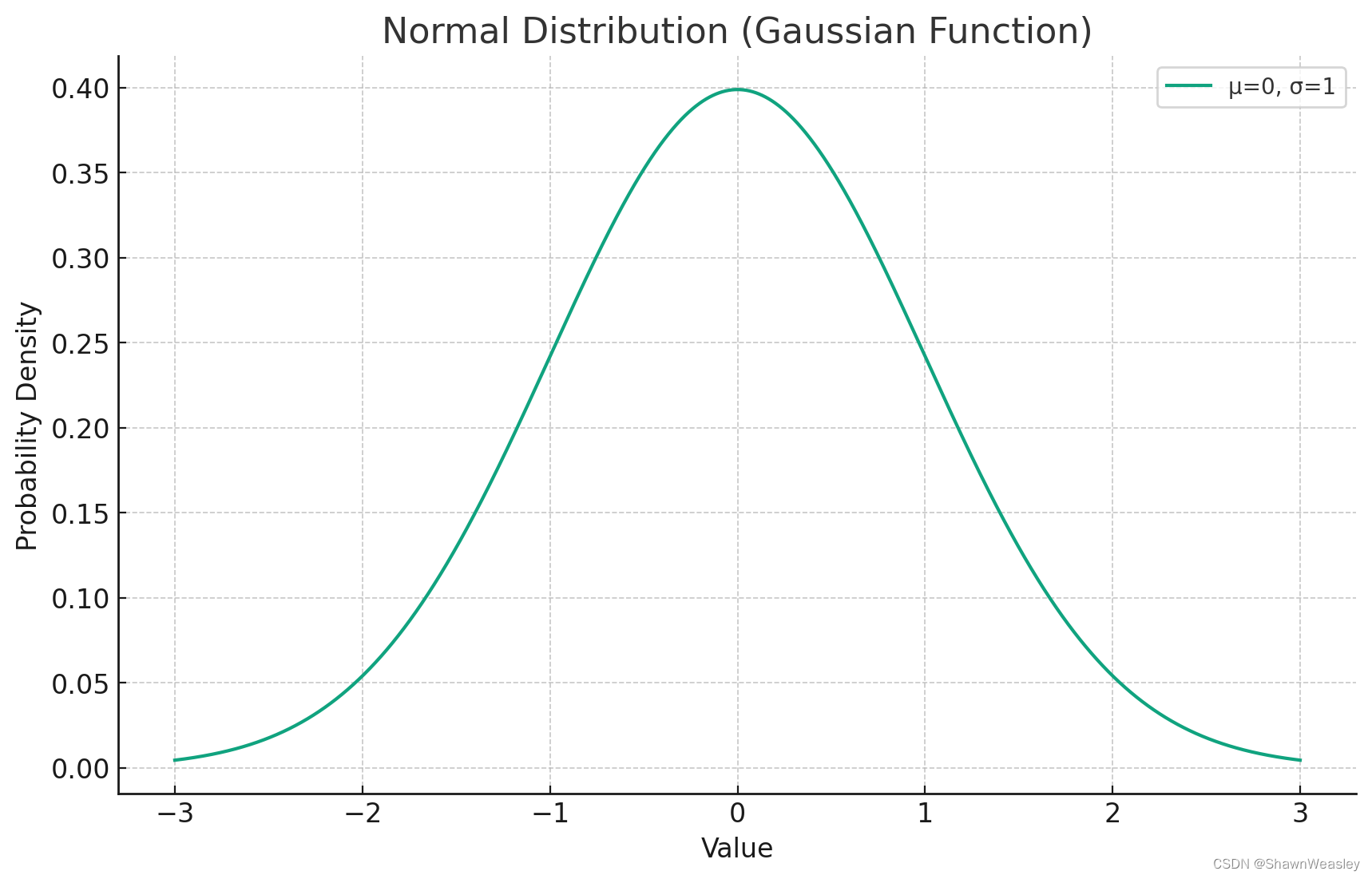
- σ 2 \sigma^2 σ2是分布寬度的度量, σ 2 \sigma^2 σ2的數值表示數據分布的離散程度: σ 2 \sigma^2 σ2越大,數據分布越分散; σ 2 \sigma^2 σ2越小,數據分布越集中(如上圖中的鐘形越瘦)。
- σ 2 \sigma^2 σ2的計算過程:
a.假設你有一組數據 X = { x 1 , x 2 , . . . , x n } X = \{x_1, x_2, ..., x_n\} X={x1?,x2?,...,xn?},且已知均值 μ \mu μ為0。
b.計算每個數據點的平方: x i 2 x_i^2 xi2?計算了每個數據點距離均值(0)的距離的平方。
c.計算這些平方的平均值(即方差 σ 2 \sigma^2 σ2): σ 2 = 1 n ∑ i = 1 n x i 2 \sigma^2 = \frac{1}{n} \sum_{i=1}^{n} x_i^2 σ2=n1?∑i=1n?xi2?(即 x i 2 x_i^2 xi2?求和后平均)
1 2 π σ 2 \frac{1}{\sqrt{2\pi\sigma^2}} 2πσ2?1?:這是正態分布概率密度函數的前綴,其中 σ 2 \sigma^2 σ2是方差。它的作用是確保概率密度函數(PDF)的積分——也就是函數下整個面積等于1。在數學上,這意味著對于連續概率分布,確保所有概率值的總和為1。
exp: e e e是一個重要的數學常數(自然對數的底數),約等于2.71828,而exp是 e e e的冪。exp用于計算概率的指數部分,確保了大多數數據點都集中在平均值附近,而遠離均值的數據點則呈指數級減少,就是讓曲線呈“鐘形曲線(高斯分布)”。
? ( ? ( i ) ) 2 2 σ 2 -\frac{(\epsilon^{(i)})^2}{2\sigma^2} ?2σ2(?(i))2?:這是exp指數函數內的冪,代表了 ? ( i ) \epsilon^{(i)} ?(i)偏離均值0的程度。
- 由于我們假設誤差項 ? \epsilon ?均值為0,所以這里直接用 ? ( i ) \epsilon^{(i)} ?(i)。這個比例的平方表示了誤差項的值距離均值(0)的距離的平方,然后除以 2 σ 2 {2\sigma^2} 2σ2來“標準化”這個距離。在正態分布中,這個距離的平方越大,觀測到該誤差的概率就越低。
- 這個過程與誤差項 ? ( i ) \epsilon^{(i)} ?(i)的值(第 i i i個數據點的誤差項)的平方成正比,這里的平方是必要的,因為我們對誤差的大小感興趣,而不管它是正的還是負的。平方確保了所有的誤差值都是非負的,且更大的誤差(無論正負)都會產生更大的平方值。
- 與方差 σ 2 {\sigma^2} σ2的兩倍成反比,這里 σ 2 {\sigma^2} σ2表示整個數據集中的誤差項的分布寬度。方差的兩倍是概率密度函數的標準組成部分,用于“標準化”誤差項的平方,這樣不同的分布(具有不同的方差)就可以使用相同的函數形式。這里的乘以 1 2 σ 2 \frac{1}{2\sigma^2} 2σ21?類似于計算出“相對”值而不是“絕對”值,在不改變誤差項的方向的情況下,調整它的相對重要性。主要作用是:由于不同的數據集可能有不同的方差(即不同的誤差分布寬度),我們需要有一種方式來標準化這些誤差,使它們可以在統一的尺度上比較。
- ? 1 2 σ 2 -\frac{1}{2\sigma^2} ?2σ21?:這個負號和分母 2 σ 2 {2\sigma^2} 2σ2一起工作,形成一個比例因子,表示一個衰減的過程,它反映了誤差項 ? ( i ) \epsilon^{(i)} ?(i)相對于方差的大小。由于是負指數,誤差項的平方越大, e e e的冪就越小,從而降低了該誤差值的概率密度。

——軟件安裝與使用(3))






嵌入式程序任務調度的設計)








)

