相關資料

李沐 動手學深度學習

優化算法

優化算法使我們能夠繼續更新模型參數，并使損失函數的值最小化。優化算法的性能直接影響模型的訓練效率。

優化問題中大多數目標函數都很復雜，沒有解析解。相反，必須使用數值優化算法。

• 優化與深度學習之間的關系
  • 優化和深度學習的目標是根本不同的。前者關注的是最小化目標，后者則關注在給定有限數量的情況下尋找合適的模型。
  • 訓練誤差和泛化誤差通常不同：由于優化算法的目標函數通常是基于訓練數據集的損失函數，因此優化的目標是減少訓練誤差。但是，深度學習（或更廣義地說，統計推斷）的目標是減少泛化誤差。為了實現后者，除了使用優化算法來減少訓練誤差之外，我們還需要注意過擬合。
• 深度學習中使用優化的挑戰
  • 這里關注局部最小值、鞍點和梯度消失
    • 鞍點：saddle point, 函數的所有梯度都消失但不是全局最小值也不是局部最小值的任何位置。較高維度的鞍點可能會更加隱蔽。
      
    • 梯度消失。假設我們想最小化函數 $$f(x)=tanh(x)$$
      ，然后我們恰好從 x=4 開始。正如我們所看到的那樣，f 的梯度接近零。更具體地說，$f^{{}^{\prime }}(x)=1?tan{h}^2(x)$，因此 $f^{{}^{\prime }}(4)=0.0013$.
      

懲罰的概念

梯度下降

在凸問題背景下設計和分析算法是非常有啟發性的。
凸優化的入門，以及凸目標函數上非常簡單的隨機梯度下降算法的證明。
為什么梯度下降算法可以優化目標函數？

學習率

學習率（learning rate）決定目標函數能否收斂到局部最小值，以及何時收斂到最小值。

牛頓法

隨機梯度下降

目標函數通常是訓練數據集中每個樣本的損失函數的平均值。

給定 n 個樣本的訓練數據集，我們假設 $f_i(x)$是關于索引 $i$ 的訓練樣本的損失函數，其中 $X$ 是參數向量。然后我們得到目標函數
$X$的目標函數的梯度計算為

其中$\mu$是學習率。我們可以看到，每次迭代的計算代價從梯度下降的$O(n)$降至常數$O(1)$.

小批量隨機梯度下降

動量法

這個動量法似乎不是針對學習率的改變。而是針對每個 $x_i$ 的值。

動量法可以解決變量之間梯度變化不一致導致的一些問題：

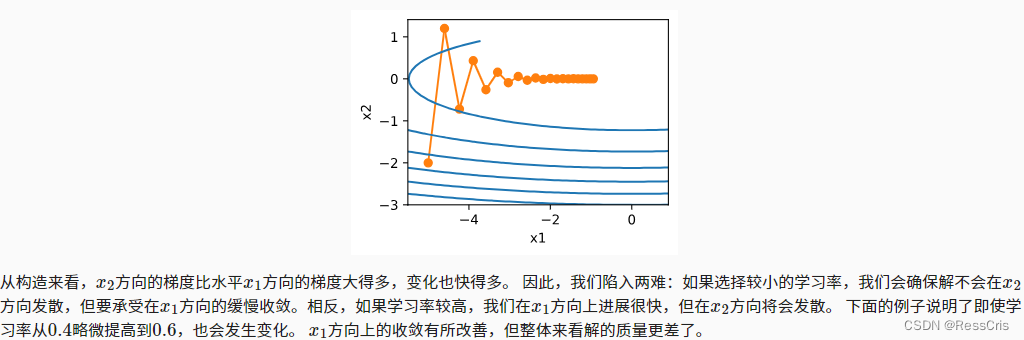
動量法解決上述問題

AdaGrad 算法

在AdaGrad算法中，我們允許每個坐標有單獨的學習率。

然而，在深度學習中，我們可能希望更慢地降低學習率。 這引出了許多AdaGrad算法的變體。
優化算法本身會根據梯度調節其實際的學習率。

RMSProp算法

以RMSProp算法作為將速率調度與坐標自適應學習率分離的簡單修復方法。

Adam

學習率調度器

多項式衰減
分段常數表

余弦學習率調度

它所依據的觀點是：我們可能不想在一開始就太大地降低學習率，而且可能希望最終能用非常小的學習率來“改進”解決方案。

預熱

在某些情況下，初始化參數不足以得到良好的解。 這對某些高級網絡設計來說尤其棘手，可能導致不穩定的優化結果。 對此，一方面，我們可以選擇一個足夠小的學習率， 從而防止一開始發散，然而這樣進展太緩慢。 另一方面，較高的學習率最初就會導致發散。

解決這種困境的一個相當簡單的解決方法是使用預熱期，在此期間學習率將增加至初始最大值，然后冷卻直到優化過程結束。

class CosineScheduler:def __init__(self, max_update, base_lr=0.01, final_lr=0,warmup_steps=0, warmup_begin_lr=0):self.base_lr_orig = base_lrself.max_update = max_updateself.final_lr = final_lrself.warmup_steps = warmup_stepsself.warmup_begin_lr = warmup_begin_lrself.max_steps = self.max_update - self.warmup_stepsdef get_warmup_lr(self, epoch):increase = (self.base_lr_orig - self.warmup_begin_lr) \* float(epoch) / float(self.warmup_steps)return self.warmup_begin_lr + increasedef __call__(self, epoch):if epoch < self.warmup_steps:return self.get_warmup_lr(epoch)if epoch <= self.max_update:self.base_lr = self.final_lr + (self.base_lr_orig - self.final_lr) * (1 + math.cos(math.pi * (epoch - self.warmup_steps) / self.max_steps)) / 2return self.base_lrscheduler = CosineScheduler(max_update=20, base_lr=0.3, final_lr=0.01)
d2l.plot(torch.arange(num_epochs), [scheduler(t) for t in range(num_epochs)])scheduler = CosineScheduler(20, warmup_steps=5, base_lr=0.3, final_lr=0.01)
d2l.plot(torch.arange(num_epochs), [scheduler(t) for t in range(num_epochs)])