---

前言

在本文章中，我們將要詳細介紹一下LeetcodeLCR 090. 打家劫舍 II。采用動態規劃解決，這是一道經典的多狀態dp問題

一、題目分析

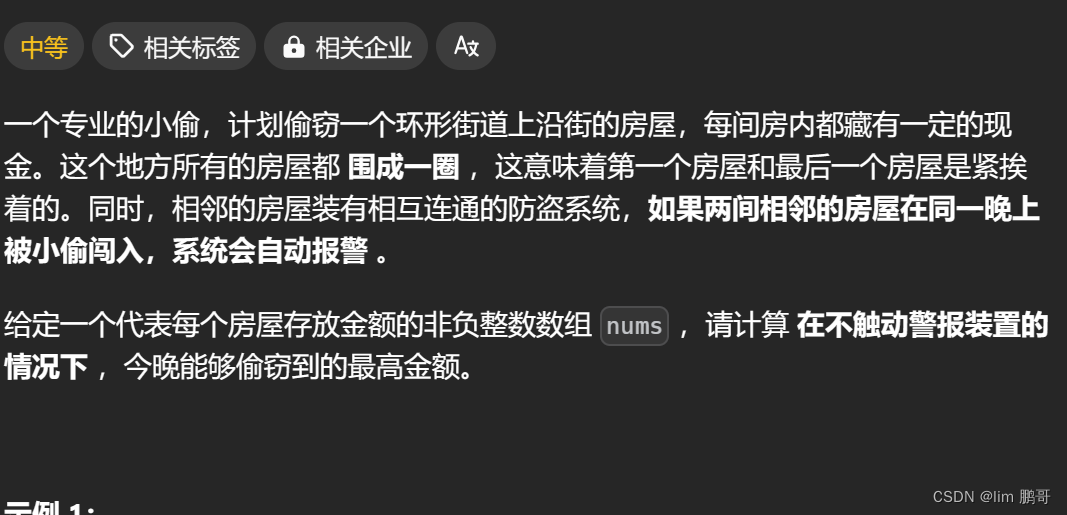
計算小偷能偷到的最大金額數，并且題目規定：
??🥉.兩個相鄰的房屋不能被偷
??🥉.第一個房屋和最后一個房屋不能被偷
規定1比較好解決，對于規定2，我們采用分情況討論的方法解決
??🍔.第一個房間偷，第二個房間和最后一個不被偷，在（2，n-2）下標之間尋找最大金額，再加上nums[0].
??🍔.第一個房間不被偷，最后一個房間不確定，在（1，n-1）下標之間尋找最大金額
??🍔.二者取最大值，就是題目所返回的值

二、算法原理

1.狀態表示

列出dp表，dp表中值的含義是什么
這可以細分為兩個表，因為經過該房間時不確定偷與不偷
???? .f[i]表示到達i房間時，資金被偷
????.g[i]表示到達i房間時，資金沒有被偷

2.狀態轉移方程

根據最近一步劃分問題
??🌟 f[i]:i位置被偷，那么根據題目規定，i-1位置就不能被偷，這不就正好是g[i-1],再加上i位置被偷的資金;
??🌟g[i]:i位置沒有被偷，i-1位置我們不確定有沒有被偷，所以需要分為兩種情況，這兩種情況取最大值
????🐧.i-1位置也沒有被偷，就是g[i-1]
????🐧.i-1位置被偷了，就是f[i-1]
結論：
??f[i]=g[i-1]+nums[i];
??g[i]=max(g[i-1],f[i-1])

3.初始化

保證填表不越界
??f[1]需要g[0]的值；g[1]需要g[0]和f[0]的值, 所以需要初始化g[0]和f[0].
??不用開辟額外的空間，這道題目的初始化很簡單。
注意：數組的下標和邊界條件

4.填表順序

兩個表一起填，從左往右

5.返回值是什么

max(f[n-1],g[n-1]);

三、代碼實現

class Solution {
public:int massage(vector<int>& nums,int left,int right) {if(left>right){return 0;}//建表int n=nums.size();int f[n];int g[n];//初始化for(int i=0;i<n;i++){f[i]=g[i]=0;}f[left]=nums[left];g[0]=0;//填表for(int i=left;i<=right;i++){f[i]=g[i-1]+nums[i];g[i]=max(g[i-1],f[i-1]);}//返回值return max(f[right],g[right]);}int rob(vector<int>& nums) {int  n=nums.size();//下標int ret1=massage(nums,2,n-2)+nums[0];int ret2=massage(nums,1,n-1);return max(ret1,ret2);}
};

總結

以上就是我們對LeetcodeLCR 090. 打家劫舍 II(leetcode)詳細介紹，希望對大家的學習有所幫助，僅供參考 如有錯誤請大佬指點我會盡快去改正 歡迎大家來評論~~