1466. 重新規劃路線

n 座城市，從 0 到 n-1 編號，其間共有 n-1 條路線。因此，要想在兩座不同城市之間旅行只有唯一一條路線可供選擇（路線網形成一顆樹）。去年，交通運輸部決定重新規劃路線，以改變交通擁堵的狀況。

路線用 connections 表示，其中 connections[i] = [a, b] 表示從城市 a 到 b 的一條有向路線。

今年，城市 0 將會舉辦一場大型比賽，很多游客都想前往城市 0 。

請你幫助重新規劃路線方向，使每個城市都可以訪問城市 0 。返回需要變更方向的最小路線數。

題目數據 保證 每個城市在重新規劃路線方向后都能到達城市 0 。

示例 1：

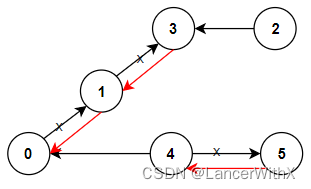
輸入：n = 6, connections = [[0,1],[1,3],[2,3],[4,0],[4,5]]
輸出：3
解釋：更改以紅色顯示的路線的方向，使每個城市都可以到達城市 0 。
示例 2：

輸入：n = 5, connections = [[1,0],[1,2],[3,2],[3,4]]
輸出：2
解釋：更改以紅色顯示的路線的方向，使每個城市都可以到達城市 0 。
示例 3：

輸入：n = 3, connections = [[1,0],[2,0]]
輸出：0

提示：

2 <= n <= 5 * 10^4
connections.length == n-1
connections[i].length == 2
0 <= connections[i][0], connections[i][1] <= n-1
connections[i][0] != connections[i][1]

有兩種解法，BFS或者DFS:

DFS解法

參考力扣官方解法：
思路與算法

題目給定一張由 nnn 個點（使用 000 到 n?1n-1n?1 編號），n?1n-1n?1 條邊構成的有向圖，如果忽略邊的方向，就變成了一棵樹。我們需要改變某些邊的方向使得每個點都可以訪問到 000 號點。

如果忽略邊的方向，將每條有向邊以及其反向邊加入到圖中，那么從任意一點出發都能到達 000 號點。路徑上可能會經過反向邊，我們需要變更與之對應的原邊的方向。需要變更的次數即為答案。

以每個點為起點進行搜索的代價會很大，因此我們考慮從 000 出發去遍歷其他點（可以使用深度優先搜索或者廣度優先搜索，本題解使用深度優先搜索），原來我們需要統計反向邊的數量，現在需要統計原方向邊的數量。

具體而言，我們使用 111 標記原方向的邊，使用 000 標記反向邊。然后從 000 號點開始遍歷，訪問到某個新的點時，所經過的邊被 111 標記，就令答案加 111。最終統計得到的答案就是我們需要變更方向的最小路線數。

class Solution {
public:int dfs(int x, int parent, vector<vector<pair<int, int>>>& e) {int res = 0;for (auto &edge : e[x]) {if (edge.first == parent) {continue;}res += edge.second + dfs(edge.first, x, e);}return res;}int minReorder(int n, vector<vector<int>>& connections) {vector<vector<pair<int, int>>> e(n);for (auto edge : connections) {e[edge[0]].push_back(make_pair(edge[1], 1));e[edge[1]].push_back(make_pair(edge[0], 0));}return dfs(0, -1, e);}
};

以下是我的解法 BFS

當我們面對這個問題時，我們的目標是重新規劃路線方向，使得每個城市都能到達城市 0。給定的城市和路線信息可以表示成一個有向圖，其中每個節點是城市，每條邊是一條有向的路線。為了達到目標，我們需要確保從每個城市到城市 0 都有一條有向路徑。
所以方法很明顯了 ，首先建立有向圖，然后bfs遍歷再計算反向邊數即可：

class Solution {
public:int minReorder(int n, std::vector<std::vector<int>>& connections) {std::vector<std::vector<std::pair<int, int>>> graph(n); // 使用鄰接表表示有向圖// 構建有向圖for (const auto& edge : connections) {graph[edge[0]].emplace_back(edge[1], 1);   // 原方向graph[edge[1]].emplace_back(edge[0], 0);   // 反方向}std::vector<bool> visited(n, false);int minReorderCount = 0;// 從城市0開始執行BFS遍歷std::queue<int> q;q.push(0);visited[0] = true;while (!q.empty()) {int currentCity = q.front();q.pop();for (const auto& neighbor : graph[currentCity]) {int nextCity = neighbor.first;int direction = neighbor.second;if (!visited[nextCity]) {// 如果需要反轉邊的方向，增加計數minReorderCount += direction;// 移動到BFS遍歷中的下一個城市q.push(nextCity);visited[nextCity] = true;}}}return minReorderCount;}
};