最優化方法復習——線性規劃之對偶問題

一、線性規劃對偶問題定義

原問題：

$\begin{gathered} (LP)\mathrm{Max}\quad z=c^\top x \\ \quad \quad s.t. \quad Ax \leq b \\ \quad \quad \quad \quad x \geq 0 \\ \end{gathered}$

對偶問題：

$\begin{gathered}(DP)\mathrm{Min}\quad f=b^\top y \\ \quad \quad s.t. \quad A^\top y\geq c \\ \quad \quad \quad \quad y\geq0 \\ \end{gathered}$

（1）若一個模型為目標求 “極大”，約束為“小于等于” 的不等式，則它的對偶模型為目標求“極小”，約束是“大于等于”的不等式。即“Max， ≤”和“Min，≥”相對應。

（2）從約束系數矩陣看：一個模型中為Ａ，則另一個模型中為AT 。一個模型是m個約束、 n個變量，則它的對偶模型為 n個約束、m個變量。

（3）從數據b、c的位置看：在兩個規劃模型中，b和c的位置對換。

（4）兩個規劃模型中的變量皆非負。

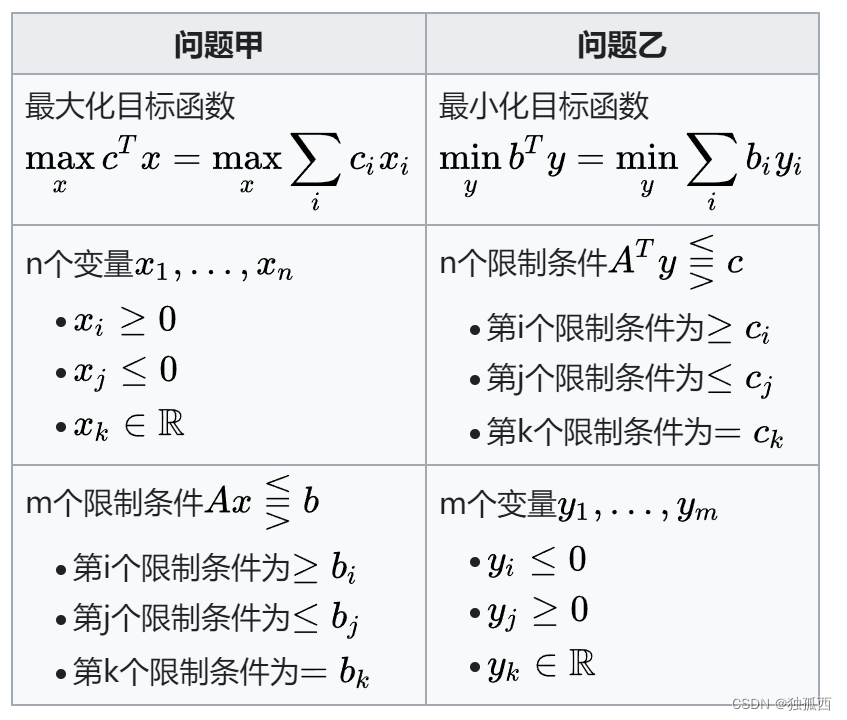
一般稱不具有對稱形式的一對線性規劃為非對稱形式的對偶規劃。對于非對稱形式的規劃，可以按照下面的對應關系直接給出其對偶規劃。

（1）將模型統一為“Max，≤”或“Min，≥” 的形式，對于其中的等式約束按下面（2）、（3）中的方法處理。

（2）若原規劃的某個約束條件為等式約束，則在對偶規劃中與此約束對應的那個變量取值沒有非負限制。

（3）若原規劃的某個變量的值沒有非負限制，則在對偶問題中與此變量對應的那個約束為等式。

二、對偶定理與影子價格

定理(弱對偶定理）若 x,y 分別為（LP) 和（DP）的可行解，那么 $c^Tx \leq b^Ty$ 。推論:設（LP）有可行解，那么若（LP）無有界最優解，則（DP）無可行解。
定理 (最優性準則定理) 若 $x^*$ , $y^*$ 分別(LP),(DP)的可行解,且 $c^Tx^* =b^Ty^*$ ，那么 $x^*$ , $y^*$ 分別為(LP)和(DP) 的最優解。
定理(主對偶定理) 若(LP)有最優解，則(DP)也有最優解。反之也成立，且最優值相等。

影子價格是一個向量，它的分量表示最優目標值隨相應資源數量變化的變化率。

影子價格反映了不同的局部或個體的增量可以獲得不同的整體經濟效益。如果為了擴大生產能力，考慮增加設備，就應該從影子價格高的設備入手。這樣可以用較少的局部努力，獲得較大的整體效益。

三、對偶單純形法

1、基本思想

從原規劃的一個基本解出發，此基本解不一定可行，但它對應著一個對偶可行解（檢驗數非正），所以也可以說是從一個對偶可行解出發；然后檢驗原規劃的基本解是否可行，即是否有負的分量，如果有小于零的分量，則進行迭代，求另一個基本解，此基本解對應著另一個對偶可行解（檢驗數非正）。

如果得到的基本解的分量皆非負，則該基本解為最優解。也就是說，對偶單純形法在迭代過程中始終保持對偶解的可行性（即檢驗數非正），使原規劃的基本解由不可行逐步變為可行，當同時得到對偶規劃與原規劃的可行解時，便得到原規劃的最優解

什么情況下使用對偶單純性法呢？

在初始計算中 $\sigma^{T}=(-c^{T},0^{T})\leq0$ ，即對偶可行，但是由于 $-b\leq0$ ,所以 $\begin{cases}x_{s}=-b\leq0\\x=0\end{cases}$ ，所以原問題不可行。

應用前提：有一個基，其對應的基滿足:

（1）單純形表的檢驗數行全部非正（對偶可行）；

（2）變量取值可有負數（非可行解）。

注：通過矩陣行變換運算，使所有相應變量取值均為非負數即得到最優單純形表。

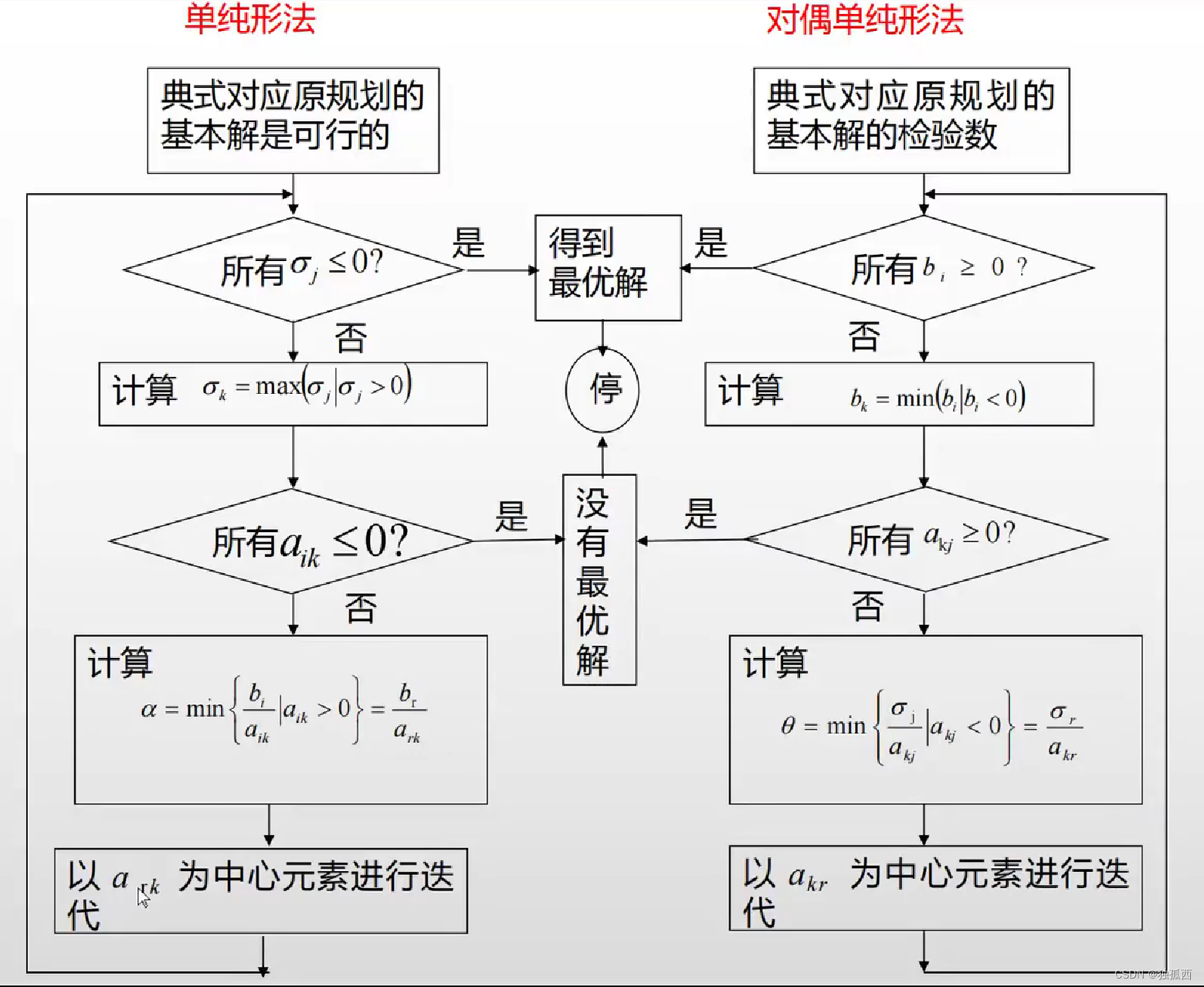
2、步驟

（1）建立初始對偶單純形表,對應一個基本解,所有檢驗數均非正,轉（2）。

（2）若 $b\geq 0$ ,則得到最優解,停止;否則,若有 $b_k<0$ 則選k行的基變量為出基變量,轉（3）。

（3）若所有 $a_{kj} \geq 0$ (j = 1,2,…,n)，則原問題無可行解,停止(因為以任何 $a_{kj}$ 為主元做主元消去時，都不可能使 $b_k$ 變為正數); 否則,若有 $a_{kj}<0$ 則選 $\theta=\min\{\sigma_{j}/a_{kj}|a_{kj}<0\}=\sigma_{r}/a_{kr}$ ，那么 $x_r$ 為進基變量,轉（4）。

（4）以 $a_{kr}$ 為主元,作矩陣行變換使其變為1,該列其他元變為0,利用主元消去計算A，b， $\sigma$ ，轉(2)。

$\theta$ 的選取保證新的檢驗數 $\sigma_j^{\prime}\leq0$ ,因為

$\sigma_j^{\prime}=\sigma_j-\frac{a_{kj}}{a_{kr}}\sigma_r=a_{kj}(\frac{\sigma_j}{a_{kj}}-\frac{\sigma_r}{a_{kr}})$

主元消去運算后，對偶問題的目標函數值減小（至少不增大），因為

$-(c_B^Tb)^{\prime}=-c_B^Tb-\frac{\sigma_r}{a_{kr}}b_k$

由于 $\frac{\sigma_r}{a_{kr}}b_k\leq0$ ，故 $-(c_B^Tb)'\geq-c_B^Tb$ ,即 $(c_B^Tb)'\leq c_B^Tb$

注：由于主元消去前 $a_{kj}$ 與 $b_k$ 同為負數，因此主元消去后右端列第k個分量變成正數，這有利于基本解向著滿足可行性的方向轉化。

3、例子

本文來自互聯網用戶投稿，該文觀點僅代表作者本人，不代表本站立場。本站僅提供信息存儲空間服務，不擁有所有權，不承擔相關法律責任。
如若轉載，請注明出處：http://www.pswp.cn/news/207081.shtml
繁體地址，請注明出處：http://hk.pswp.cn/news/207081.shtml
英文地址，請注明出處：http://en.pswp.cn/news/207081.shtml

如若內容造成侵權/違法違規/事實不符，請聯系多彩編程網進行投訴反饋email:809451989@qq.com，一經查實，立即刪除！