目錄
一、哈希表基礎?
二、哈希函數的設計
哈希函數的設計原則
三、java中的hashCode
基本數據類型的hashCode使用
自定義類型的hashCode使用?
需要注意
四、哈希沖突的處理 鏈地址法Seperate Chaining
五、實現屬于我們自己的哈希表
六、哈希表的動態空間處理和復雜度分析
七、哈希表更復雜的動態空間處理方法
我們哈希表的bug
八、更多哈希沖突的處理方法
開放地址法
其他
本篇博客花費大量時間寫的十分詳細,為了保證思路理解的連貫性,希望各位耐心地讀下去。
一、哈希表基礎?
參考LeetCode第387號問題:給定一個字符串,找到它的第一個不重復的字符,并返回它的索引。如果不存在,則返回 -1。
提示:你可以假定該字符串只包含小寫字母。
這種方法的時間復雜度是O(n)。

int[26] freq就是一個哈希表,每一個字符都和一個索引相對應,index = ch - 'a',這是哈希表的優勢——把字符轉化成一個索引。直接用一個數組來進行O(1)的查找操作,把字符轉化為索引的函數就稱為哈希函數f(ch) = ch - 'a'。
我們很難保證每一個鍵通過哈希函數的轉換會對應不同的索引,而兩個鍵對應同一個索引就會產生哈希沖突,我們需要在哈希表上操作來解決哈希沖突,這個我們后面再講。
哈希表完美的體現了用空間換時間的思想。比如我們18位數的身份證號的存儲,如果可用空間足夠大,我們可以用O(1)的時間實現。我們希望每一個鍵通過哈希函數得到的索引分布越均勻越好。
二、哈希函數的設計
學習哈希表我們最主要解決的兩個問題:一個是哈希函數的設計,一個是如何解決哈希沖突。
接下來我們來看各種類型的數據怎么通過哈希函數轉化為一個數組的索引。?
整型:
小范圍的正整數直接使用。
小范圍的負整數進行偏移。 -100 ~ 100 ——> 0 ~ 200
大整數:
比如18位的身份證號
方法:取模。? 比如取后四位,等同于mod10000,不能取后六位,因為牽扯到人的出生日期,一個月最多有31天,所以整個數據不會超過32萬,只利用32/100會造成分布不均勻。取后幾位還要考慮有沒有利用所有的信息,比如身份證號中還有人的出生省份、城市、月份等信息,如果不全面利用也會造成哈希沖突概率上升。一個簡單的解決辦法就是模一個素數。這個解決辦法的證明是數論的范疇,感興趣的朋友可以自己去了解一下。

由圖片我們可以看出,模一個素數比模一個和數分布更均勻。

?這個網站給出了根據數據規模不同,取什么素數是合適的。
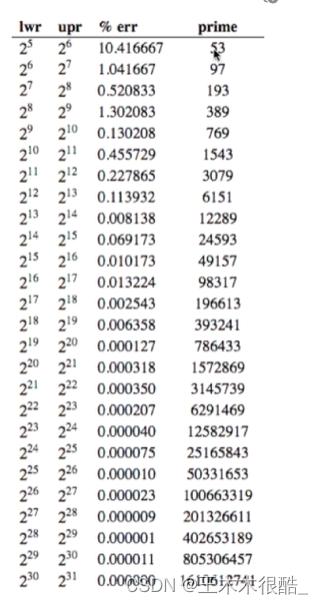
根據你的數據范圍,最后一列給出了推薦的素數。當然這種東西我們不需要深究,了解一下就好了。
浮點型:
在計算機中都是32或者64位的二進制表示,只不過計算機解析成了浮點數,如果我們的鍵是浮點型的話,我們就可以使用這個浮點型所存儲的空間當作整型來進行處理。也就是把浮點數所占用的32位或者64位的空間使用整數來進行解析,這片空間就同樣可以表示一個整數,問題就轉化成了一個大的整數來轉換成索引的方式。
字符串:
轉成整型處理,如果要區分字母大小寫,那么26進制還不夠,用戶自己可以選擇轉成多少進制的大整型。
下面這兩個式子是等價的,只是簡化了一些。M就是一個素數。
為了防止整型溢出,我們可以把取模挪到括號里面。
//為了實現字符串的這個小邏輯,我們寫個循環
int hash = 0;
for(int i = 0; i < s.length(); i++){hash = (hash * B + s.charAt(i)) % M}復合類型/自定義類型:
也是轉成整型類型,并且和字符串的處理方式差不多。
比如我們自定義一個日期類型——Date: year, month, day. 我們可以用字符串的方式來換成整型,如下式。
總而言之,我們都是轉成整型來處理,但這并不是唯一的方法,感興趣的朋友可以去了解更多。
哈希函數的設計原則

三、java中的hashCode
在java語言中,hashCode方法可以直接獲得基本數據類型的哈希函數的值,如果我們要自定義一個類型,我們可以覆蓋在Object類中就有的hashCode函數。
下面我們來看一下在java中hashCode的使用方法。
基本數據類型的hashCode使用
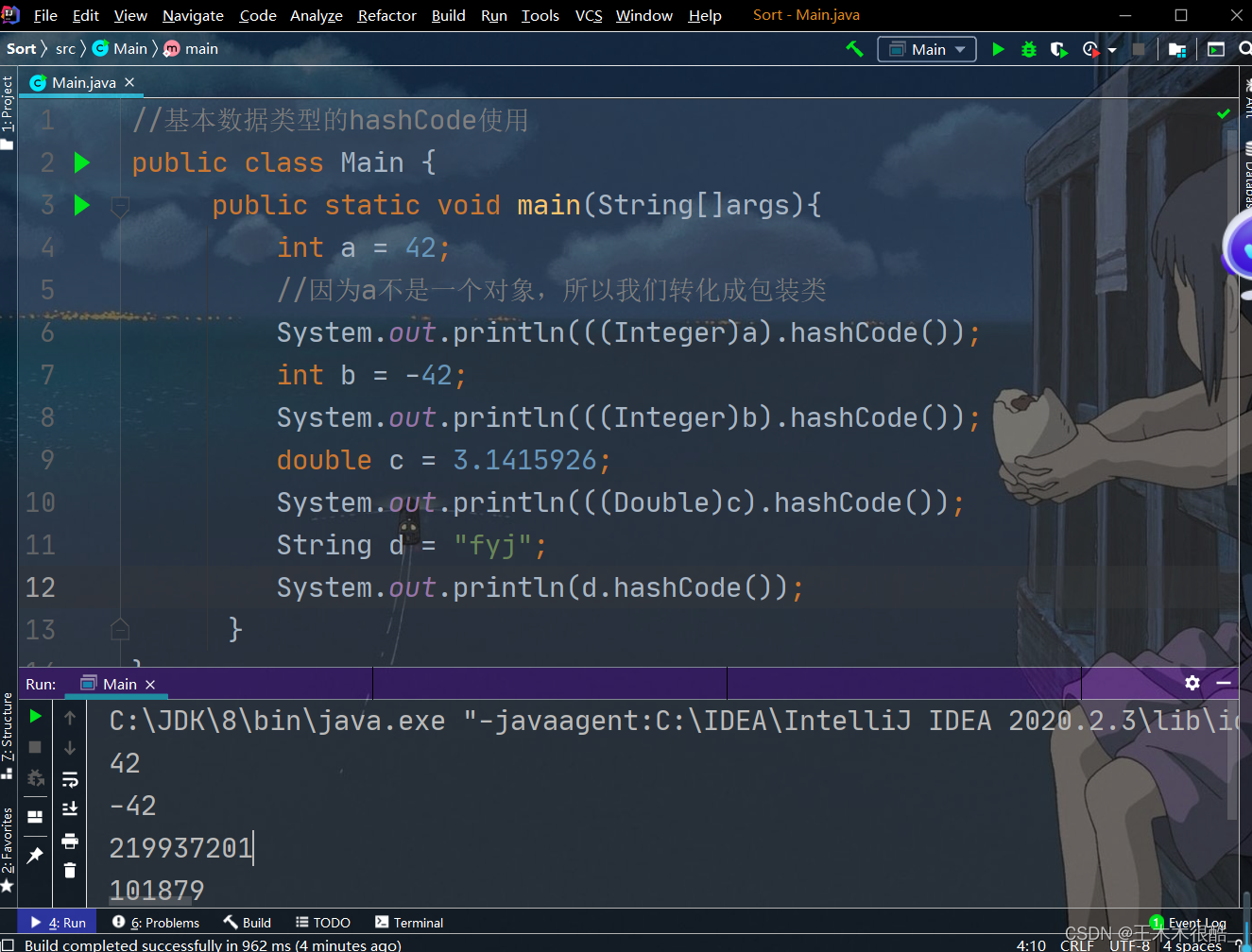
//基本數據類型的hashCode使用
public class Main {public static void main(String[]args){int a = 42;//因為a不是一個對象,所以我們轉化成包裝類System.out.println(((Integer)a).hashCode());int b = -42;System.out.println(((Integer)b).hashCode());double c = 3.1415926;System.out.println(((Double)c).hashCode());String d = "fyj";System.out.println(d.hashCode());}
}
自定義類型的hashCode使用?
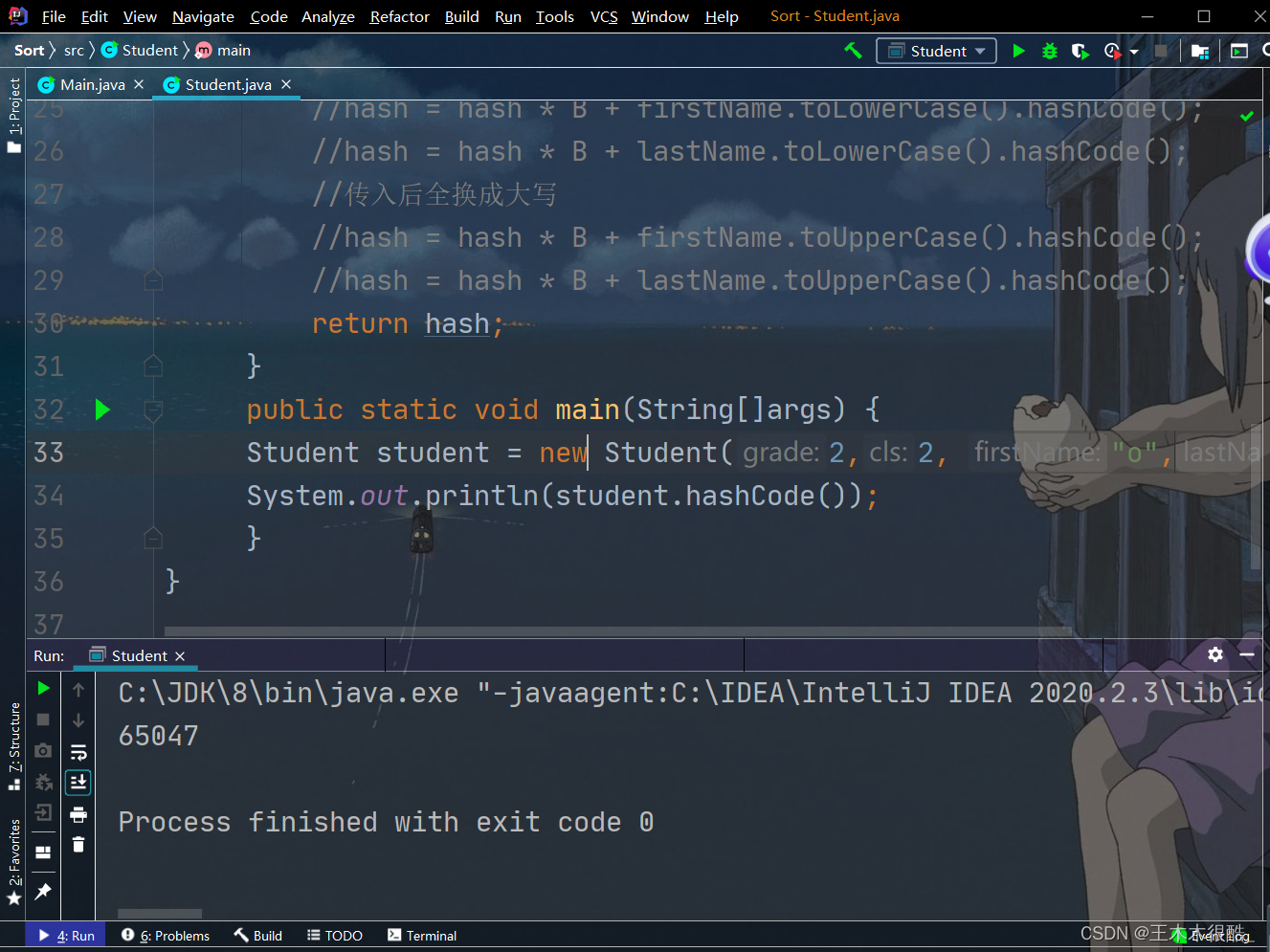
//自定義類型
public class Student {int grade;//年級int cls;//班String firstName;//名String lastName;//姓Student(int grade, int cls, String firstName, String lastName){this.grade = grade;this.cls = cls;this.firstName = firstName;this.lastName = lastName;}@Overridepublic int hashCode(){//把四部分看成四個數字,把整體看成這四部分組成的B這個進制的數int B = 31;int hash = 0;hash = hash * B + grade;hash = hash * B + cls;//firstName是字符串,我們可以調用它的hashCode轉化為一個整數hash = hash * B + firstName.hashCode();hash = hash * B + lastName.hashCode();//如果我們不希望區分大小寫,可以改成下面//傳入后全換成小寫//hash = hash * B + firstName.toLowerCase().hashCode();//hash = hash * B + lastName.toLowerCase().hashCode();//傳入后全換成大寫//hash = hash * B + firstName.toUpperCase().hashCode();//hash = hash * B + lastName.toUpperCase().hashCode();return hash;}public static void main(String[]args) {Student student = new Student(2,2, "o","f");System.out.println(student.hashCode());}
}
有了初步了解后,我們就可以嘗試著使用java中給我們提供的有關哈希表的數據結構,下面是java哈希表的基本使用方法。
//導入底層基于哈希表的集合HashSet
import java.util.HashSet;
import java.util.HashMap;
public class Main {public static void main(String[]args){Student student = new Student(2,2, "o","f");System.out.println(student.hashCode());HashSet<Student> set = new HashSet<>();set.add(student);HashMap<Student, Integer> scores = new HashMap<>();scores.put(student, 100);}
}
需要注意
如果我們自己覆蓋的那個HashCode方法注釋掉,我們再次運行依然可以成功。因為對于java來說,每一個Object類默認有一個HashCode的實現,它是根據我們創建的每一個Obect的地址相應的轉化成一個整型。如果我們在注釋掉自己覆蓋的HashCode情況下再創建一個student2,讓student2和student的內容一樣,運行出來的它們兩個的HashCode值是不一樣的。因為兩個對象的地址不同,轉化為的整型就不同。如果用我們自己覆蓋的HashCode方法,兩個HashCode值就一樣了。
我們自己覆蓋的HashCode方法只是幫助獲取對象的HashCode值,在產生哈希沖突的時候,我們依舊需要比較這兩個類是不是相等的。除了覆蓋HashCode,我們還需要equals來判斷兩個對象是否相等。
@Override//我們需要傳入的是Object類型,而不是Student類型public boolean equals(Object o){//是否是同一個引用if(this == o){return true;}if(o == null){return false;}//獲取對象的運行時類if(getClass() != o.getClass()){return false;}Student another = (Student)o;return this.grade == another.grade &&this. cls == another.cls &&this.firstName == another.firstName &&this.lastName == another.lastName;}這時候出現哈希沖突時,就算對應同一個值也可以區分出兩個對象。接下來我們將會真正實現一個哈希表。
四、哈希沖突的處理 鏈地址法Seperate Chaining
其實哈希表本質就是一個數組,我們先假設有這么一個數組,這時候來了一個鍵是k1的元素,我們只需要用hashcode(k1) % M,在java中hashcode相應的結果可能是負值,我們還要想辦法把負號給抹去。因為在Java中,哈希碼是一個int類型的值,可以是正數或負數。但是,哈希表中的索引值必須是非負整數,因此如果哈希碼是負數,就需要將其轉換為非負整數。
在看源碼或者別人寫的代碼中我們很常見到下面這種寫法:

通過整型和31個1按位與把最高位的負號抹去。因為計算機中二進制表示的最高位是符號位,1是負0是正,0和1按位與是0,1和1按位與還是0,最后都是正號。
假如k1計算完后索引為4,那么就存在數組索引為4的地方,這時候如果來了兩個索引都為2的k2、k3怎么辦?那我們就以鏈表的形式都存在索引為2的地方,這就是鏈地址法。
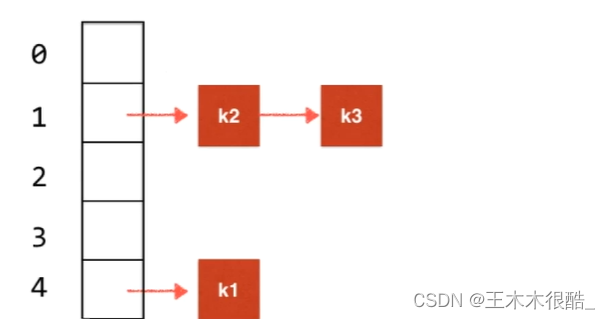
對于每個位置,我們說是存一個鏈表,其實它的本質就是存一個查找表, 查找表的實現方式還可以用樹結構實現,比如可以用平衡樹,這時候每個位置存的就不是一個鏈表,而是一個TreeMap的查找表,這時候我們的HashMap本質就是一個TreeMap的數組。

除了映射的角度,我們還可以從集合的角度,那時候HashSet 就是一個TreeSet數組。不管怎樣,哈希表的本質就是一個查找表,底層的數據結構只要是適合做查找表的就可以。

五、實現屬于我們自己的哈希表
//哈希表中的k不用像二分搜索樹一樣具有可比較性
//因此不用繼承Comparable接口
//同樣HashTable的k必須要實現hashCode這個方法
//不過在Java中所有的類型都是Object的子類,而Object默認實現了hashCode方法
//所以具體在代碼上我們對這個k也不需要有特殊的要求,如果有必要可以自己去覆蓋自己的hashCode方法//底層是一個紅黑樹
import java.util.TreeMap;public class HashTable<K, V> {private TreeMap<K, V>[] hashtable;private int size;//哈希表具體有多少個元素private int M; //哈希表有多少個位置/哈希表的大小public HashTable(int M){this.M = M;size = 0;hashtable = new TreeMap[M];//初始化數組for(int i = 0 ; i < M ; i ++)hashtable[i] = new TreeMap<>();//實例化}public HashTable(){this(97);//默認傳97的固定的值}private int hash(K key){//把key轉化成一個整型后通過按位與保證為非負數return (key.hashCode() & 0x7fffffff) % M;}public int getSize(){//哈希表中一共有多少元素return size;}public void add(K key, V value){//增TreeMap<K, V> map = hashtable[hash(key)];//基于多次重復計算的hash(key)小優化if(map.containsKey(key))//如果已存在key,那就理解成把key的值修改為valuemap.put(key, value);else{map.put(key, value);//真正的添加數據size ++;}}public V remove(K key){//刪V ret = null;//ret是return value的意思TreeMap<K, V> map = hashtable[hash(key)];//找到key對應的的哈希函數的值if(map.containsKey(key)){ret = map.remove(key);size --;}return ret;}public void set(K key, V value){//改TreeMap<K, V> map = hashtable[hash(key)];if(!map.containsKey(key))throw new IllegalArgumentException(key + " doesn't exist!");map.put(key, value);}public boolean contains(K key){//是否存在return hashtable[hash(key)].containsKey(key);}public V get(K key){//查詢某一個鍵對應的值是多少return hashtable[hash(key)].get(key);}
}六、哈希表的動態空間處理和復雜度分析
前面我們說過,我們創建的哈希表有M個地址,如果放入N個元素,那么平均來看每個地址會有N/M個元素會產生哈希沖突。?
如果每個地址是鏈表,那么時間復雜度O(N/M)。
如果每個地址是平衡樹,那么時間復雜度O(log(N/M))。
以上是平均來看的,而不是最壞的情況,最壞的情況是所有元素都擠在一個地址,那時候就分別是O(N)和O(logN)了。我們前面也說過哈希表的設計原則,我們的哈希表要盡可能地分布均勻。所以在哈希表設計恰當時是不會出現最壞情況的,我們還是要看平均情況下。
我們之前說哈希表的優勢在于能讓時間復雜度成為O(1)級別,現在我們的時間復雜度為什么都和N有關呢?原因就在于這個M是固定的,它是一個常數,當N趨于無窮大的時候,N/M總體也是趨于無窮的。?我們的哈希表就是一個數組,我們整體數據結構如果基于一個靜態數組是不合理的,空間總是固定的,所以我們的數組應該是動態內存分配的。當平均每個地址承載的元素多過一定程度時我們就擴容,反之就縮容。
下面是我們引入動態擴容縮容的哈希表代碼:
import java.util.Map;
import java.util.TreeMap;public class HashTable<K, V> {//設定平均每個地址哈希沖突的上界/下界private static final int upperTol = 10;private static final int lowerTol = 2;//初始容量private static final int initCapacity = 7;private TreeMap<K, V>[] hashtable;private int size;private int M;public HashTable(int M){this.M = M;size = 0;hashtable = new TreeMap[M];for(int i = 0 ; i < M ; i ++)hashtable[i] = new TreeMap<>();}public HashTable(){this(initCapacity);}private int hash(K key){return (key.hashCode() & 0x7fffffff) % M;}public int getSize(){return size;}public void add(K key, V value){TreeMap<K, V> map = hashtable[hash(key)];if(map.containsKey(key))map.put(key, value);else{map.put(key, value);size ++;//擴容if(size >= upperTol * M) //等價于size/M >= upperTolresize(2 * M);}}public V remove(K key){V ret = null;TreeMap<K, V> map = hashtable[hash(key)];if(map.containsKey(key)){ret = map.remove(key);size --;//縮容if(size < lowerTol * M && M / 2 >= initCapacity)//M不要小于初始的容積量resize(M / 2);}return ret;}public void set(K key, V value){TreeMap<K, V> map = hashtable[hash(key)];if(!map.containsKey(key))throw new IllegalArgumentException(key + " doesn't exist!");map.put(key, value);}public boolean contains(K key){return hashtable[hash(key)].containsKey(key);}public V get(K key){return hashtable[hash(key)].get(key);}//自動擴容實現private void resize(int newM){TreeMap<K, V>[] newHashTable = new TreeMap[newM];for(int i = 0 ; i < newM ; i ++)newHashTable[i] = new TreeMap<>();int oldM = M;this.M = newM;for(int i = 0 ; i < oldM ; i ++){TreeMap<K, V> map = hashtable[i];for(K key: map.keySet())newHashTable[hash(key)].put(key, map.get(key));}this.hashtable = newHashTable;}
}七、哈希表更復雜的動態空間處理方法
對于哈希表來說,元素從N增加到upperTol * N,地址空間增倍,均攤后的平均復雜度是O(1),每個操作在O(lowerTol) ~ O(upperTol)。
可能有細心的朋友會發現,當我們擴容M時,2 * M 不再是一個素數了,這樣可能會導致哈希表的分布不均勻。怎么解決呢?其實很簡單,我們可以根據前面提到的素數表來進行擴容。

比如,當我們初始的M是53,我們可以直接擴到下一個M推薦值97,而不是再用那種M * 2 的方式擴容了。觀察表我們可以發現,最后一列這些推薦的相鄰的素數值也在盡量地保持一個二倍左右的關系,這使擴容也更加合理。
下面是加入了素數表的哈希表代碼:
import java.util.TreeMap;public class HashTable<K extends Comparable<K>, V> {//素數表private final int[] capacity= {53, 97, 193, 389, 769, 1543, 3079, 6151, 12289, 24593,49157, 98317, 196613, 393241, 786433, 1572869, 3145739, 6291469,12582917, 25165843, 50331653, 100663319, 201326611, 402653189, 805306457, 1610612741};private static final int upperTol = 10;private static final int lowerTol = 2;private int capacityIndex = 0;//指向capacity數組的索引為0所在位置的數字private TreeMap<K, V>[] hashtable;private int size;private int M;public HashTable(){this.M = capacity[capacityIndex];size = 0;hashtable = new TreeMap[M];for(int i = 0 ; i < M ; i ++)hashtable[i] = new TreeMap<>();}private int hash(K key){return (key.hashCode() & 0x7fffffff) % M;}public int getSize(){return size;}public void add(K key, V value){TreeMap<K, V> map = hashtable[hash(key)];if(map.containsKey(key))map.put(key, value);else{map.put(key, value);size ++;if(size >= upperTol * M && capacityIndex + 1 < capacity.length){//防止數組越界capacityIndex ++;resize(capacity[capacityIndex]);}}}public V remove(K key){V ret = null;TreeMap<K, V> map = hashtable[hash(key)];if(map.containsKey(key)){ret = map.remove(key);size --;if(size < lowerTol * M && capacityIndex - 1 >= 0){capacityIndex --;resize(capacity[capacityIndex]);}}return ret;}public void set(K key, V value){TreeMap<K, V> map = hashtable[hash(key)];if(!map.containsKey(key))throw new IllegalArgumentException(key + " doesn't exist!");map.put(key, value);}public boolean contains(K key){return hashtable[hash(key)].containsKey(key);}public V get(K key){return hashtable[hash(key)].get(key);}private void resize(int newM){TreeMap<K, V>[] newHashTable = new TreeMap[newM];for(int i = 0 ; i < newM ; i ++)newHashTable[i] = new TreeMap<>();int oldM = M;this.M = newM;for(int i = 0 ; i < oldM ; i ++){TreeMap<K, V> map = hashtable[i];for(K key: map.keySet())newHashTable[hash(key)].put(key, map.get(key));}this.hashtable = newHashTable;}
}我們哈希表的均攤復雜度為O(1),同時我們犧牲了順序性。我們的算法難以避免的都是有得必有失的,有一種高級的數據結構是集合和映射,現在我們要有意識的把它分為基于平衡樹的有序集合和有序映射以及基于哈希表的無序集合和無序映射。希望感興趣的朋友可以嘗試自己封裝屬于自己的無序集合和無序映射。
我們哈希表的bug
我們前面代碼中提到我們的HashTable中的K是不需要具有可比較性的,這是哈希表的一個優點,同時我們也失去了哈希表的順序性。但是我們的實現的TreeMap的k是需要繼承Comparable具有可比較性的,這時K產生了矛盾,這是一個bug。

如果我們的每個地址對應一個鏈表 ,那么這個矛盾是不存在的,畢竟鏈表不需要有可比較性。我們前面提到的哈希沖突達到一定程度會轉成紅黑樹,其實這種轉換也是有條件的,前提就是實現了可比較性,不然就仍然保持鏈表,這樣就保證了我們的代碼是有邏輯的。

八、更多哈希沖突的處理方法
開放地址法
定義:對于我們哈希表中的每一個地址,所有的哈希值的元素都有可能進來。?每一個地址不再是存儲鏈表了,而是直接存儲元素的值,如果有兩個元素產生了哈希沖突,那么第二個元素就放在第一個元素往后找下一個空的地方,如下圖所示。

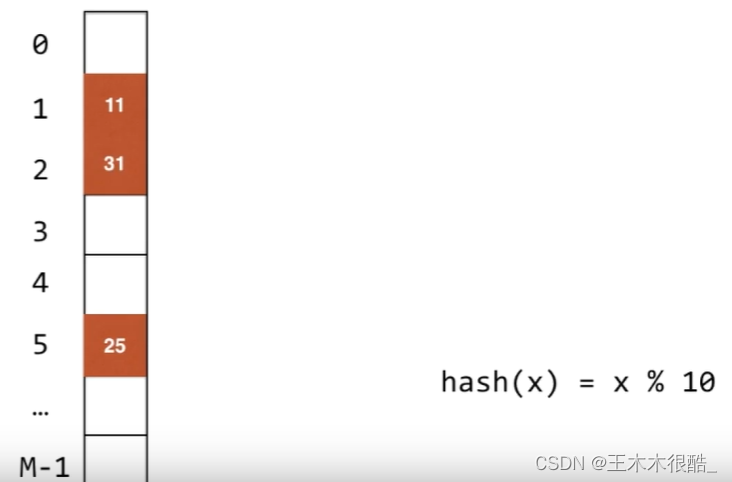

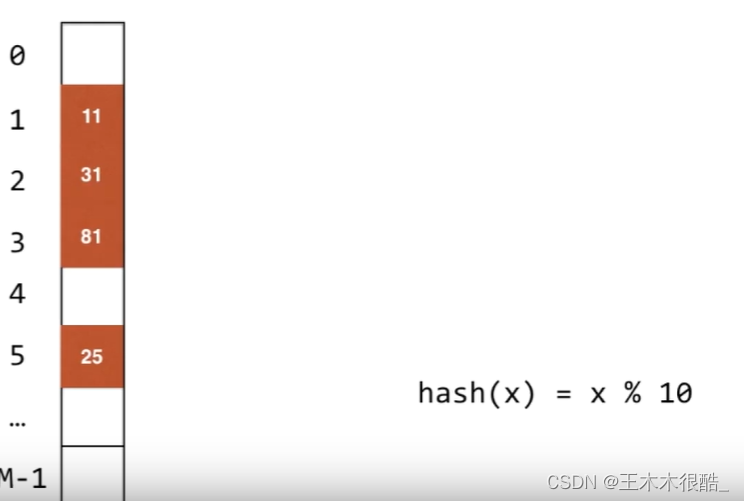
這種方法在某些情況下效率是很低的,比如如果一塊很大的連續空間已經被占滿了,這時又來了一個元素需要放在索引為1的位置,這時候它就需要從頭開始一直往下找空的位置。我們對此的解決方法是不再每次只走一個位置了,而是使用平方探測法,遇到哈希沖突時依次+1 +4 +9 +16來尋找空的地址。我們也可以用二次哈希法,遇到哈希沖突時我們用另一個哈希函數來計算它要存放的地址。
對于開放地址法,我們也可以設計擴容操作,只要擴容的負載率的值選的合適,那么時間復雜度也可以是O(1)級別的。
其他
除了鏈地址法和開放地址法這兩個有名的方法,還有再哈希法Rehashing、Coalesced Hashing,感興趣的朋友可以自己去了解。?


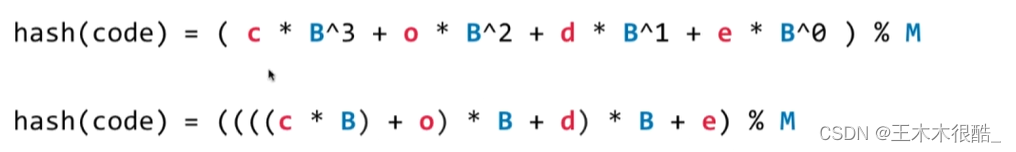



)










覆蓋優化 - 附代碼)




)

