1、聚類概述

聚類（Clustering）是指將不同的對象劃分成由多個對象組成的多個類的過程，由聚類產生的數據分組，同一組內的對象具有相似性，不同組的對象具有相異性，它是一類機器學習基礎算法的總稱，聚類的核心計算過程是將數據對象集合按相似程度劃分成多個類，劃分得到的每個類稱聚類的簇。
簇（Cluster）是由距離鄰近的對象組合而成的集合。聚類的最終目標是獲得緊湊、獨立的簇集合。一般采用相似度作為聚類的依據，兩個對象的距離越近，其相似度就越大。
由于聚類時待劃分的類別未知，即訓練數據沒有標簽，因此聚類的準確率相對于分類而言較低一點，但是聚類最大的特點是可以發現新知識、新規律，因此，聚類也是了解未知世界的一種重要手段。聚類可以單獨實現，通過劃分尋找數據內在分布規律，也可以作其他學習任務的前驅過程。
由于聚類使用的數據是無標記的，因此聚類屬于非監督學習。聚類本質上仍然是對數據類別進行劃分的問題，但是由于沒有固定的類別標準，因此聚類的核心問題是如何定義簇。最常用的方法是依據樣本間距離、樣本的空間分布密度等來確定。按照簇的定義和聚類的方式，聚類大致分為以下幾種：K-Means 為代表的簇中心聚類、基于連通性的層次聚類、以EM算法為代表的概率分布聚類、以 DBSCAN 為代表的基于網格密度的聚類，以及高斯混合聚類等。

2、K-Means聚類算法原理

K-Means 聚類算法也稱為K均值聚類算法，是典型的聚類算法。對于給定的數據集和需要劃分的類數k，算法根據距離函數進行迭代處理，動態地把數據劃分成k個簇（即類別），直到收斂為止。簇中心也稱為聚類中心。
K-Means 聚類的優點是算法簡單、運算速度快，即便數據集很大計算起來也較便捷。不足之處是如果數據集較大，容易獲得局部最優的分類結果，而且所產生的類的大小相近，對噪聲數據也比較敏感。
K-Means 算法的實現過程較為簡單，首先選取k個數據點作為初始的簇中心，即聚類中心。初始的聚類中心也被稱作種子。然后，逐個計算各數據點到各個聚類中心的距離，把數據點分配到離它最近的簇。一次選代之后，所有的數據點都會分配給某個簇。再根據分配結果計算出新的聚類中心，并重新計算各數據點到各種子的距離，根據距離重新進行分配。不斷重復計算和重新分配的步驟，直到分配不再發生變化或滿足終止條件為止。
算法的整體流程如下：

隨機選擇k個點作為聚類中心
while 不滿足終止條件：for 數據集中的每個數據點：for k個聚類中心：計算每個點到每個聚類中心的距離比較滯后將數據點分配到最近的聚類中心for 每個簇：對聚類中心進行更新，更新為簇內所有點的均值

在上述過程中，終止條件一般可以設置為循環次數或者較小的誤差值等。

由于聚類對劃分的類別沒有固定的定義，因此也沒有固定的評價指標，一般來說聚類算法的理想目標是類內距離最小，類間的距離最大，因此，通常依此目標建立K-Means 聚類的目標函數。
假設數據集X包含n個數據點，需要劃分到k個類。聚類中心用集合U表示。聚類后所有數據點到各自聚類中心的差的平方和為聚類平方和，用J表示，則J值的計算過程如下：

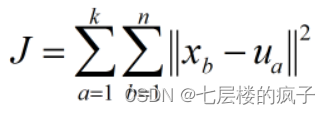
聚類的目標就是使J值最小化，如果在多次迭代之后，J值不再發生變化，說明簇的分配不再發生變化，算法已經收斂。另外計算每個點到聚類中心的距離一般采用歐氏距離進行計算。

3、K-Means聚類實現

3.1 基于SKlearn實現K-Means聚類

SKlearn的cluster模塊中提供的KMeans類可以幫助實現K-means聚類，其語法格式如下：

sklearn.cluster.KMeans(n_clusters=8,init='k-means++',n_init=10,max_iter=300,tol=0.0001,precompute_distances='auto',verbose=0,random_state=None,copy_x=True,n_jobs=None,algorithm='auto')

在上述格式中，n_clusters表示要形成的簇的數目，即類的數量，為可選項，默認為8；init用于接收待定的string，k-means++表示該初始化策略選擇的初始均值向量之間都距離比較遠，它的效果較好；n_init表示用不同種子運行K-Means 算法的次數，默認為10；max_iter表示單次運行的K-Means 算法的最大迭代次數，默認300；tol表示算法收斂的閾值；precompute_distances可選參數為Boolean或auto，表示是否提前計算好樣本之間的距離；verbose表示是否輸出日志信息，取值為0時表示不輸出，取值越大，打印次數越頻繁；random_state表示隨機數生成器的種子；copy_x表示在進行距離計算前，是否要將數據居中以提高計算準確性，True表示不修改數據；n_jobs表示任務使用的CPU數量；algorithm表示對K-Means經典算法的選擇。

返回KMeans 対象的屬性主要有：
cluster_centers_：數組類型，各個簇中心的坐標。
labels_：每個數據點的標簽。
inertia_：浮點型，數據樣本到它們最接近的聚類中心的距腐平方和。
n_iter_：運行的選代改數。

KMeans類主要提供三個方法，功能及語法格式分別如下：
fit方法用于進行K-means聚類計算。

fit(X[,y,sample_weight])

predict方法用于預測X中的每個樣本所屬的最近簇。

predict(X[,sample_weight])

fit_predict用于計算簇中心，并預測每個樣本的所屬簇。

fit_predict(X[,y,sample_weight])

例：對sklearn中提供的鳶尾花數據集進行聚類。

from sklearn import datasets
from sklearn.cluster import KMeans
iris = datasets.load_iris()    #數據導入
X = iris.data    #將特征數據作為聚類數據
y = iris.target   #保留標簽
clf=KMeans(n_clusters=3)    #設置類別為3的聚類器
model=clf.fit(X)    #訓練模型
predicted=model.predict(X)    #預測每個樣本所屬的類別
#將預測值與標簽真值進行對比
print('the predicted result:\n',predicted)
print("the real answer:\n",y)

3.2 自編寫方式實現K-Means聚類

除了使用SKlearn的cluster模塊來實現K-Means聚類外，還可以根據實際問題采用自編寫的方式來實現K-Means聚類。
例：假設某物流公司要給城市的50個客戶配送貨物。假設公司只有5輛貨車，客戶的地理坐標在testSet.txt文件中，如何進行車輛分配使得配送效率最高？
問題分析：可以使用K-Means 算法，將文件內的地址數據聚成5類，由于每類的各戶地址相近，則可以分配給同一輛貨車。

from numpy import *
from matplotlib import pyplot as plt    
#計算兩個向量的歐式距離
def distEclud(vecA, vecB):return sqrt(sum(power(vecA - vecB, 2)))
#選K個點作為初始中心點   
def initCenter(dataSet, k):print('2.初始化中心點...')shape=dataSet.shapen = shape[1]  #數據集列數    classCenter = array(zeros((k,n)))  #數組保存中心點信息，k行n列#取數據集中前k個數據點作為初始聚類中心for j in range(n):        firstK=dataSet[:k,j]classCenter[:,j] = firstKreturn classCenter#實現K-Means算法   
def myKMeans(dataSet,k):m = len(dataSet)                 #數據集行數，即樣本點個數    clusterPoints = array(zeros((m,2)))   #使用clusterPoints保存數據點所屬的簇序號以及距離，預設為（0，0）classCenter = initCenter(dataSet, k)  #調用initCenter函數進行各簇中心初始化clusterChanged = True  #用True和False表示是否要重新執行聚類的過程print('3.數據點距離計算以及簇的分配...')while clusterChanged:     #重復計算，直到簇分配不再變化clusterChanged = False#將每個數據點分配到最近的簇for i in range(m):   minDist = inf  #首先定義一個無窮大的值作為最近距離minIndex = -1  #預設最近的簇的序號為-1for j in range(k):distJI = distEclud(classCenter[j,:],dataSet[i,:])if distJI < minDist:  #如果樣本點到某個簇的距離小于minDist，則將最近距離minDist以及所屬簇的序號進行替換minDist = distJI; minIndex = jif clusterPoints[i,0] != minIndex:  #如果第i個點所屬的簇序號發生了改變clusterChanged = True  #取值為True，表示要重新進行距離計算以及簇的分配，只有當所有點的簇序號不再更新時，則不在執行此過程clusterPoints[i,:] = minIndex,minDist**2  #對每個點所屬的的簇序號以及距離進行更新#重新計算簇中心   for cent in range(k):#nonzero獲得數據中滿足條件的的元素位置下標并返回一個數組，[0]表示將數據行數單獨提取出來，ptsInClust即保存了屬于每個簇的數據ptsInClust = dataSet[nonzero(clusterPoints[:,0]==cent)[0]]  classCenter[cent,:] = mean(ptsInClust, axis=0)return classCenter, clusterPoints
#顯示聚類結果    
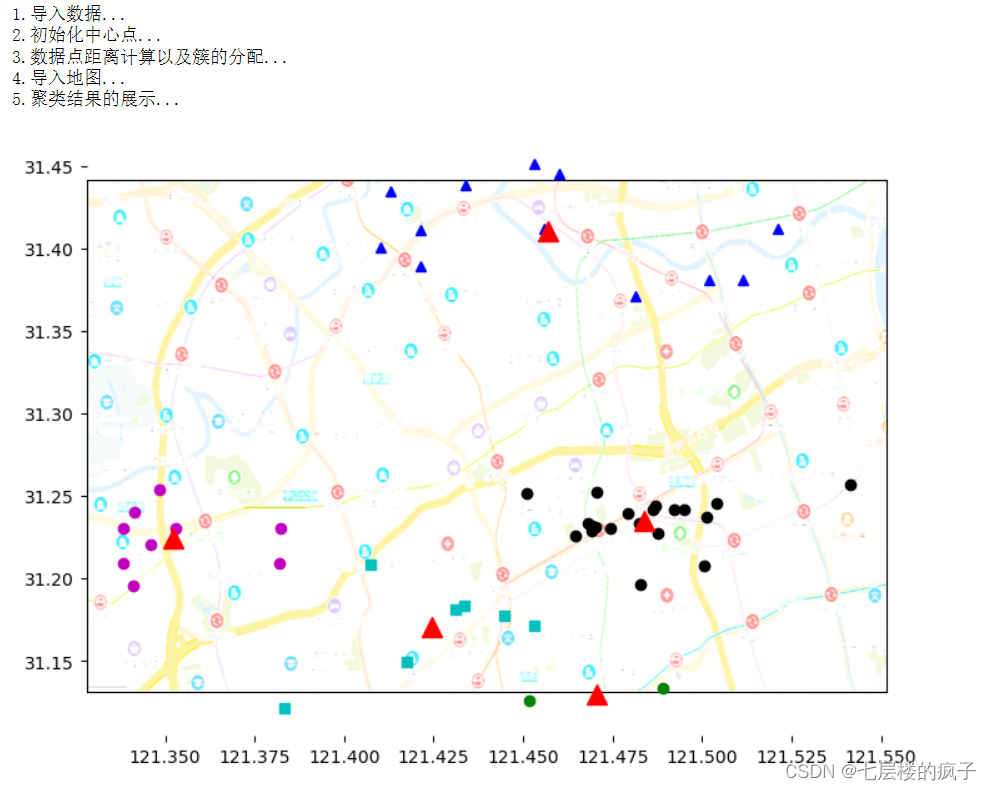
def show(dataSet, k, classCenter, clusterPoints):   print('4.導入地圖...')fig = plt.figure()#定義添加到圖片中子區域的左下角坐標，寬度、高度rect=[0.1,0.1,1.0,1.0]axprops = dict(xticks=[], yticks=[])ax0=fig.add_axes(rect, label='ax0', **axprops)  #axprops用于接收刻度值imgP = plt.imread('city.png')#在相同區域添加axes，后面添加的axes會把前面添加的axes覆蓋ax0.imshow(imgP)ax1=fig.add_axes(rect, label='ax1', frameon=False)  #frameon=False表示不顯示邊框print('5.聚類結果的展示...')numSamples = len(dataSet)   #對象數量mark = ['ok', '^b', 'om', 'og', 'sc']  #根據每個對象的坐標繪制點for i in range(numSamples): #因此保存的所屬簇的序號不是正整數，所以先對標簽進行轉換markIndex = int(clusterPoints[i, 0])%k  ax1.plot(dataSet[i, 0], dataSet[i, 1], mark[markIndex])  #標記每個簇的中心點    for i in range(k):  markIndex = int(clusterPoints[i, 0])%k         ax1.plot(classCenter[i, 0], classCenter[i, 1], '^r', markersize = 12)  plt.show()print('1.導入數據...')
dataSet=loadtxt('testSet.txt')
K=5   #類的數量
classCenter,classPoints= myKMeans(dataSet,K)
show(dataSet,K,classCenter,classPoints)

4、算法不足與解決思路

K-Means算法過程簡單，實現便捷，但是該算法也存在一定的問題。

4.1 存在的問題

1、k值較難確定
大多時候并不知道數據集應該分成多少類。實際使用時，類的數量可以是經驗值，也可以多次處理選取其中最優的值，或者通過類的合并或分裂得到。
2、初始聚類中心的選擇對聚類結果有較大影響
例如剛剛采用自編寫方式實現K-Means聚類的例子中，初始聚類中心選擇的是前k個，如果將初始聚類中心修改為中間k個、后k個或者任意的k個值，所得到的結果是不同的。也就是說，初始值選擇的好壞是關鍵性的因素，這也是K-Means 算法的一個主要問題。
3、K-Means 算法的時間開銷比較大
由于算法需要重復進行計算和樣本歸類，又反復調整聚類中心，因此算法的時間復雜度較高。尤其當數據集比較大時，將耗費很多時間。
4、K-Means 算法的功能具有局限性
由于算法是基于距離進行分配的，當數據包含明確分開的幾部分時，可以良好地劃分，然而，如果數據集形狀較為復雜，比如是相互存在環繞的數據集，K-Means算法就難以處理了。

4.2 常見K值確定方法

前面存在的問題主要還是存在k值的確定上，目前研究人員提出了許多確定k值的方法，常見的幾種方法如下：
1、經驗值
在實際問題中，大部分的樣本都只會被劃分成數量較少、明確的類別，因此很多時候人們會根據經驗來確定k值。
2、觀測值
在聚類之前，可以用繪圖方法將數據集可視化，然后通過觀察，人工決定將樣本聚成幾類。
3、肘部方法
肘部方法（Elbow Method）是將不同的模型參數與得到的結果可視化，例如擬合出折線，幫助數據分析人員選擇最佳參數。
如果不同的參數對算法結果有影響，則折線圖會發生變化。例如，折線圖會出現拐點，類似于手臂上的“肘部”，則表示拐點位置為模型參數的關鍵。
4、性能指標法
通過性能指標來確定k值，例如，選取能使輪廓系數（聚類評估的方法，值越大聚類效果越好）最大的k值。

4.3 算法評估優化思路

為了進一步提高聚類效果，可以在聚類之后再進行后期處理。例如，可以對聚類結果進行評估，根據評估進行類的劃分或合并。
評價聚類算法可以使用誤差值，常用的評價聚類效果的指標是誤差平方和SSE。SSE 的計算比較簡單，統計每個點到所屬的簇中心的距離的平方和。假設n代表該簇內的數據點的個數，y’表示該簇數據點的平均值，簇的誤差平方和SSE 的計算公式如下：

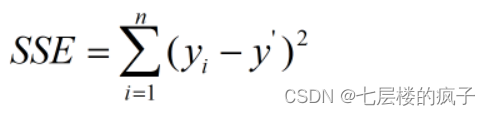
SSE值越小，表明該簇的離散程度越低，聚類效果越好。可以根據SSE值對生成的簇進行后處理，例如，將SSE值偏大的簇進行再次劃分。
在K-Means算法中，由于算法收斂到局部最優，因此不同的初始值會產生不同的聚類結果。針對這個問題，使用誤差值進行后處理后，離散程度高的類被拆分，得到的聚類結果更為理想。
除了在聚類之后進行處理，也可以在聚類的主過程中使用誤差進行簇劃分，比如常用的二分 K-Means 聚類算法。
二分K-Means 聚類的思路是首先將所有數據點看作一個簇，然后將該簇一分為二，計算每個簇內的誤差指標（如SSE值），將誤差最大的簇再劃分成兩個簇，降低聚類誤差，之后不斷重復進行，直到簇的個數等于用戶指定的k值為止。由此思路可以看出，二分K-Means算法能夠在一定程度上解決K-Means收斂于局部最優的問題。

自編寫方式實現K-Means聚類物流配送問題源碼及數據集