【數據結構】—搜索二叉樹（C++實現，超詳細！）

?? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ???????????????🎬慕斯主頁：修仙—別有洞天

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?????????????????? ??今日夜電波：消えてしまいそうです—真夜中

? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 1:15━━━━━━?💟──────── 4:18
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ????🔄 ? ?? ? ? ? ?? ? ????

??????????????????????????????????????💗關注👍點贊🙌收藏您的每一次鼓勵都是對我莫大的支持😍

一、二叉搜索樹概念

? ? ? ? 什么是二叉搜索樹？?

? ? ? ??二叉搜索樹的基本操作

二、二叉搜索樹的實現

? ? ? ? ?節點的定義

? ? ? ? ?二叉搜索樹的定義

非遞歸操作

? ? ? ? 插入操作

? ? ? ? 查找操作?

? ? ? ? 刪除操作（重點及難點！！！）

遞歸法操作?

? ? ? ? 中序遍歷排升序（經典操作！）?

? ? ? ? ?插入操作（遞歸）

? ? ? ? ?查找操作（遞歸）

? ? ? ? 刪除操作（遞歸）?

?二叉搜索樹的應用

? ? ? ??KV模型二叉搜索樹

三、整體代碼?

一、二叉搜索樹概念

? ? ? ? 什么是二叉搜索樹？?

二叉搜索樹（Binary Search Tree，BST）是一種特殊的二叉樹，它滿足以下幾個條件：

左子樹中所有節點的值小于當前節點的值。
右子樹中所有節點的值大于當前節點的值。
左子樹和右子樹也都是二叉搜索樹。

????????二叉搜索樹的中序遍歷可以得到一個升序的序列，因此它常被用來實現有序集合或映射。在二叉搜索樹中，查找、插入和刪除操作的時間復雜度通常為O(logn)，其中n為樹中節點的數量，這得益于二叉搜索樹的結構和查找方法。

? ? ? ? ?如下便是一顆二叉搜索樹：

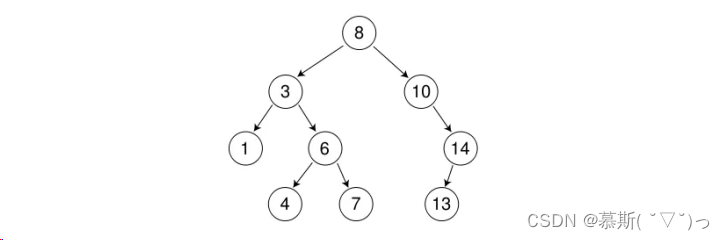
? ? ? ? 一句話總結二叉搜索樹：

????????????????左子樹節點總是比父節點小，右子樹節點總是比父節點大的二叉樹。

? ? ? ??二叉搜索樹的基本操作

? ? ? ? ?利用二叉搜索樹特性排升序。一聽到二叉樹，我們通常會想到的是什么？遞歸！請細細想想我們二叉搜索樹的特點->左邊的節點總是比父節點小，右邊的節點總是比父節點大！那么我們對它使用中序遍歷會發生什么呢？還是上面的那顆二叉樹，對他進行中序遍歷后：

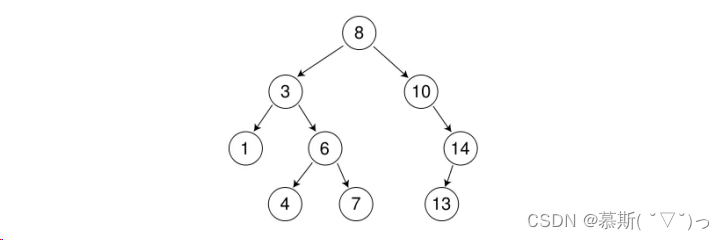
? ? ? ? 中序遍歷結果：arr={1,3,4,6,7,8,10,13,14};

二、二叉搜索樹的實現

? ? ? ? ?節點的定義

? ? ? ? ? 說來慚愧作者在此前實現數據結構都是用C語言實現的?o (╥﹏╥)o.?，本文應該是作為作者第一篇用C++實現的數據結構，也算是一個新的起點吧！

? ? ? ? 與C語言的區別主要還是在于在此使用struct（實際上是類）可以在定義時就進行初始化，利用的就是類的初始化列表的作用，這就省去了我們C語言時需要額外定義以及調用的初始化操作。只能說有了C++，C語言什么的不認識啦?（′???）?

	//節點定義template<class K>struct BSTreeNode{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}};

? ? ? ? ?二叉搜索樹的定義

? ? ? ? ?對于節點實例化并且重命名，并且給數據進行缺省賦值。

	//二叉搜索樹template<class K>class BSTree{typedef BSTreeNode<K> Node;public://...諸多的操作private:Node* _root = nullptr;};

非遞歸操作

? ? ? ? 插入操作

????????插入的具體過程如下：

????????a. 樹為空，則直接新增節點，賦值給root指針

????????b. 樹不空，按二叉搜索樹性質查找插入位置，插入新節點

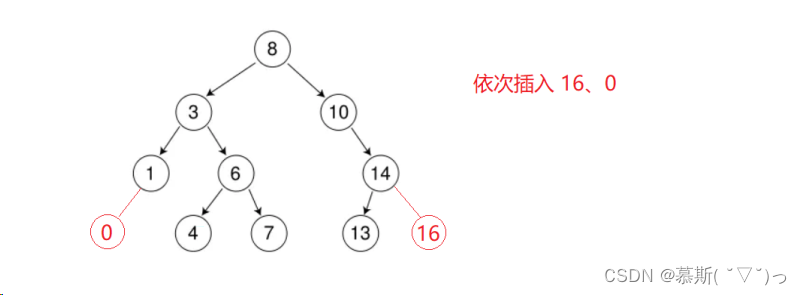
? ? ? ? ?思路：判斷是否為空->是-》直接給根節點賦值->否->進行循環遍歷對要插入的值進行“比大小”->大往右，小往左遍歷，直到空為止->比較空位置父節點的大小，大插右，小插左

		//插入操作，按照左小右大的規則bool Insert(const K& key){if (_root == nullptr){_root = new Node(key);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){parent = cur;if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return false;}}cur = new Node(key);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}

? ? ? ? 查找操作?

? ? ? ? 通過搜索二叉樹的特性，通過比較大小即可完成查找。

		//查找操作bool Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return true;}}return false;}

? ? ? ? 刪除操作（重點及難點！！！）

?????????首先查找元素是否在二叉搜索樹中，如果不存在，則返回, 否則要刪除的結點可能分下面四種情況：

????????a. 要刪除的結點無孩子結點

????????b. 要刪除的結點只有左孩子結點

????????c. 要刪除的結點只有右孩子結點

????????d. 要刪除的結點有左、右孩子結點

????????看起來有待刪除節點有4中情況，實際情況a可以與情況b或者c合并起來，因此真正的刪除過程如下：

????????情況b：刪除該結點且使被刪除節點的雙親結點指向被刪除節點的左孩子結點--直接刪除

????????情況c：刪除該結點且使被刪除節點的雙親結點指向被刪除結點的右孩子結點--直接刪除

????????情況d：在它的右子樹中尋找中序下的第一個結點(關鍵碼最小)，用它的值填補到被刪除節點中，再來處理該結點的刪除問題--替換法刪除

? ? ? ? 而在b、c、d這三種情況中，b和c又很相似，所以以大類來劃分，我們實際可以分為兩種。一種是要刪除的節點只有一個左孩子或者右孩子，另一種是有兩個孩子節點。

? ? ? ? ?現在詳細介紹這兩種情況：

? ? ? ? 當只有一個孩子節點時：當要刪節點的左孩子為空時，我們只需要將右半邊給他的父親就行，當然我們也需要注意以下兩點：1、如果要刪節點是根節點，那么我們需要將它的右孩子的地址覆蓋原節點。2、要刪節點不是根節點，那么我們也需要判斷要刪節點是它父節點的左孩子還是右孩子；左孩子則父節點的左孩子節點指向要刪孩子的右孩子，右孩子則父節點的右孩子節點指向要刪孩子的右孩子。當要刪右孩子時也是同理，只是需要注意此時要注意的第二點中要指向的是要刪節點是右孩子。下面上半部分的圖為此部分的圖解~

? ? ? ? ? 當有兩個孩子節點時：我們則需要用到替換法。首先，我們需要根據以下規則中的一個規則：1、找到要刪節點的左子樹的最大節點。2、找到要刪奇點的右子樹的最小節點。接著，交換要刪節點和找到的這個節點。最后，刪除找到節點的位置，這個時候，我們就需要返回到上一部分我們只有一個孩子節點時要走的步驟，進行相應的操作。為什么呢？因為我們都知道要找最小或者最大只有在最左或者最右。而此時我們一定滿足只有一個孩子節點時的于要求。下面下半部分的圖為此部分的圖解，這里取右子樹的最小~

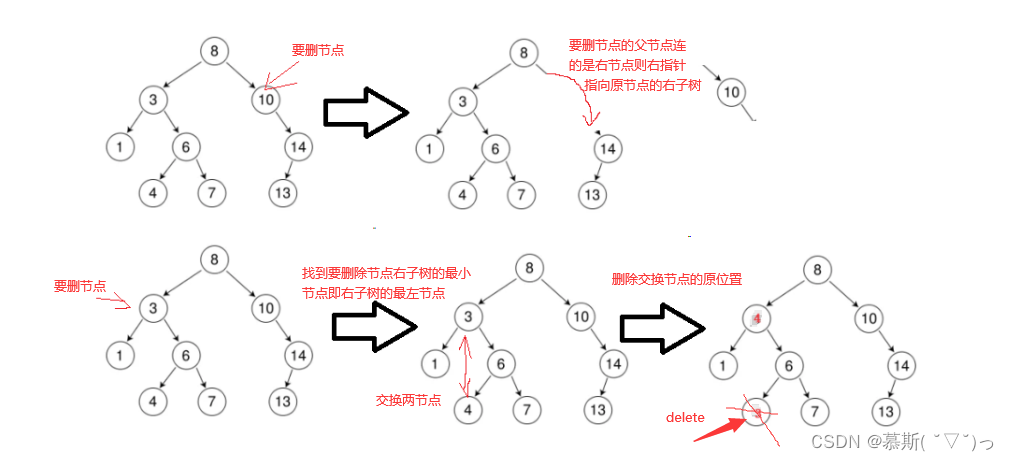
? ? ? ? 實現如下：?

		bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else//表示已經找到，進行刪除操作{//左為空的情況if (cur->_left == nullptr){if (cur == _root)//要刪即為根節點{_root = cur->_right;}else{if (cur == parent->_left)//因為左一定為空，為父節點的左則將右半邊給父即可{parent->_left = cur->_right;}else//同理為父節點的右則將右半邊給父{parent->_right = cur->_right;}}delete cur;}else if (cur->_right == nullptr)//右為空的情況{//同理左為空if (cur == _root){_root = cur->_left;}else{if (cur == parent->_left){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;}else//左右都不為空{//可以選擇找該節點左子樹的最大節點（最右節點）或者右子樹的最小節點（最左節點）//這里找右樹的最小節點(最左節點)Node* parent = cur;Node* subleft = cur->_right;while (subleft->_left){parent = subleft;subleft = subleft->_left;}swap(cur->_key, subleft->_key);//由于找到的是最左，則默認左為空,所以只需將右鏈接給父節點if (subleft == parent->_left){parent->_left = subleft->_right;}else{parent->_right = subleft->_right;}delete subleft;}return true;}}return false;}

????????

遞歸法操作?

? ? ? ? 中序遍歷排升序（經典操作！）?

? ? ? ? 上面詳細介紹過了，不多闡述~

		void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}

? ? ? ? ?插入操作（遞歸）

? ? ? ? 實際上同非遞歸的原理是相同的，不多闡述。實在不行畫遞歸展開圖就理解了~

		bool _InsertR(Node*& root, const K& key){if (root == nullptr){root = new Node(key);return true;}if (root->_key < key)return _InsertR(root->_right, key);else if (root->_key > key)return _InsertR(root->_left, key);elsereturn false;}

? ? ? ? ?查找操作（遞歸）

		bool _FindR(Node* root, const K& key){if (root == nullptr){return false;}if (root->_key < key){return _FindR(root->_right, key);}else if (root->_key > key){return _FindR(root->_left, key);}else{return true;}}

? ? ? ? 刪除操作（遞歸）?

? ? ? ? 實際上操作同非遞歸是一致的?，特別注意接口的對于root的引用，這對于后續刪除很有作用。當要刪除只有一個孩子節點的節點時，同非遞歸的思想是一樣的。當要刪節點有兩個孩子節點時，在最后面采取的是裝換成在子樹中去刪除，同非遞歸中的找到替換節點轉到只有一個孩子的操作是一樣的思想。

		bool _EraseR(Node*& root, const K& key){if (root == nullptr)return false;if (root->_key < key){return _EraseR(root->_right, key);}else if (root->_key > key){return _EraseR(root->_left, key);}else//找到了開始刪除{//實際上的操作同非遞歸差不多，這里巧妙的對root運用了引用if (root->_left == nullptr){Node* del = root;root = root->_right;delete del;return true;}else if (root->_right == nullptr){Node* del = root;root = root->_left;delete del;return true;}else//找右子樹的最大{Node* subleft = root->_right;while (subleft->_left){subleft = subleft->_left;}swap(root->_key, subleft->_key);// 轉換成在子樹去遞歸刪除return _EraseR(root->_right, key);}}}

?二叉搜索樹的應用

? ? ? ? 以上我們實現的二叉搜索樹實際上也被稱為K模型，而實際上還有一種模型叫做KV模型，以下為詳細介紹：
?????????1. K模型：K模型即只有key作為關鍵碼，結構中只需要存儲Key即可，關鍵碼即為需要搜索到的值。比如：

????????給一個單詞word，判斷該單詞是否拼寫正確，具體方式如下：

????????以詞庫中所有單詞集合中的每個單詞作為key，構建一棵二叉搜索樹

????????在二叉搜索樹中檢索該單詞是否存在，存在則拼寫正確，不存在則拼寫錯誤。

????????2. KV模型：每一個關鍵碼key，都有與之對應的值Value，即<Key, Value>的鍵值對。該種方式在現實生活中非常常見：比如

????????英漢詞典就是英文與中文的對應關系，通過英文可以快速找到與其對應的中文，英文單詞與其對應的中文<word, chinese>就構成一種鍵值對；

????????再比如統計單詞次數，統計成功后，給定單詞就可快速找到其出現的次數，單詞與其出現次數就是<word, count>就構成一種鍵值對

? ? ? ??KV模型二叉搜索樹

? ? ? ? KV模型實際上同K模型差不多，?只是在K模型的基礎上加了一個value值，對于其它的操作都是相似的，以下給出KV模型的整體代碼：

namespace kv
{template<class K, class V>struct BSTreeNode{BSTreeNode<K, V>* _left;BSTreeNode<K, V>* _right;K _key;V _value;BSTreeNode(const K& key, const V& value):_left(nullptr), _right(nullptr), _key(key), _value(value){}};template<class K, class V>class BSTree{typedef BSTreeNode<K, V> Node;public:bool Insert(const K& key, const V& value){if (_root == nullptr){_root = new Node(key, value);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){parent = cur;if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return false;}}cur = new Node(key, value);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return cur;}}return nullptr;}bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{// 準備刪除  20:15繼續if (cur->_left == nullptr){//左為空if (cur == _root){_root = cur->_right;}else{if (cur == parent->_left){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}}else if (cur->_right == nullptr){//右為空if (cur == _root){_root = cur->_left;}else{if (cur == parent->_left){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}}else{//左右都不為空// 右樹的最小節點(最左節點)Node* parent = cur;Node* subLeft = cur->_right;while (subLeft->_left){parent = subLeft;subLeft = subLeft->_left;}swap(cur->_key, subLeft->_key);if (subLeft == parent->_left)parent->_left = subLeft->_right;elseparent->_right = subLeft->_right;}return true;}}return false;}void InOrder(){_InOrder(_root);cout << endl;}private:void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << ":" << root->_value << endl;_InOrder(root->_right);}private:Node* _root = nullptr;};}

三、整體代碼?

#pragma once
#include<iostream>
using namespace std;namespace K
{//節點定義template<class K>struct BSTreeNode{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}};//二叉搜索樹template<class K>class BSTree{typedef BSTreeNode<K> Node;public://插入操作，按照左小右大的規則bool Insert(const K& key){if (_root == nullptr){_root = new Node(key);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){parent = cur;if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return false;}}cur = new Node(key);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}//查找操作bool Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return true;}}return false;}bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else//表示已經找到，進行刪除操作{//左為空的情況if (cur->_left == nullptr){if (cur == _root)//要刪即為根節點{_root = cur->_right;}else{if (cur == parent->_left)//因為左一定為空，為父節點的左子樹則將右半邊給父即可{parent->_left = cur->_right;}else//同理為父節點的右則將右半邊給父{parent->_right = cur->_right;}}delete cur;}else if (cur->_right == nullptr)//右為空的情況{//同理左為空if (cur == _root){_root = cur->_left;}else{if (cur == parent->_left){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}delete cur;}else//左右都不為空{//可以選擇找該節點左子樹的最大節點（最右節點）或者右子樹的最小節點（最左節點）//這里找右樹的最小節點(最左節點)Node* parent = cur;Node* subleft = cur->_right;while (subleft->_left){parent = subleft;subleft = subleft->_left;}swap(cur->_key, subleft->_key);//由于找到的是最左，則默認左為空,所以只需將右鏈接給父節點if (subleft == parent->_left){parent->_left = subleft->_right;}else{parent->_right = subleft->_right;}delete subleft;}return true;}}return false;}void InOrder()//中序遍歷即排升序{_InOrder(_root);cout << endl;}bool FindR(const K& key)//遞歸找{return _FindR(_root, key);}bool InsertR(const K& key)//遞歸插入{return _InsertR(_root, key);}bool EraseR(const K& key)//遞歸刪{return _EraseR(_root, key);}BSTree() = default;// C++11~BSTree(){Destroy(_root);}BSTree(const BSTree<K>& t){_root = Copy(t._root);}// t1 = t3BSTree<K>& operator=(BSTree<K> t){swap(_root, t._root);return *this;}private:Node* Copy(Node* root){if (root == nullptr)return nullptr;Node* newRoot = new Node(root->_key);newRoot->_left = Copy(root->_left);newRoot->_right = Copy(root->_right);return newRoot;}void Destroy(Node*& root){if (root == nullptr)return;Destroy(root->_left);Destroy(root->_right);delete root;root = nullptr;}bool _EraseR(Node*& root, const K& key){if (root == nullptr)return false;if (root->_key < key){return _EraseR(root->_right, key);}else if (root->_key > key){return _EraseR(root->_left, key);}else//找到了開始刪除{//實際上的操作同非遞歸差不多，這里巧妙的對root運用了引用if (root->_left == nullptr){Node* del = root;root = root->_right;delete del;return true;}else if (root->_right == nullptr){Node* del = root;root = root->_left;delete del;return true;}else//找右子樹的最大{Node* subleft = root->_right;while (subleft->_left){subleft = subleft->_left;}swap(root->_key, subleft->_key);// 轉換成在子樹去遞歸刪除return _EraseR(root->_right, key);}}}bool _InsertR(Node*& root, const K& key){if (root == nullptr){root = new Node(key);return true;}if (root->_key < key)return _InsertR(root->_right, key);else if (root->_key > key)return _InsertR(root->_left, key);elsereturn false;}bool _FindR(Node* root, const K& key){if (root == nullptr){return false;}if (root->_key < key){return _FindR(root->_right, key);}else if (root->_key > key){return _FindR(root->_left, key);}else{return true;}}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}Node* _root = nullptr;};
}namespace kv
{template<class K, class V>struct BSTreeNode{BSTreeNode<K, V>* _left;BSTreeNode<K, V>* _right;K _key;V _value;BSTreeNode(const K& key, const V& value):_left(nullptr), _right(nullptr), _key(key), _value(value){}};template<class K, class V>class BSTree{typedef BSTreeNode<K, V> Node;public:bool Insert(const K& key, const V& value){if (_root == nullptr){_root = new Node(key, value);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){parent = cur;if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return false;}}cur = new Node(key, value);if (parent->_key < key){parent->_right = cur;}else{parent->_left = cur;}return true;}Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_key < key){cur = cur->_right;}else if (cur->_key > key){cur = cur->_left;}else{return cur;}}return nullptr;}bool Erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key < key){parent = cur;cur = cur->_right;}else if (cur->_key > key){parent = cur;cur = cur->_left;}else{// 準備刪除  20:15繼續if (cur->_left == nullptr){//左為空if (cur == _root){_root = cur->_right;}else{if (cur == parent->_left){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}}else if (cur->_right == nullptr){//右為空if (cur == _root){_root = cur->_left;}else{if (cur == parent->_left){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}}else{//左右都不為空// 右樹的最小節點(最左節點)Node* parent = cur;Node* subLeft = cur->_right;while (subLeft->_left){parent = subLeft;subLeft = subLeft->_left;}swap(cur->_key, subLeft->_key);if (subLeft == parent->_left)parent->_left = subLeft->_right;elseparent->_right = subLeft->_right;}return true;}}return false;}void InOrder(){_InOrder(_root);cout << endl;}private:void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << ":" << root->_value << endl;_InOrder(root->_right);}private:Node* _root = nullptr;};}

????????????????????????感謝你耐心的看到這里?( ′･?･` )比心，如有哪里有錯誤請踢一腳作者o(╥﹏╥)o！?

????????????????????????????????? ? ? ?