進入貪心了,我覺得本專題是最燒腦的專題
Leetcode 455. 分發餅干
題目鏈接?455 分發餅干
讓大的餅干去滿足需求量大的孩子即是本題的思路:
class Solution {
public:int findContentChildren(vector<int>& g, vector<int>& s) {int sum = 0;sort(g.begin(),g.end());sort(s.begin(),s.end());int result = 0;int index = s.size()-1;for(int i=g.size()-1;i>=0;i--){//胃口if(index>=0&&s[index]>=g[i]){//餅干量result++;index--;}}return result;}
};ok,下面燒腦開始:
Leetcode 376. 擺動序列
題目鏈接?76 擺動序列
首先我們覺得本題目體現的貪心思想比較難想,我覺得這里應該用dp來寫,但是竟然有貪心思想,就是貪心題目,那就燒腦一下吧:
局部最優:刪除單調坡度上的節點(不包括單調坡度兩端的節點),那么這個坡度就可以有兩個局部峰值。
整體最優:整個序列有最多的局部峰值,從而達到最長擺動序列。
整體思路:

出現擺動就記錄一下。
對應代碼就是:
如果prediff < 0 && curdiff > 0?或者?prediff > 0 && curdiff < 0?此時就有波動就需要統計。
除此之外我們還要考慮三點:
第一點:上下坡中有平坡:
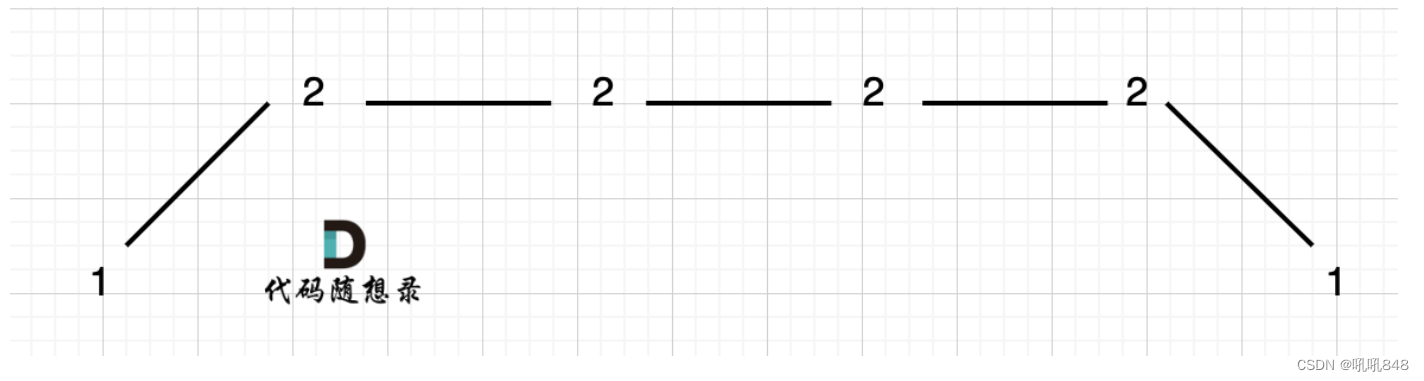
實際上我們取得擺動就三個,只需把中間四個2刪除三個就行,這里我們只需記錄即可,變成1——2——1即可,針對于代碼來說就是:

(preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0),我們有波動就需要統計。
第二點:數組首尾兩端
題目中說了,如果只有兩個不同的元素,那擺動序列也是 2。
這里我們就需要建立一個虛擬節點(虛擬節點和數組開頭組成preDiff == 0,即使平坡)使其滿足preDiff和curDiff兩邊需要三個節點最基礎的情況,這樣我們就可將第二種情況算到第一種情況的代碼中了:
(preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0),我們有波動就需要統計。
第三點:單調坡度有平坡(比較難想)

這時我們就不能實時更新preDiff了,我們只需在遇到(preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)即擺動時我們preDiff。
下面上代碼:
class Solution {
public:int wiggleMaxLength(vector<int>& nums) {int result = 0;int preDiff = 0;int curDiff = 0;result++;for(int i=0;i<nums.size()-1;i++){curDiff = nums[i+1]-nums[i];if(preDiff>=0&&curDiff<0||preDiff<=0&&curDiff>0){result++;preDiff = curDiff;//擺動時更新}}return result;}
};Leetcode 53. 最大子數組和
題目鏈接?53 最大子數組和
本題目很難發現需要使用貪心思想。
如果 -2 1 在一起,計算起點的時候,一定是從 1 開始計算,因為負數只會拉低總和,這就是貪心貪的地方!
局部最優:當前“連續和”為負數的時候立刻放棄,從下一個元素重新計算“連續和”,因為負數加上下一個元素 “連續和”只會越來越小。
全局最優:選取最大“連續和”
此外我們還需要不斷記錄連續和,找到最大的那個,就解決問題了。
下面上代碼:
class Solution {
public:int maxSubArray(vector<int>& nums) {int count = 0;int result = INT_MIN;for(int i=0;i<nums.size();i++){count+=nums[i];if(count>result){result = count;}if(count<=0){//連續和為負數,直接拋棄count = 0;}}return result;}
};end,學六級!!!
)

Vue生命周期、組件技術、事件總線、)


)








一招解決)



