題目描述

題目鏈接:力扣（LeetCode）官網 - 全球極客摯愛的技術成長平臺

題目分析

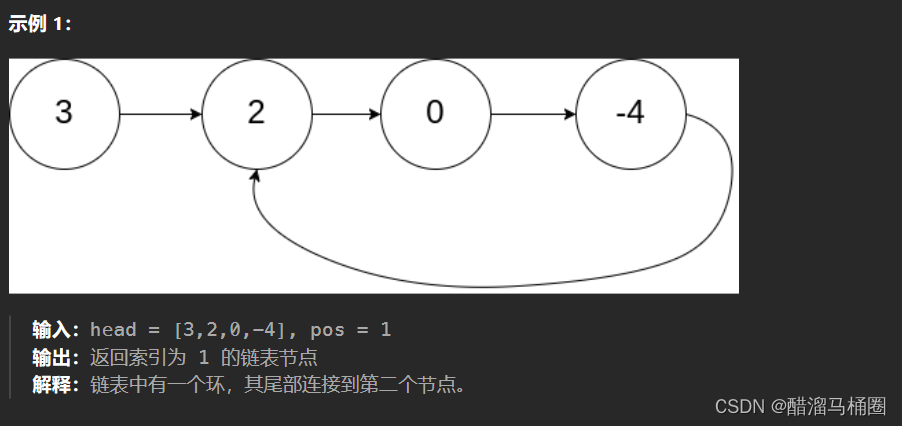
我們假設起點到環的入口點的距離是L，入口點到相遇點的距離是X，環的長度是C

那么畫圖我們可以得知：

• 從開始到相遇時slow走的距離是L+X
• 從開始到相遇時fast走的距離是L+n*C+X

（n:slow進環前，fast已經在環里走了?n 圈）

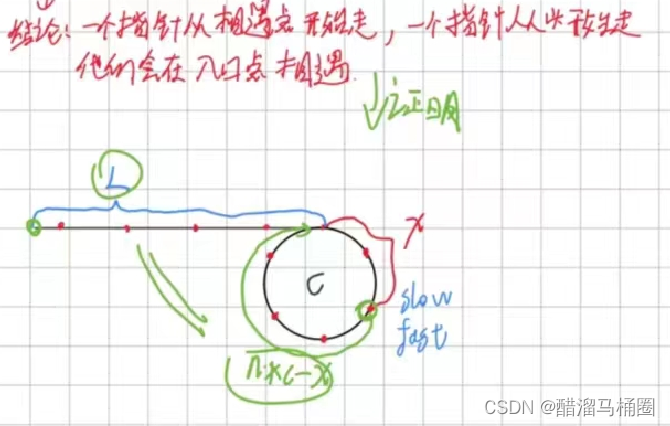
由于fast=slow*2，所以我們可以得到結論：一個指針從相遇點開始走，一個指針從頭開始走，最終會在入口點相遇

我們可以畫圖來證明一下：

代碼示例

根據這個思路我們可以寫出代碼:

/*** Definition for singly-linked list.* struct ListNode {*     int val;*     struct ListNode *next;* };*/
struct ListNode *detectCycle(struct ListNode *head) {struct ListNode *slow,* fast;slow=fast=head;while(fast&&fast->next){slow=slow->next;fast=fast->next->next;if(slow==fast)//相遇{struct ListNode *meet=slow;while(head!=meet){head=head->next;meet=meet->next;}return meet;}}return NULL;
}

結果當然也是通過了