大家好,不同的時間,相同的地點,時隔多日我們又見面了。繼上次的二分算法后,我們這次要來學習的是二分答案了。這個部分相較于前面的二分算法難度有相當的提升,希望大家有所準備。雖然難度增加了,但是博主還是會將其講明白講清楚的
let's go!
前言
二分算法雖然簡單但是它是很重要的,在某些題目當中,我們以后還會遇到,希望大家能夠有所重視。
1.二分答案
二分答案具體為:二分答案 + 判斷
當做算法題的時候,如果遇到最大值最小以及最小值最大的問題,就可以思考著去使用二分答案來解決了。二分答案可以幫助解決絕大多數這類的問題,如果解空間在從小到大的變化過程中,判斷答案的結果出現二段性,此時我們就可以去使用二分,去二分這個解空間,通過判斷來找出最優解。
可能大家看這個概念還是比較抽象,跟著博主做完下面三道題后大家就會明白了。
2.題目
P2440 木材加工 - 洛谷
P1873 [COCI 2011/2012 #5] EKO / 砍樹 - 洛谷
P2678 [NOIP 2015 提高組] 跳石頭 - 洛谷
大家可以先行做一下這幾道題,然后再看博主的思路。
3.木材加工
題目展示:
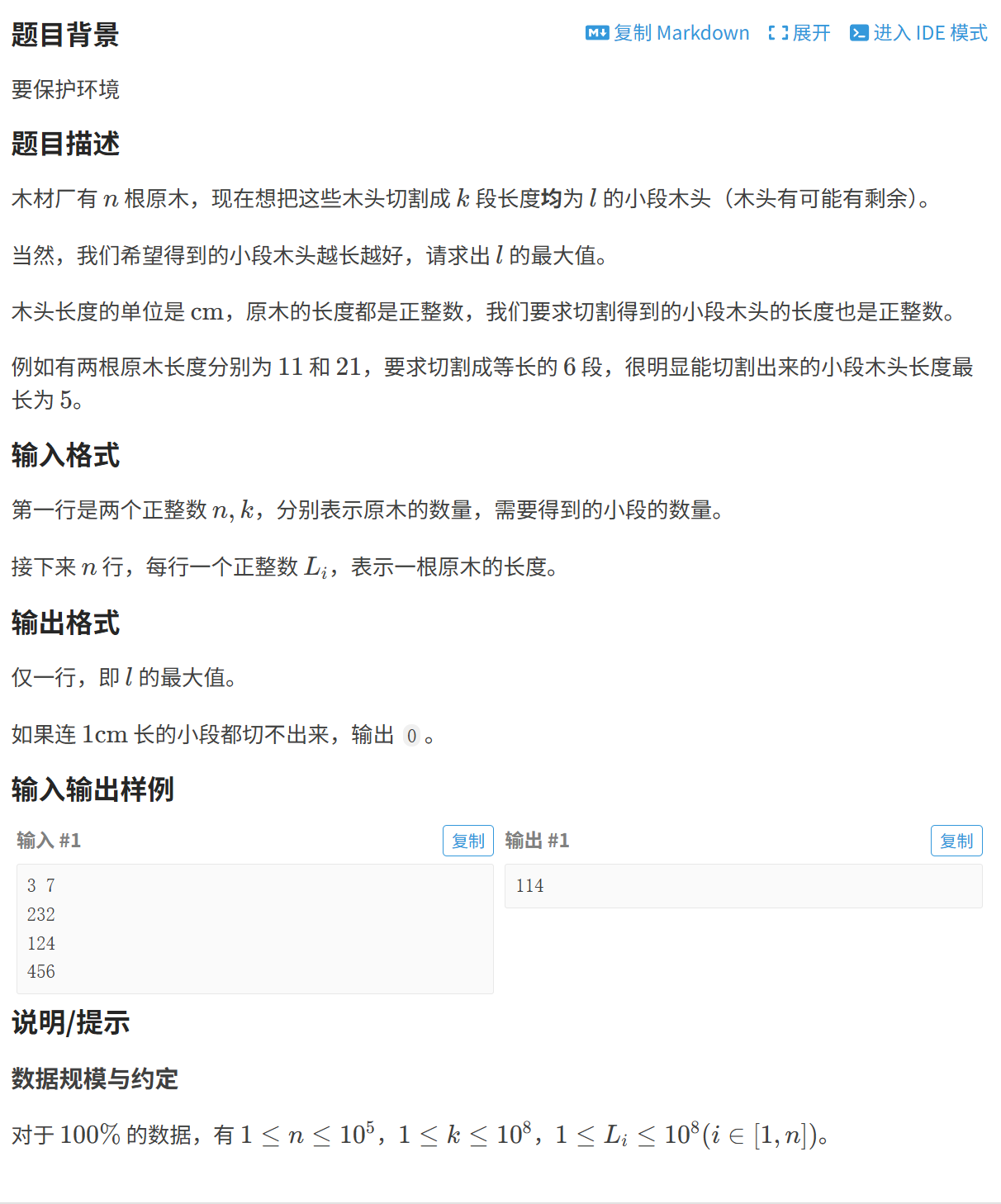
思路分析:
這道題可以說的上是二分答案的一道模版題目了,大家好好理解一下這道題:
大家看完題目后,應該有對題目有些理解了,那么我再來梳理一下這個題目吧。
這個題目會給出木頭n個和需要切割出來的木頭段數k,然后會給出n個木頭的長度a[i]
我們思考一下也就知道,如果我們將木頭切割成1cm的木頭(最短)那么我們肯定是可以滿足題目要求的段數,但是問題來了我們切割成1cm的小段不是能夠切割出來的最長?
那么我們一種暴力的解法就是:
暴力解法思路:
枚舉切割的長度從1到最長的木頭,然后開始通過這個切割長度x來計算段數(t) t = a[i] / x
通過將段數最后計算出來的和拿來和要求的k來比較,如果總和大于k就可以算是待正確答案。
這樣的話,我們可以將切割長度從最長的木頭長度往1開始減少的枚舉,這樣當第一次出現大于k的情況那個切割長度就是我們需要的答案
對于這個思路大家有興趣可以去實現一下,難度不大。
但是會出現超時的情況,我們就得用到二分答案的算法來解決這道題了。
二分答案思路:
如果我們所要的切割長度為ans,我們無非就是要在0~maxlen中找到這個答案ans
------------------------------------------
[0? ? ? ? ? ? ? ? ans? ? ? ? ? ? ? maxlen]
------------------------------------------
當枚舉的切割長度x在ans的左邊時,切割出來的段數 t >= k
當枚舉的切割長度x在ans的右邊時,切割出來的段數 t < k
所以這道題答案是具有二段性的,所以可以通過二分來解決
left ? ? ? ? ?mid ? ? ? ? ? ? right
calc(mid)計算當前切割長度能切多少段?
calc(mid) >= k ?left = mid;
calc(mid) < ?k ?right = mid - 1;
這時候后面的一個代碼實現就變得簡單很多了
代碼實現:
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
typedef long long LL;
LL n, k;
LL a[N];LL calc(LL x)
{//通過切割長度x計算切出的數量LL ret = 0;for (int i = 1; i <= n; i++){ret += a[i] / x; }return ret;
}int main()
{cin >> n >> k;LL r = 0;for (int i = 1; i <= n; i++){cin >> a[i];r = max(r, a[i]);}LL l = 0;while(l < r){LL mid = (l + r + 1) / 2;if (calc(mid) >= k) l = mid;else r = mid - 1;}cout << l << endl;return 0;
}
4.砍樹
題目展示:

思路分析:
這道題跟前面的那道題是很相似的大家看完前一道題后做這道題應該難度不會很大了。
但是現在還是跟著博主的思路開始分析一下這道題吧:
這道題給出了這一排樹的數目n,所需的木材m兩個數,接著給出了每棵樹的高度a[i]
我們需要找到一個合適的高度既能夠保護樹,也能滿足需求的木材。
那么我們的高度就只能是在0到最高的樹的高度來枚舉了
如果我們最后答案的樹高為ans
----------------------------------------------
[0? ? ? ? ? ? ? ? ? ?ans? ? ? ? ? ? ? ? ?maxh]
----------------------------------------------
當h小于ans時,獲得的木材 l >= m
當h大于ans時,獲得的木材 l < m
答案是具有二段性的,去思考使用二分答案來解決
left? ? ? ? ? ? ? ? ?mid? ? ? ? ? ? ? ? ?right
當枚舉樹高為mid,calc(mid)為此時獲得的木材
當calc(mid) >= m時,l = mid
當calc(mid) < m時,r = mid - 1
代碼實現:
#include <iostream>
using namespace std;
const int N = 1e6 + 10;
typedef long long LL;
LL n, m;
LL a[N];LL calc(LL x)
{// 計算出x樹高的時候,切割出來的木材數LL ret = 0;for (int i = 1; i <= n; i++){if (a[i] >= x) ret += a[i] - x;}return ret;
}
int main()
{cin >> n >> m;LL r = 0;for (int i = 1; i <= n; i++){cin >> a[i];r = max(r, a[i]);}LL l = 0;while(l < r){LL mid = (l + r + 1) / 2;if (calc(mid) >= m) l = mid;else r = mid - 1;}cout << l << endl;return 0;
}
5.跳石頭
題目展示:
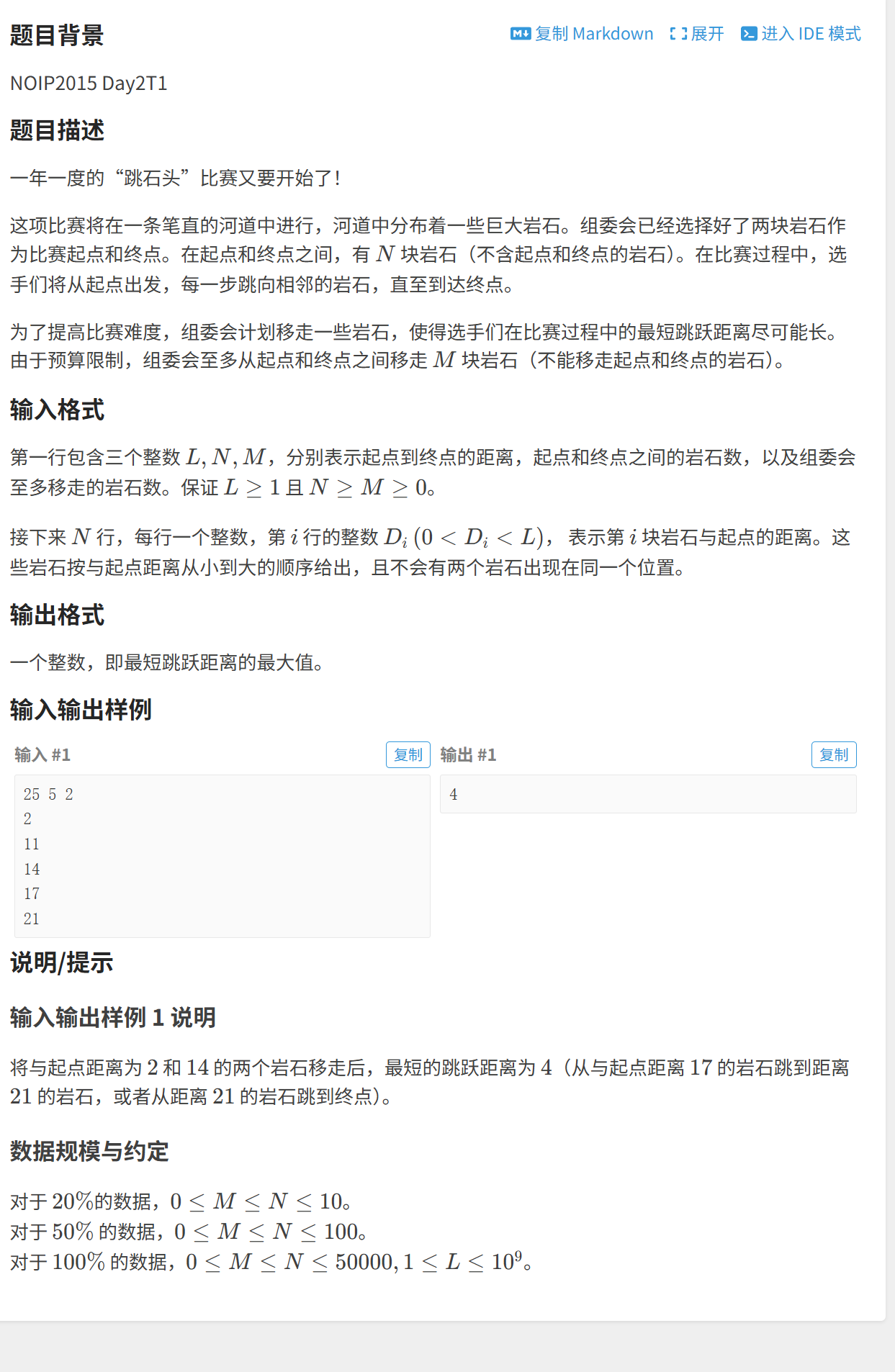
思路分析:
這道題題目可能剛看會有些不明白是怎么一回事,可以仔細看看
現在跟著博主的思路開始分析一下這道題目吧:
題目中會給出起點到終點的距離L,起點和終點之間的巖石數N,以及組委會至多移走的巖石數M
然后會給出N個值a[i],每個值a[i]代表第i個石頭距離起點的距離。
題目要我們求的是什么呢?讓我們求最短跳躍距離的最大值?
這是不是就是很符合我們二分答案嗎?
那么什么叫做最短跳躍距離的最大值呢?
由于移走石頭后選手會進行每塊石頭之間的跳躍,在所有跳躍中,會出現一個最短的跳躍距離
但是我們想要通過移走石頭來使得選手這個最短跳躍距離達到最大
最終要求出這個最短跳躍距離。
對于最短跳躍距離x,和移走石頭數c
當x增加,c也在增加
當x減小,c也在減少
-----------------------------------------------------------------
[1? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ans? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? L]
-----------------------------------------------------------------
當x <= ans時,移走的巖石小于等于 m
當x > ans時,移走的巖石c肯定大于 m (規定移走的巖石數)
left? ? ? ? ? ? ? ? ? ? ? ? mid? ? ? ? ? ? ? ? ? ? ? ?right
calc(mid)計算在最小跳躍距離為mid的時候,移走的石頭數
calc(mid) <= m ?在跳躍mid距離時,移走石頭小于等于m ?left = mid
calc(mid)?> ?m ?在跳躍mid距離時,移走石頭大于m ?right = mid - 1
那么問題來了?如何計算當最小跳躍距離為mid的時候,移走的石頭數呢?
這個地方我們可以通過雙指針的方法來實現它:
一個指針i指向前一個石頭,另外一個指針j向后查找,通過a[j] - a[i] < mid就讓j++
當出現a[j] - a[i] >= mid就停止向后查找,因為根據題目可以知道向后會越來越大
然后通過i和j的下標計算出來中間移走的石頭數量 j - i - 1
最后更新i的大小,i = j - 1 (因為在for循環里面還有一個i++) 讓i更新指向j的位置
然后繼續執行邏輯,最后得出這種情況的移走石頭數量。
這樣我們就可以去實現我們的代碼了!
代碼實現:
#include <iostream>
using namespace std;
const int N = 5e4 + 10;
typedef long long LL;
LL l, n, m;
LL a[N];
LL calc(LL x)
{//計算最短跳躍距離為x的時候,要移動的石頭數LL ret = 0;// 記錄石頭數// 遍歷石頭 for (int i = 0; i < n; i++){int j = i + 1;while(j <= n && a[j] - a[i] < x) j++;ret += j - i - 1;i = j - 1;}return ret;
}
int main()
{cin >> l >> n >> m;for (int i = 1; i <= n; i++){cin >> a[i]; // 巖石距離起點距離 }a[n + 1] = l;//避免計算的錯誤n++; LL left = 1, right = l;while(left < right){LL mid = (left + right + 1) / 2;if (calc(mid) <= m) left = mid;else right = mid - 1;}cout << left << endl;return 0;
}
結語
很高興大家能夠看到這里,希望前面內容的講解能夠給大家帶來收獲,弄懂二分答案的原理和使用場景,對于最后這道題可能比較難以理解,但是大家可以仔細思考思考。
如果這篇文章對您有所收獲的話,請多多點贊 + 收藏 + 關注!















變換)
)



)