【追求卓越11】算法--二叉樹

引導

????????接下來的幾節我們開始介紹非線性的數據結構--樹。樹的內容比較多也比較復雜。本節，我們只需要了解關于樹的一些基本概念。以及再進一步了解樹的相關內容--搜索二叉樹。該類型二叉樹在工作中，是我們常接觸的。該節我們介紹關于搜索二叉樹的相關操作：查找，插入，刪除。

什么是樹？

關于樹的定義：（摘自百度百科）

每個元素稱為結點（node）
有一個特定的結點被稱為根結點或樹根（root）
除根結點之外的其余數據元素被分為m（m≥0）個互不相交的集合T1，T2，……Tm-1，其中每一個集合Ti（1<=i<=m）本身也是一棵樹，被稱作原樹的子樹（subtree）

說實話，這段定義我看了好幾遍才能理解，對于剛接觸的同學，結合圖來理解是最好的了。

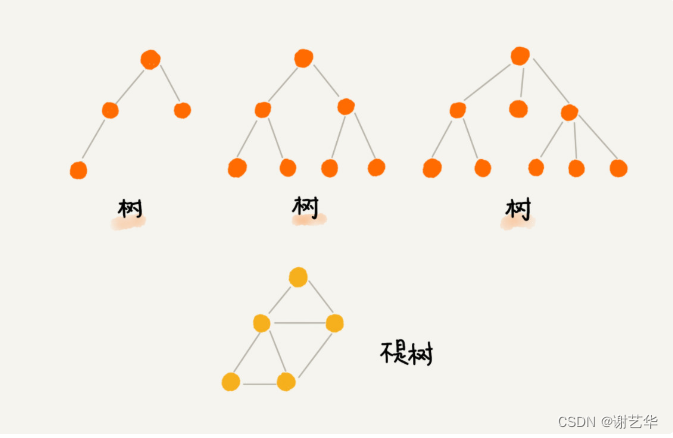
樹中有很多需要我們了解的名詞，我們結合下面的樹來介紹：

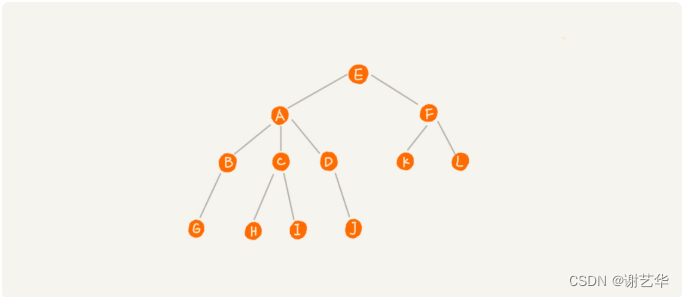
????????在上圖中,A節點就是B節點的父節點，B節點是A節點的子節點。B，C,D這三個節點有共同的父節點，他們是兄弟節點。我們把沒有父節點的節點稱作為根節點，也就是圖中的E節點。我們把沒有子節點的的節點稱作葉子節點或葉節點。

此外還有三個相似的概念：高度，深度，層。

節點的高度：節點到葉子節點最長路徑。比如，上圖中A節點的高度就是2.

節點的深度：根節點到節點的所經歷的邊數。比如，上圖中B節點的深度是2.

節點的層：節點的深度+1。比如，上圖中B子節點的層是3.

樹的高度：根節點的高度。比如，上圖中的樹的高度是3.

以上就是關于樹的部分名詞定義了。但是我們工作中常接觸的是二叉樹。接下來，我們來正式進入今天的主題。

二叉樹

????????二叉樹顧名思義，每個節點最多有兩個分支，即僅有兩個子節點。同理，有四個，八個分支的樹就是四叉樹，八叉樹。是不是很容易理解？如圖：

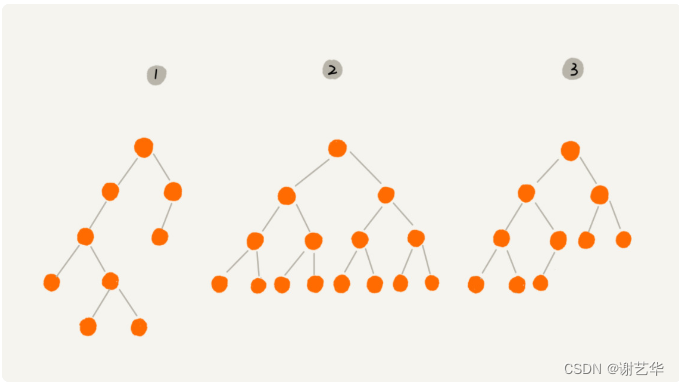
????????上圖中三個樹都是二叉樹，但是有兩個樹有比較特殊，需要注意。

????????其中2號樹中，葉子節點都在最低層，并且除了葉子節點，每個節點都有左右兩個字節點。這種二叉樹稱作為滿二叉樹。

????????其中3號樹中，葉子節點在最底下兩層，最后一層的葉子節點都是靠左排列，并且除了最后一層，其他層的節點個數達到最大數，這種樹稱作完全二叉樹。這個解釋我覺得還不是很清晰，摘自百度百科：對于深度為K的，有n個結點的二叉樹，當且僅當其每一個結點都與深度為K的滿二叉樹中編號從1至n的結點一一對應時稱之為完全二叉樹

????????到了這里，你可能會有疑問：滿二叉樹很容易理解，是二叉樹的一種特例。但是完全二叉樹存在的意義是什么？

二叉樹的存儲方式

????????我們常見的存儲方式是基于指針或者引用的二叉鏈式存儲法。他比較簡單和直觀，每個節點有一個數據段和兩個左右指針。如圖：

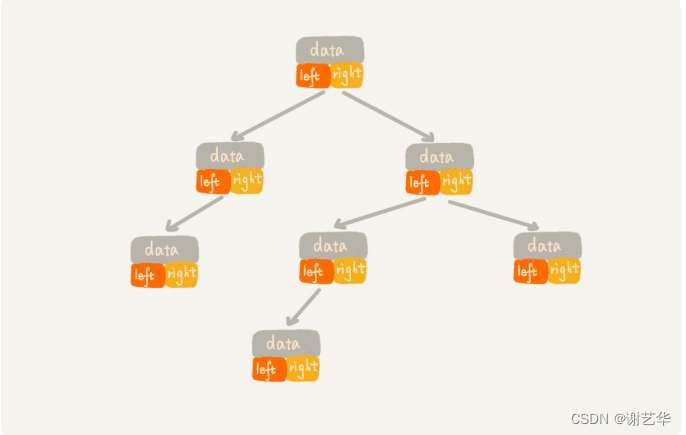
????????另一種就是基于數組的順序存儲法。我們把根節點存儲在下標i=1的位置，那左子節點存儲的下標2 * i=2的位置，右子節點存儲的下標2 * i+1的位置。

????????根據這樣的存儲方式，剛剛的完全二叉樹僅僅會浪費下標未0的空間，若不是完全二叉樹就會出現浪費內存空間的現象。如圖：

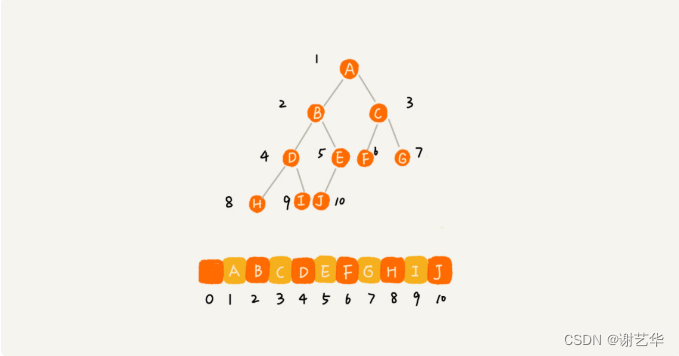
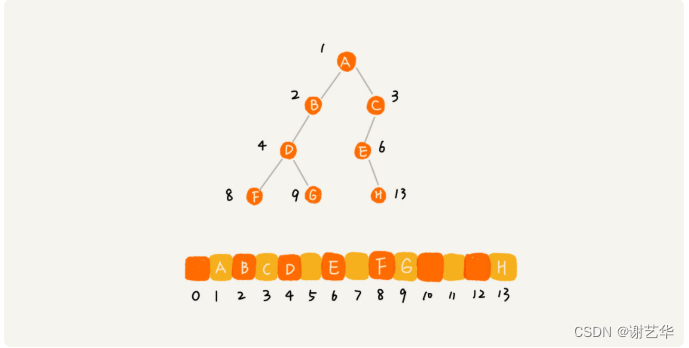
????????所以對于完全二叉樹，使用數組進行存儲是最省內存的一種方式。因為順序存儲方式比鏈式存儲方式更生內存，它不需要每個節點保存兩個指針變量。

二叉樹的遍歷

對于二叉樹的遍歷，這個也是非常常見的面試題。常見的遍歷方式是前序遍歷，中序遍歷，后序遍歷。

前序遍歷：對樹中任意節點，先打印這個節點，然后打印它的左子樹，最后打印右子樹。

中序遍歷：對于樹中任意節點，先打印這個節點的左子樹，然后打印該節點，最后打印右子樹。

后序遍歷：對于樹中任意節點，先打印這個節點的左子樹，然后打印右子樹，最后打印改節點。

對于遍歷，實現方式也很簡單，這里僅僅給出偽代碼

void preOrder(Node* root) {
? if (root == null) return;
? print root // 此處為偽代碼，表示打印root節點
? preOrder(root->left);
? preOrder(root->right);
}
void inOrder(Node* root) {
? if (root == null) return;
? inOrder(root->left);
? print root // 此處為偽代碼，表示打印root節點
? inOrder(root->right);
}
void postOrder(Node* root) {
? if (root == null) return;
? postOrder(root->left);
? postOrder(root->right);
? print root // 此處為偽代碼，表示打印root節點
}

每個節點最多被訪問兩次，故時間復雜度是O(n)。

搜索二叉樹

????????搜索二叉樹又稱為二叉查找樹。顧名思義，二叉查找樹是為了快速查找而誕生的。它不僅僅支持快速查找，還支持插入，刪除。

定義：二叉查找樹要求，在樹中任意一個節點，其左子樹中的每個節點的值，都要小于這個節點的值。而右子樹節點的值都大于這個節點的值。

可參考下圖：

搜索二叉樹的查找

先一個節點（一般是root節點），判斷是否是我們要查找的數據？
如果要查找的數據比該節點的大，我們就在右子樹中繼續查找
如果要查找的數據比該節點的小，我們就在左子樹中繼續查找
若未查找到，則返回空

從上面的思路可以看出，我們可以用遞歸或者循環來實現，下面貼上代碼(由于環境原因，代碼都沒有運行，不過代碼邏輯應該是這樣的)：

typedef strcut node{
??? int data;
??? struct node left;
??? struct node right;
}Node;
/
*while 循環*
/
Node * BinarySearchTree(Node* root , int target)
{
??? Node * p = root;
??? while(p != NULL)
??? {
??????? if(p.data == target)
??????????? return p;
??????? else if (p.data > target)
??????????? p = p.left;
??????? else
??????????? p = p.right;
??? }
??? return NULL;
}
/
*遞歸*
/
Node * BinarySearchTree(Node* root , int target)
{
??? if(root == NULL)
??????? return NULL;

??? if(root.data == target)
??? {
??????? return root;
??? }
??? else if(root.data > target)
??? {
??????? return BinarySearchTree(root.left,target);
??? }
??? else if(root.data < target)
??? {
??????? return BinarysearchTree(root.right,target);
??? }
}

搜索二叉樹的插入

????????插入操作和查找操作類似，新插入的數據一般都是保存在葉子節點上的。這句話，我剛開始是抱有懷疑態度，通過自己的思考也就理解了。建議大家先理解這句話的意思。

若知道了新插入數據都是保存在葉子節點上的，那么插入操作的思路也就簡單了。

思路：

先獲取一個節點，和插入數據比較哪個要大？
若要插入的數據比節點的值大，并且右子樹為空，即直接將數據插入到該節點的右子節點中。若不為空，繼續遍歷右子樹
若要插入的數據比節點的值小，并且左子樹為空，即直接將數據插入到該節點的左子節點中。若部位空，繼續遍歷左子樹

typedef strcut node{
??? int data;
??? struct node left;
??? struct node right;
}Node;
int BinarySearchInsert(Node * root , int target)
{
??? Node * p = root ;
??? while(p != NULL)
??? {
??????? if(p.data < target)
??????? {
??????????? if(p.right == NULL)
??????????? {
??????????????? p.right = newNode(target);
??????????????? return 0;
??????????? }
??????????? p = p.right;
??????? }
??????? else
??????? {
??????????? if(p.left == NULL)
??????????? {
??????????????? p.left = newNode(target);
??????????????? return 0;
??????????? }
??????????? p = p.left;
??????? }
??? }
??? return -1;
}

搜索二叉樹的刪除操作

搜索二叉樹的刪除操作就比較復雜了，因為刪除之后，你必須要保證剩下的樹結構滿足搜索二叉樹定義。其情況大致可以分為以下三種：

刪除節點沒有子節點。刪除一個節點，我們需要先找到這個節點，我們可以使用查找操作的邏輯。若刪除節點沒有子節點，也就不會影響樹的結構。直接刪除即可。將其父節點指向該節點的指針，指向NULL；
刪除的節點有一個子節點。將刪除節點的父節點指向該節點的指針修改為指向子節點即可。
刪除節點有兩個子節點。將刪除節點的右子樹中最小節點刪除，并替換為該刪除節點即可。這個可能比較抽象，可參數下圖,刪除18這個節點：

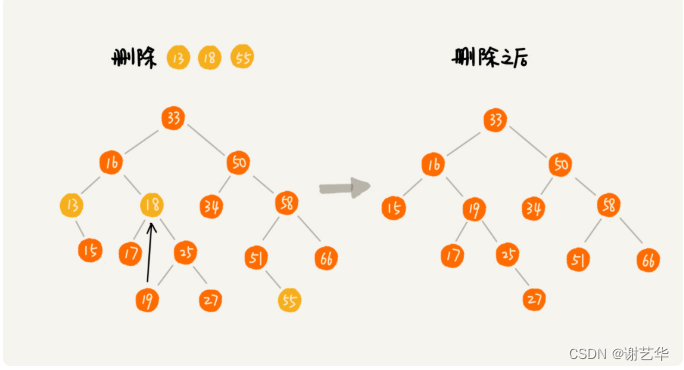
typedef strcut node{
??? int data;
??? struct node left;
??? struct node right;
}Node;
int BinarySearchDelete(Node * root , int target)
{
??? Node * p = root;
??? Node * father = NULL；
??? Node * minfather = NULL;
??? Node * min = NULL;
??? while(p != NULL && p.data != target)
??? {
??????? father = p; /
*保存父節點*
/
??????? if(p.data < target)
??????????? p = p.left;
??????? else
??????????? p = p.right;
??? }
??? if(p == NULL)
??????? return -1;/
*not find target*
/

??? /
*刪除節點有兩個子節點*
/
??? if(p.left != NULL && p.right != NULL)
??? {
??????? minfather = p;
??????? min = p.right;

??????? while(min.left != NULL )
??????????? minfather = min;
??????????? min = min.left;

??????? /
*至此找到刪除節點右子樹中的最小節點*
/
??????? p.data = min.data; /
*這里我覺得使用memcpy(p,min,sizeof(Node))較好*
/

??????? /
*將刪除的點變為只有一個或沒有子節點*
/
??????? p = min;
??????? father = minfather;
??? }

??? /
*至此，p表示刪除的節點，father表示刪除節點的父節點，并且刪除節點不會有兩個子節點*
/
??? Node * child = NULL;
??? if(p.left != NULL)
??????? child = p.left;
??? else if(p.right != NULL)
??????? child = p.right;

??? if(father == NULL)/
*刪除的是root節點*
/
??????? memcpy(root,child,sizeof(Node));
??? else if(father.left == p)
??????? father.left = child;
??? else
??????? father.right = child;

??? free(p);
}

搜索二叉樹的中序遍歷

????????搜索二叉樹有一個非常強大的特性，那就是通過中序遍歷，即可輸出有序的數據序列，時間復雜度是O(n),非常高效。

如何支持重復數據

上面的操作，我們都是假設沒有重復數據，但是顯示工作中我們總會遇到相同key的節點(key表示作為搜索二叉樹依據)。針對相同鍵值的節點，我們又有哪些方式處理呢？

利用數組或鏈表進行擴容，將相同鍵值的數據儲存到同一個節點上。
每個節點只保存一個數據。在插入的過程中，如果遇到一個節點的值，與要插入的值相同。我們就將這個要插入的數據放到這個節點的右子樹。也就是將這個新插入的數據當作大于這個節點的值來處理。后續的刪除都是按照這個邏輯處理

二叉查找樹的時間復雜度

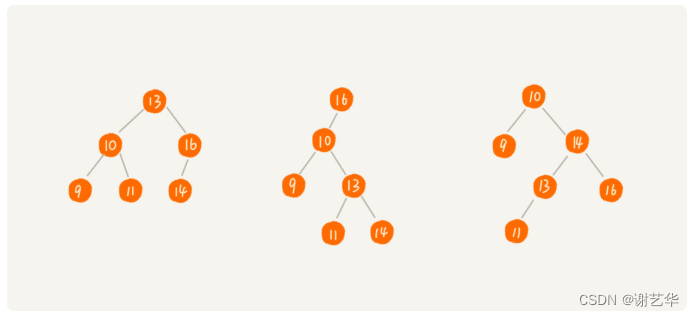
實際上二叉樹的形態各式各樣，即使同一組數據，也可以有不同的形態。如圖：

第一種情況完全退化成了鏈表，時間復雜度為O(n)，第三種的效果應該會好一些。其實，我們可以知道時間復雜度其實跟樹的高度成正比。也就是O(height)。根據完全二叉樹可知，L 的范圍是[log2(n+1), log2n +1]。這樣就極大的提高了效率。因此我們能在實際工作中需要無論怎么刪除或增加，都可以保證樹的平衡。紅黑樹就是這樣的一種樹。時間復雜度為O(logn)