🤵?♂? 個人主頁: @AI_magician
📡主頁地址： 作者簡介：CSDN內容合伙人，全棧領域優質創作者。
👨?💻景愿：旨在于能和更多的熱愛計算機的伙伴一起成長！！🐱?🏍
🙋?♂?聲明：本人目前大學就讀于大二，研究興趣方向人工智能&硬件（雖然硬件還沒開始玩，但一直很感興趣！希望大佬帶帶）

【深度學習 | 核心概念】那些深度學習路上必經的核心概念，確定不來看看？ （一） 作者： 計算機魔術師 版本： 1.0 （ 2023.8.27 ）

---

摘要： 本系列旨在普及那些深度學習路上必經的核心概念，文章內容都是博主用心學習收集所寫，歡迎大家三聯支持！本系列會一直更新，核心概念系列會一直更新！歡迎大家訂閱

該文章收錄專欄
[?— 《深入解析機器學習：從原理到應用的全面指南》 —?]

白噪聲檢驗

白噪聲序列是一種在統計學和信號處理中常見的隨機過程。它具有一些特定的特性，使其在各個頻率上具有均勻的能量分布。由一系列相互獨立、具有相同概率分布的隨機變量組成的。這些隨機變量之間沒有任何相關性，因此在時間上是完全不相關的。這意味著序列中的每個值都是獨立地從相同的概率分布中生成的。

其名稱來源于光學中的類比。在光學中，白光是由各種頻率的光波混合而成的，這些光波具有均勻的能量分布。類似地，白噪聲序列在頻率域上具有均勻的能量分布，從低頻到高頻都有相似的能量。

白噪聲序列在許多領域中都有應用，包括信號處理、通信系統、金融市場建模等。它常被用作基準參考，用于比較其他信號或系統的性能。此外，白噪聲序列還用于測試和校準設備，以及進行隨機性分析和模擬實驗。

在時間序列中，白噪聲檢驗除了用于在預測前判斷平穩序列是否隨機外，還能有哪些用法呢？

-- 檢驗殘差是否為白噪聲，判斷模型擬合的是否足夠好，是否還存在有價值的信息待提取。

\1. 殘差為白噪聲，說明模型擬合的很好，殘差部分為無法捕捉的純隨機數據。
\2. 殘差非白噪聲，說明模型哪里出了問題，比如參數沒調好，需要繼續優化；若如何優化模型也無法使得殘差為白噪聲，換模型或者集成模型，或者對殘差進行二次預測。

白噪聲的定義很簡單，只要滿足以下3個條件即可：
\1) E(εt)=μ
\2) Var(εt)=σ2
\3) Cov(εt,εs)=0,t≠s
另外一種常見的定義方式為一個具有零均值同方差的獨立同分布的序列為白噪聲。

白噪聲檢驗方法常用有以下3種方法（自相關圖、Box-Pierce檢驗、Ljung-Box檢驗），其中Ljung-Box檢驗相對用的多一些，在調用statsmodels庫的acf函數計算自相關系數時，指定qstat=True，會同時返回對應滯后期數下的Ljung-Box檢驗結果。

自相關圖

由定義知，白噪聲完全無自相關性，除0階自相關系數為1外，理想情況下?k,(k>0) ，延遲k階的樣本自相關系數均為0。實際上由于樣本序列的有限性，延遲k階自相關系數并不完全為0，只要在0值附近即認為無自相關性。

由于隨機擾動的存在，自相關系數并不嚴格等于0，我們期望在95%的置信度下，即相關系數均在 ±2/T 之間。如果一個序列中有較多自相關系數的值在邊界之外，那么該序列很可能不是白噪聲序列。上圖中自相關系數均在邊界之內，為白噪聲序列。

Ljung-Box檢驗

實際應用中人們發現 Q 統計量在大樣本場合( n 很大的場合)檢驗效果很好（傳統檢驗方法中樣本量大于30即認為大樣本量，Joel等人指出當樣本量在500這個量級時 Q 統計量檢驗效果較好），但是在小樣本場合不太精確。為了彌補這一缺陷，Box和Ljung于1979年對其進行了改進，推導出LB(Ljung-Box)統計量。

假設條件：

• H0:ρ1=ρ2=…=ρm=0 （滯后m階序列值之間相互獨立，序列為獨立同分布的白噪聲）
• H1:?ρk≠0$,1<=k<=m （滯后 m 階序列值之間有相關性，序列為非獨立同分布的白噪聲）
  其中， ρk 為延遲k階的自相關系數， m 為最大延遲階數。

檢驗統計量： $Q_{LB}=n(n+2){\sum }_{k=1}^m{\rho }_k^2/n?k$

LB統計量同樣近似服從自由度為 m 的 χ2 分布。其中， n 為序列觀察期數， m 為指定的最大延遲階數， ρ^__k 為延遲 k 階自相關系數的估計值。

由于LB統計量就是Box和Pierce的Q統計量的修正，所以人們習慣把它們統稱為Q統計量。

判斷準則：

LB統計量小于選定置信水平下的臨界值，或者 p 值大于顯著性水平（如0.05），不能拒絕原假設，序列為白噪聲；

LB統計量大于選定置信水平下的臨界值，或者 p 值小于顯著性水平（如0.05），拒絕原假設，序列非白噪聲；

實踐環節：

序列檢驗

import numpy as np
import matplotlib.pyplot as plt
from statsmodels.stats.diagnostic import acorr_ljungboxnp.random.seed(123)
# 白噪音
white_noise=np.random.standard_normal(size=100)# 不再指定boxpierce參數，近返回QLB統計量檢驗結果
# 同時設置lags參數為一個列表，相應只返回對應延遲階數的檢驗結果
res = acorr_ljungbox(white_noise, lags=[6,12,24,48], return_df=True)
print(res)

延遲6階、12階時 p值較大，增加到延遲24階時，p值略小但也大于0.05，所以在95%的置信水平下認為序列為白噪聲。（這部分則是隨機序列的偶然因素了）

還有一種實現Ljung-Box檢驗的方式為，調用statsmodels包中的acf函數，計算自相關系數時指定qstat為True，表示返回結果中除返回自相關系數外，另返回自相關系數的獨立性檢驗結果 QLB 統計量及對應 p 值。

import numpy as np
import pandas as pd
import statsmodels as smnp.random.seed(123)
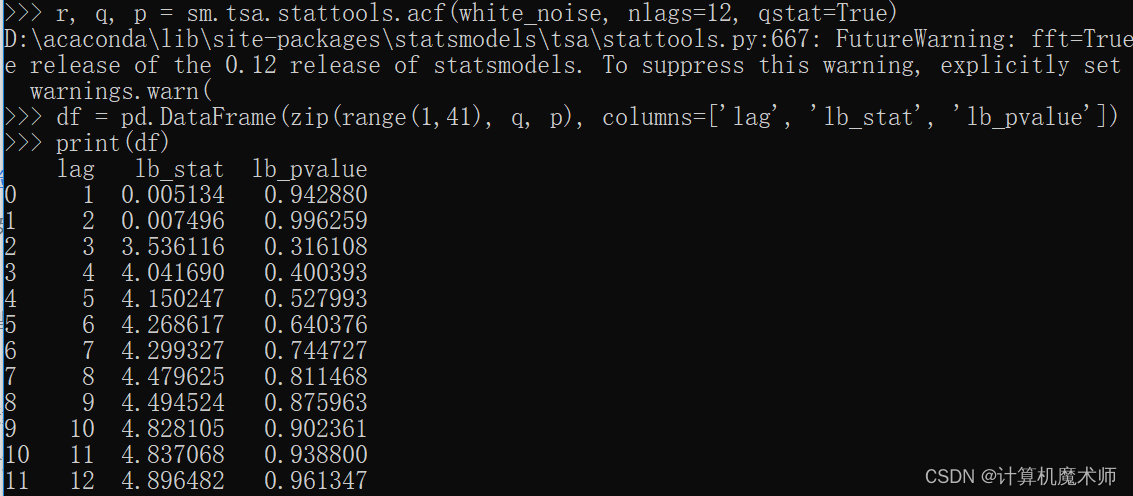
white_noise=np.random.standard_normal(size=100)r, q, p = sm.tsa.stattools.acf(white_noise, nlags=12, qstat=True) # 額外返回q p 統計量
df = pd.DataFrame(zip(range(1,41), q, p), columns=['lag', 'lb_stat', 'lb_pvalue'])
print(df)

舉一個為非白噪聲的例子（太陽黑子）

import matplotlib.pyplot as plt
import statsmodels.api as sm
data = sm.datasets.sunspots.load_pandas().data
data = data.set_index('YEAR')res = acorr_ljungbox(data.SUNACTIVITY, lags=[6,12,24], boxpierce=True, return_df=True)
print(res)data.plot(figsize=(12, 4))
plt.show()

在這里插入圖片描述

顯而易見的數據有著周期性。

模型效果檢驗

而在檢驗模型效果的應用中，假設我們有一個時間序列數據如下：

[1.2, 2.4, 3.1, 4.6, 5.3, 6.8, 7.5, 8.9, 9.7, 10.2]

我們可以使用ARIMA模型對該數據進行擬合，并得到殘差序列。然后，我們可以進行Ljung-Box白噪聲檢驗來判斷殘差序列是否存在自相關。

import numpy as np
from statsmodels.tsa.arima_model import ARIMA
from statsmodels.stats.diagnostic import acorr_ljungbox# 原始數據
data = np.array([1.2, 2.4, 3.1, 4.6, 5.3, 6.8, 7.5, 8.9, 9.7, 10.2])# 擬合ARIMA模型，得到殘差序列
model = ARIMA(data, order=(1, 0, 0))  # 這里以ARIMA(1, 0, 0)為例
model_fit = model.fit(disp=0)
residuals = model_fit.resid # 訓練數據中的殘差# 進行Ljung-Box白噪聲檢驗
lbvalue, pvalue = acorr_ljungbox(residuals, lags=5)  # 檢驗前5個滯后期# 打印檢驗結果
print("Ljung-Box白噪聲檢驗結果：")
for lag, p in enumerate(pvalue):print(f"滯后期{lag+1}：p-value={p}")

運行以上代碼，我們可以得到如下的檢驗結果：

Ljung-Box白噪聲檢驗結果：
滯后期1：p-value=0.8811740567913574
滯后期2：p-value=0.9395957812016121
滯后期3：p-value=0.9444992061584102
滯后期4：p-value=0.9826682340484362
滯后期5：p-value=0.9658631275329448

在這個案例中，我們可以看到每個滯后期的p-value都遠大于0.05，意味著殘差序列在這些滯后期上沒有顯著的自相關。因此，我們可以認為殘差序列是一個白噪聲序列，即沒有自相關（模型效果優秀）。

參考文章：

https://zhuanlan.zhihu.com/p/430365631

						  🤞到這里，如果還有什么疑問🤞🎩歡迎私信博主問題哦，博主會盡自己能力為你解答疑惑的！🎩🥳如果對你有幫助，你的贊是對博主最大的支持！！🥳