有文本串aabaabaaf,模式串aabaaf問文本串中是否出現過模式串
暴力解法
最不用動腦子的,直接兩層for循環,逐個匹配,匹配到不相等的值時把文本串后移一位,再重新比較。這種方法的復雜度是O(m×n),該方法低效的原因在于重復比較次數過多,比如當比較到aabaa時發現此時的f與b不相符,又從頭開始比較,但ff和b前有相同的aa,如果我們能直接從b開始比較是不是高效多了呢?由此產生了KMP算法。
KMP算法概述
KMP算法就是當模式串與文本串字符不等時,不移動至頭部進行比較,比如f與b不匹配,跳至b進行比較,節約了前面相同aa的比較次數,嘗試將比較過程直觀展示如下:
逐個比較到f發現不匹配
a a b a a b a a f
| | | | | !=
a a b a a f
此時再從之前已知匹配的aa后面的b開始比較即可
a a b a a b a a f| | | | | |a a b a a f
那我們如何得知之前匹配的內容呢?這時就要引入前綴表的概念。
前綴表
a a b a a f
0 1 0 1 2 0
形如上表這樣,比較到當前字符發現不匹配時,可由前一位對應的字符找到此時應跳轉的位置,這樣的表為前綴表,具體如何找到對應字符應跳轉的位置,要先引入前后綴的概念。
前綴為包含首字母,不包含尾字母的所有字串;后綴為包含尾字母,不包含首字母的所有字串,以該模式串為例,其所有前綴和后綴為:
前綴:a aa aab aaba aabaa
后綴:f af aaf baaf abaaf
模式串不同字串對應的最長相等前后綴表格如下:
a aa aab aaba aabaa aabaaf
0 1 0 1 2 0
a a b a a f
當不匹配時找前一個字符最長相等前后綴即可,在編程中我們將其命名為next數組。
next數組代碼示例
a a b a a f
j i
0
void getNext(next,s)//s為模式串{ j=0;next[0]=0;//初始化,i,j表示后前綴末尾指向位置for(i=1;i<s.size();i++){//后綴指向1,第一個字符無后綴,故其最長相等前后綴為0while(j>0&&s[i]!=s[j])//當前后綴不等時,j等于前一個字符對應的next數組位置j=next[j-1];if(s[i]==s[j]//前后綴相等時,j后移一位,i的后移在循環中實現j++;next[i]=j;}保存next數組}
}
該代碼實現了next數組即解決了如果當下不滿足時該從何處比較的問題,也就是求出不同字符串下最長相等前后綴,方式是比較前后綴的最后一位來判定,那我想比較前后綴相同不是還要通過兩個for循環來實現嗎,為什么比較前后綴的最后一位就能判定兩個不同的字符串最大相等前后綴長度呢?
當前后綴相等時我們很好理解,因為前面的相等已經判斷過了,所以如果當下判定位置仍相等時,只需在上一次結果上+1即可;主要是當下判定位置不等時如何理解,執行步驟是向前遍歷,直至找到與后綴字符相等的字符,并將前綴末尾指向之,想了半天又看了幾遍實在不明白咋回事,貼兩張圖看看能不能理解吧,好像用到了動態規劃的思想?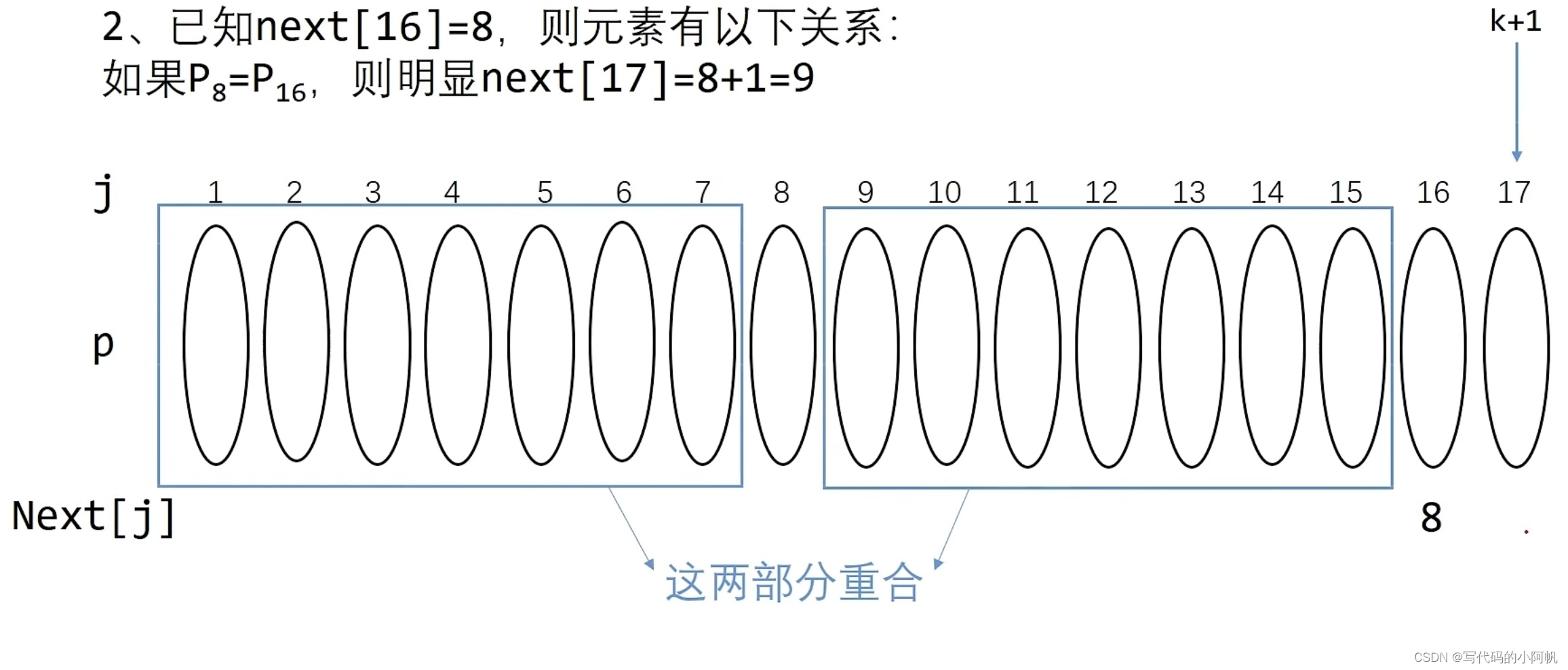

總結
KMP算法是用于比較字符串的一種高效算法,特點在于字符串只向前,模式串節約了重復部分的比較次數,實現通過next數組,但涉及next數組的求解人家有很巧妙的辦法,五行代碼就給搞定了,比我手算還簡單,沒有明白,暫時就到此為止吧。
)





)

)


)
)




)

