文章目錄
- 題目描述
- 思路分析
- 完整代碼
題目描述
給定三個字符串 s1、s2、s3,請你幫忙驗證 s3 是否是由 s1 和 s2 交錯 組成的。
兩個字符串 s 和 t 交錯 的定義與過程如下,其中每個字符串都會被分割成若干 非空 子字符串:
s = s1 + s2 + … + sn
t = t1 + t2 + … + tm
|n - m| <= 1
交錯 是 s1 + t1 + s2 + t2 + s3 + t3 + … 或者 t1 + s1 + t2 + s2 + t3 + s3 + …
注意:a + b 意味著字符串 a 和 b 連接。
示例 1:
輸入:s1 = “aabcc”, s2 = “dbbca”, s3 = “aadbbcbcac”
輸出:true
思路分析
動規題。
1.確定dp數組含義:
dp[i][j] 表示s1前i個字符和s2前j個字符能否構成s3的前i+j個字符。
2.分析遞推公式:
由于需要s1+s2來構成s3,所以設想子問題s3的最后一個字符是由誰構成的。
- 若s3的最后一個字符由s1提供,則有:s3[i+j] = s1[i],而 s3 此前的 i+j?1個字符,可由 s1 的前 i?1 字符和 s2 的前 j 個字符共同提供。這時候就要去判斷dp數組的上一個狀態了,即若 dp[i?1][j]為真,則 dp[i][j]為真。
- 若s3最后一個字符由s2提供,則同理
if s1[i-1] == s3[i+j-1] and dp[i-1][j]:dp[i][j] = Trueif s2[j-1] == s3[i+j-1] and dp[i][j-1]:dp[i][j] = True別忘了 dp[i][j] 表示s1前i個字符(不包含i)3.初始化
由于為了方便,所以數組都從下標1開始。
在初始化的時候 多開一行一列的dp數組。
必有:dp [0][0] = True。
dp的第二行和第二列也需要初始化,就直接比較當前s1或者s2字符和當前的s3字符是否相等,如果相等,看看前一個dp位置是否也是True,如果是則當前dp位置也是True。
for i in range(1, n + 1):dp [i][0] = dp [i - 1][0] and s1[i - 1] == s3[i - 1]
for i in range(1, m + 1):dp [0][i] = dp [0][i - 1] and s2[i - 1] == s3[i - 1]
完整代碼
class Solution:def isInterleave(self, s1: str, s2: str, s3: str) -> bool:# dp[i][j] 表示s1前i個字符和s2前j個字符能否構成s3的前i+j個字符n, m, l = len(s1), len(s2), len(s3)if n + m != l:return Falsedp = [[False] * (m + 1) for _ in range(n + 1)]dp [0][0] = Truefor i in range(1, n + 1):dp [i][0] = dp [i - 1][0] and s1[i - 1] == s3[i - 1]for i in range(1, m + 1):dp [0][i] = dp [0][i - 1] and s2[i - 1] == s3[i - 1]for i in range(1,n+1):for j in range(1,m+1):if s1[i-1] == s3[i+j-1] and dp[i-1][j]:dp[i][j] = Trueif s2[j-1] == s3[i+j-1] and dp[i][j-1]:dp[i][j] = Truereturn dp[-1][-1]```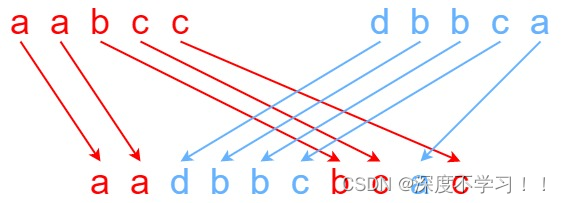

)
:Python Imaging Library(PIL)庫:圖像讀取、寫入、復制、粘貼、幾何變換、圖像增強、圖像濾波)










)




)
