D-VRNN模型和DD-VRNN模型

總體架構

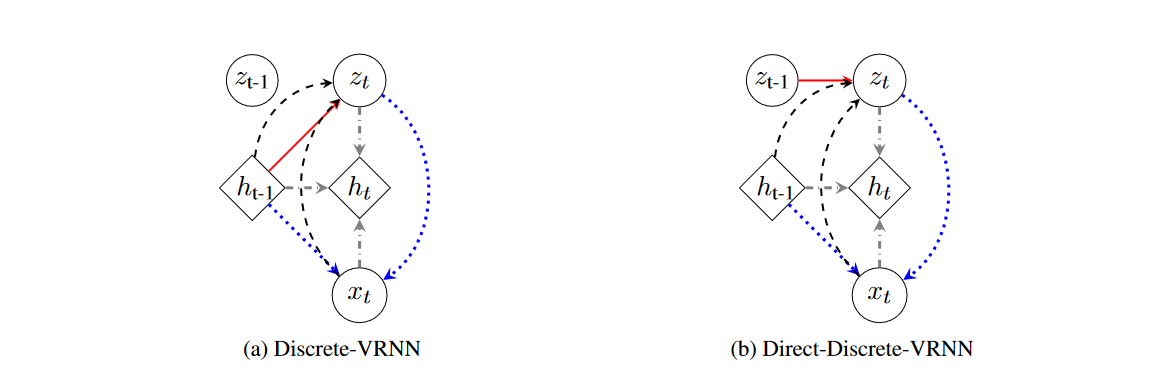
離散-可變循環變分自編碼器（D-VRNN）和直接-離散-可變循環變分自編碼器（DD-VRNN）概述。D-VRNN和DD-VRNN使用不同的先驗分布來建模$z_t$之間的轉換，如紅色實線所示。$x_t$的再生成用藍色虛線表示。狀態級別的循環神經網絡的循環關系以灰色虛線點劃線表示。$z_t$的推斷過程以黑色虛線表示。

方法

原則上，變分遞歸神經網絡（VRNN）在每個時間步都包含一個變分自編碼器（VAE），這些VAE通過一個狀態級的遞歸神經網絡（RNN）相連。在這個RNN中，隱藏狀態變量 $h_{t?1}$ 編碼了直到時間 $t$ 的對話上下文。這種連接幫助VRNN模擬對話的時間結構（Chung等人，2015年）。模型的觀測輸入 $x_t$ 是構建的話語嵌入。$z_t$ 是時間 $t$ 時VRNN中的潛在向量。與Chung等人（2015年）的工作不同，我們模型中的 $z_t$ 是一個離散的獨熱向量，其維度為 $N$，其中 $N$ 是潛在狀態的總數。

D-VRNN與DD-VRNN之間的主要區別在于 $z_t$ 的先驗設定。在D-VRNN中，我們假設 $z_t$ 依賴于整個對話上下文 $h_{t?1}$，如圖(a)中紅色部分所示，這與Chung等人（2015年）的設定相同；而在DD-VRNN中，我們假設在先驗中，$z_t$ 直接依賴于 $z_{t?1}$，以模擬不同潛在狀態之間的直接轉換，如圖(b)中紅色部分所示。我們使用 $z_t$ 和 $h_{t?1}$ 來重新生成當前話語 $x_t$，而不是生成下一個話語 $x_{t+1}$，如圖1中藍色虛線所示。重生成的思想有助于恢復對話結構。接下來，遞歸神經網絡利用 $h_{t?1}$，$x_t$ 和 $z_t$ 更新自身，并允許上下文隨著對話的進行而傳遞，如圖1中灰色點劃線所示。最后，在推斷中，我們用上下文 $h_{t?1}$ 和 $x_t$ 構建 $z_t$ 的后驗，并通過從后驗中抽樣來推斷 $z_t$，如圖1中黑色虛線所示。每個操作的數學細節在下文中描述。φ(·)τ 是高度靈活的特征提取函數，如神經網絡。${\phi }_{\tau }^x$ ，$\phi z\tau$ ，${\phi }_{\tau }^{prior}$ ，${\phi }_{\tau }^{enc}$ ，${\phi }_{\tau }^{dec}$ 是分別用于輸入 $x$，潛在向量 $z$，先驗，編碼器和解碼器的特征提取網絡。

句子嵌入

用戶話語 $u_t=[w_{1,t},w_{2,t},\dots ,w_{n_w,t}]$ 和系統話語 $s_t=[v_{1,t},v_{2,t},\dots ,v_{n_v,t}]$ 是在時間 $t$ 的用戶話語和系統話語，其中 $w_{i,j}$ 和 $v_{i,j}$ 是單獨的詞語。兩方話語的連接，$x_t=[u_t,s_t]$，是VAE中的觀測變量。我們使用Mikolov等人（2013年）的方法來進行詞嵌入，并對 $u_t$ 和 $s_t$ 的詞嵌入向量進行平均，得到 ${\tilde{u}}_t$ 和 ${\tilde{s}}_t$。${\tilde{u}}_t$ 和 ${\tilde{s}}_t$ 的連接被用作 $x_t$ 的特征提取，即 ${?}_{\tau }^x(x_t)=[{\tilde{u}}_t,{\tilde{s}}_t]$。${?}_{\tau }^x(x_t)$ 是模型的輸入。

Prior in D-VRNN

在D-VRNN中，先驗是我們在觀察數據之前對 $z_t$ 的假設。在D-VRNN中，假設 $z_t$ 的先驗依賴于上下文 $h_{t?1}$，并遵循公式（1）中顯示的分布是合理的，因為對話上下文是影響對話轉換的關鍵因素。由于 $z_t$ 是離散的，我們使用softmax函數來獲取分布。

$$z_t～\text{softmax}({?}_{\tau }^{\text{prior}}(h_{t?1}))\text{\hspace{1em}(1)}$$

Prior in DD-VRNN

DD-VRNN中的先驗。$z_t$ 在公式（1）中對整個上下文 $h_{t?1}$ 的依賴性，使得我們難以解開 $z_{t?1}$ 與 $z_t$ 之間的關系。但這種關系對于解碼對話交換如何從一次流向下一次至關重要。因此，在DD-VRNN中，我們直接在先驗中模擬 $z_{t?1}$ 對 $z_t$ 的影響，如公式（2）和圖1(b)所示。為了將這個先驗分布適配到變分推斷框架中，我們用公式（3）中的 $p(z_t|z_{t?1})$ 來近似 $p(x_t|z_t,z_t)$。稍后，我們將展示設計的新先驗在特定場景下的優勢。
$$z_t～\text{softmax}({?}_{\tau }^{\text{prior}}(z_{t?1})[]\text{\hspace{1em}(2)}$$

它表示潛在狀態 $z_t$ 的先驗分布直接依賴于前一時間步的潛在狀態 $z_{t?1}$，并通過特征提取函數 ${?}_{\tau }^{\text{prior}}$ 映射和softmax函數來確定。

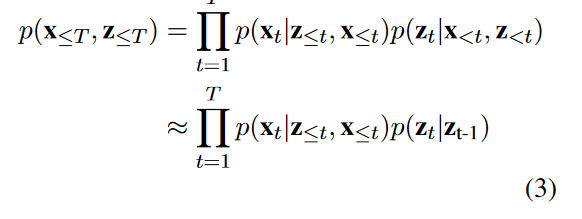
模型整體的概率分布可以近似為：
$$p(x_{\le T},z_{\le T})\approx \prod _{t=1}^{T}p(x_t|z_{\le t},x_{<t})p(z_t|z_{t?1})\text{\hspace{1em}(3)}$$

生成

$z_t$ 是在上下文下當前對話交換的概括。我們使用 $z_t$ 和 $h_{t?1}$ 來重構當前的話語 $x_t$。這種 $x_t$ 的重生產允許我們恢復對話結構。

我們使用兩個RNN解碼器，dec1和dec2，分別由參數 ${\gamma }_1$ 和 ${\gamma }_2$ 參數化，以分別生成原始的 $u_t$ 和 $s_t$。$c_t$ 和 $d_t$ 是dec1和dec2的隱藏狀態。上下文 $h_{t?1}$ 和特征提取向量 ${?}_{\tau }^z(z_t)$ 被連接起來，形成dec1的初始隱藏狀態 $h_0^{\text{dec1}}$。$c(n_w,t)$ 是dec1的最后一個隱藏狀態。由于 $v_t$ 是 $u_t$ 的響應，并且會受到 $u_t$ 的影響，我們將 $c(n_w,t)$ 與 $d_0$ 連接起來，將信息從 $u_t$ 傳遞給 $v_t$。這個連接向量被用作dec2的 $h_0^{\text{dec2}}$。這個過程在公式（4）和（5）中顯示。

$$c_0=[h_{t?1},{?}_{\tau }^z(z_t)]$$
$$w(i,t),c(i,t)=f_{{\gamma }_1}(w(i?1,t),c(i?1,t))\text{\hspace{1em}(4)}$$

$$d_0=[h_{t?1},{?}_{\tau }^z(z_t),c(n_w,t)]$$

$$v(i,t),d(i,t)=f_{{\gamma }_2}(v(i?1,t),d(i?1,t))\text{\hspace{1em}(5)}$$

遞歸過程

狀態級RNN根據以下等式（6）更新其隱藏狀態 $h_t$ 與 $h_{t?1}$。$f_{\theta }$ 是由參數 $\theta$ 參數化的RNN。
$$h_t=f_{\theta }({?}_{\tau }^z(z_t),{?}_{\tau }^x(x_t),h_{t?1})\text{\hspace{1em}(6)}$$

推斷

我們根據上下文 $h_{t?1}$ 和當前話語 $x_t$ 來推斷 $z_t$，并構建 $z_t$ 的后驗分布，通過另一個softmax函數，如等式（7）所示。一旦我們得到了后驗分布，我們應用Gumbel-Softmax來取 $z_t$ 的樣本。D-VRNN和DD-VRNN在它們的先驗上有所不同，但在推斷上沒有不同，因為我們假設在先驗中 $z_t$ 之間的直接轉換而不是在推斷中。
$$z_t|x_t～\text{softmax}({?}_{\tau }^{enc}(h_{t?1}),{?}_{\tau }^x(x_t))\text{\hspace{1em}(7)}$$

這段文字描述了變分遞歸神經網絡（VRNN）的損失函數，以及為了解決變分自編碼器（VAE）中潛在變量消失的問題，如何結合了兩種損失函數：bow-loss和Batch Prior Regularization (BPR)。以下是對該段落的翻譯以及相關公式的解釋：

損失函數

VRNN的目標函數是其在每個時間步的變分下界，如等式（8）所示（Chung等人，2015）。為了緩解VAE中潛在變量消失的問題，我們結合了bow-loss和Batch Prior Regularization (BPR)（Zhao等人，2017，2018）到最終的損失函數中，并引入了可調整的權重 $\lambda$，如等式（9）所示。

$${\mathcal{L}}_{\text{VRNN}}={\mathbb{E}}_{q(z_{\le T}|x_{\le T})}[\log p(x_t|z_{\le t},x_{<t})]+$$
$$\sum _{t=1}^T?\text{KL}(q(z_t|x_{\le t},z_{<t})\Vert p(z_t|x_{<t},z_{<t}))\text{\hspace{1em}(8)}$$

$${\mathcal{L}}_{\text{D-VRNN}}={\mathcal{L}}_{\text{VRNN-BPR}}+\lambda ?{\mathcal{L}}_{\text{bow}}\text{\hspace{1em}(9)}$$

狀態轉移概率計算

一種既能數值表示又能視覺表示對話結構的好方法是構建一個潛在狀態之間的轉移概率表。這樣的轉移概率也可以用來設計在強化學習（RL）訓練過程中的獎勵函數。我們因為D-VRNN和DD-VRNN的先驗不同，所以分別計算它們的轉移表。

D-VRNN

從等式（6）我們知道 $h_t$ 是 $x_{\le t}$ 和 $z_{<t}$ 的函數。結合等式（1）和（6），我們發現 $z_t$ 是 $x_{\le t}$ 和 $z_{<t}$ 的函數。因此，$z_{<t}$ 對 $z_t$ 有一個間接的影響通過 $h_{t?1}$。這個間接影響加強了我們的假設，即前面的狀態 $z_{<t}$ 影響未來的狀態 $z_t$，但也使得恢復一個清晰的結構和解開 $z_{t?1}$ 對 $z_t$ 直接影響變得困難。

為了更好地可視化對話結構并與基于HMM的模型進行比較，我們通過估算二元轉移概率表來量化 $z_{t?1}$ 對 $z_t$ 的影響，其中 $p_{i,j}=\frac{\#(stat{e}_i,stat{e}_j)}{\#(stat{e}_i)}$。分子是有序對（$stat{e}_i,t?1$，$stat{e}_j,t$）的總數，分母是數據集中 $stat{e}_i$ 的總數。我們選擇一個二元轉移表而不是一個更大 $n$ 的 $n$-gram轉移表，因為最近的上下文通常是最相關的，但應該注意的是，與HMM模型不同，我們模型中的轉移程度既不是有限的也不是預先確定的，因為 $z_t$ 捕獲了所有上下文。根據不同的應用，可能會選擇不同的 $n$。

命名實體離散變分遞歸神經網絡（NE-D-VRNN）

在任務導向對話系統中，某些命名實體的存在，如食物偏好，對于確定對話的階段起著關鍵作用。為了確保潛在狀態捕獲此類有用信息，我們在計算等式（9）中的損失函數時，對命名實體賦予更大的權重。這些權重鼓勵重構的話語含有更多正確的命名實體，因此影響潛在狀態有更好的表示。我們將這個模型稱為NED-VRNN（命名實體離散變分遞歸神經網絡）。