
pdf | proj | code
- 本文提出一種新的3D數據表達形式3D Gaussians。每個Gaussian由以下參數組成:中心點位置、協方差矩陣、可見性、顏色。通過世界坐標系到相機坐標系,再到圖像坐標系的仿射關系,可將3D Gaussian映射到相機坐標系,通過對z軸積分,可得到對應Splatting 2D分布。
- 針對3D Gaussians,提出對應的優化方法。去除可見性太低的高斯,對回傳梯度較大的高斯,通過復制,克隆等操作,增強表達能力。
- 針對3D Gaussians,提出對應的光柵化方法。將圖像切分為16 x 16的塊,每個塊內對高斯根據深度進行排序。光柵時,從前向后遍歷,當可見性累加到某個閾值即停止。梯度回傳時從停止塊開始,有后向前遍歷。
目錄
摘要
引言
近期工作
Traditional Scene Reconstruction and Rendering
Neural Rendering and Radiance Fields
Point-Based Rendering and Radiance Fields
Overview
Differentiable 3D Gaussian Splatting
Optimization with Adaptive Density Control of 3D Gaussians
Fast Differentiable Rasterizer for Gaussians
Implementation, Results and Evaluation
Implementation
Results and Evaluation
Real-World Scenes
Synthetic Bounded Scenes
Ablations
Initialization from SfM
Densification
Unlimited depth complexity of splats with gradients
Anisotropic Covariance?
Limitations
摘要
- NeRF效果好,但是訓練和渲染很花時間;特別是對1080p分辨率渲染的場景,現有方法無法實現實時渲染。
- 本文引入三個關鍵部分,實現sota視覺質量、較短訓練時間和1080p分辨率下新視角實時渲染。
- 3D Gaussians。通過camera calibration中產生的稀疏點進行初始化。這種新的3D表達形式在保存NeRF優點的同時,避免了空白空間不必要的計算開銷;
- Optimization。實現3D Gaussian的交替優化和密度控制,優化各向異性協方差矩陣實現對場景的準確表達;
- Rendering。實現快速可見感知渲染算法(fast visibility-aware rendering algorithm),支持各向異性飛濺(anisotropic splatting),同時加速訓練和渲染。
- 本文在多個數據集上,實現sota視覺質量和實時渲染。
引言
- Mesh和點云是最常用的3D場景表達,這種顯式表達非常適合快速GPU/CUDA-based rasterization。另一方面,NeRF可建立連續的場景表達,用volumetric ray-marching優化MLP,實現新視角生成。基于NeRF的高效算法,通常會引入一些新的表達形式,用插值的方式實現連續表達,例如:體素(voxel),hash grids,或點云。這些方法效果不錯,但是渲染中要求的隨機采樣計算開銷大、并且會導致噪聲。本文提出的方法:3D Gaussian可以實現sota的視覺質量和具有競爭力的訓練時間;tile-based splatting solution可以實現1080p的實時渲染。
- 本文所提方法由三個主要部分組成。
- 3D Gaussians:通過Structure-from-Motion (SfM) 相機標定得到的稀疏點云初始化,對于NeRF-synthetic dataset,本文方法在隨機初始化情況下,也可取得較好的結果。3D Gaussian的優點在于(a)可導的體表示;(b)通過映射至2D,實現高效柵格化;(c)可以實施標準的alpha-blending;
- 優化:提出一種優化3D Gaussians參數的方法,參數包括:3D position,opacity alpha,anisotropic covariance和球諧系數(spherical harmonic coefficients)。優化方法:交替執行密度控制步,在優化過程中增加或去除3D Gaussians。
- 渲染:提出一種快速GPU排序算法,受tile-based rasterization方法啟發。實現各向異性紋理飛濺(anisotropic splatting),一種可見性排序(visibility ordering)。受益于排序和alpha-blending,可以實現快速和準確的反向傳播。
近期工作
Traditional Scene Reconstruction and Rendering
- light fields (1996) -> Structure-from-Motion (SfM,2006) -> multi-view stereo (MVS,2007)
- MVS-based方法會重投影(re-project)并融合(blend)輸入圖片到新相機視角,使用幾何引導重投影。?
Neural Rendering and Radiance Fields
- Soft3D (2017,首次提出Volumetric representations) -> 將深度學習技術應用到volumetric ray-marching(2019)-> NeRF (2020,提出importance sampling和postional encoding,但是較大MLP影響了速度) -> MipNeRF360(2022,sota視覺效果,但訓練和渲染時間太長)
- 為了加速訓練或渲染,現有的探索集中在三個方向:稀疏數據結構存儲特征,不同的編碼器和MLP容量。其中,值得一提的方法是InstantNGP(2022),該方法使用hash grid和occupancy grid來加速計算,用一個較小的MLP表示密度和外觀。Plenoxels(2022),使用稀疏體素網格,插值表示連續密度場,并且能夠不使用MLP。
- 盡管上述方法產生了很好的結果,這些方法仍然不能高效表示空白區域。
Point-Based Rendering and Radiance Fields
-blending和體渲染(volumetric rendering)本質上是相同的成像模型。對于體渲染方法:
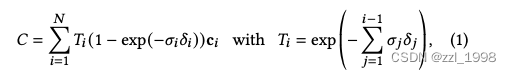
其中是密度,
是透光率,
是顏色,
是相鄰采樣點的間隙。
密度越大,
越接近1,該點越重要;之前點的密度和越大,
越大,該點越不重要。上式可以被重新組織為:
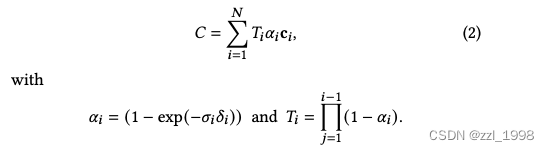
alpha-blending可以表示為:
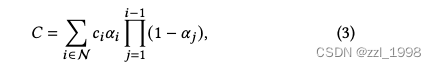
其中,所有點根據前后關系排序,是該點顏色,
是該點所在2D高斯的概率密度乘以該點的不透明性(opacity)。
相較于之前的-blending柵格化方法,本文提出可見性(visibility)排序。另外,本文反向傳播梯度到像素點中的所有splats,柵格化所有各向異性splats。
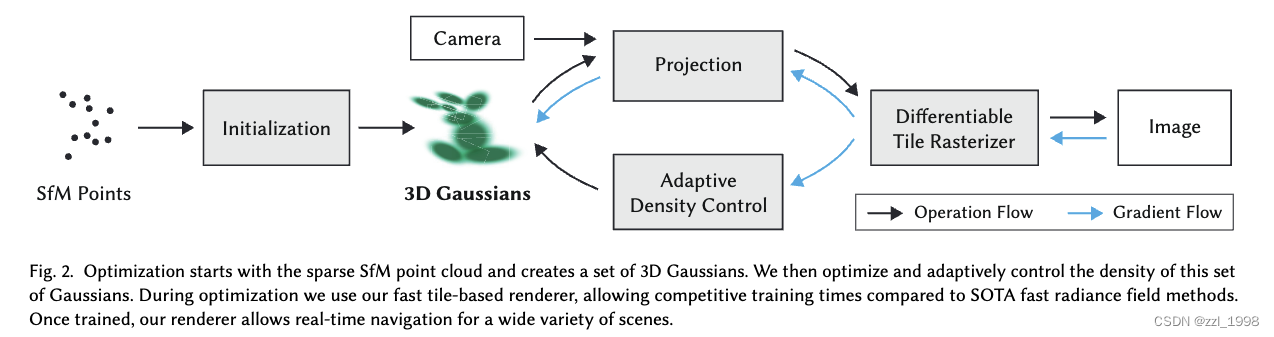
Overview
- Initialization:給定靜態場景的一組圖片,和對應經過SfM校準的相機參數,以及SfM在校準過程中產生的稀疏點云;
- 3D Gaussians:給定稀疏點云,初始化3D Gaussians,每個3D Gaussian由位置mean,協方差矩陣和不透明性
決定;輻射場中指向性外觀部分(顏色),通過spherical harmonics (SH) 表征;
- Optimization:逐步優化3D Gaussians的參數:位置、協方差矩陣、
和SH系數;
- Rendering:tile-based rasterizer,支持根據可見性順序的各向異性splats的
-blending
Differentiable 3D Gaussian Splatting
在世界坐標系下,3D Gaussians由三個系數定義:均值,3D協方差矩陣
和
:
![]()
將世界坐標系下的3D Gaussians轉換到相機坐標下:
![]()
其中,是世界坐標系坐標到相機坐標系坐標的轉換矩陣,
是透視變換的Jacobian矩陣。
參考:EWA Volume Splatting
- View transformation:將世界坐標系下坐標轉換到相機坐標系。假設
是世界坐標系下坐標,
是相機坐標系下坐標,則有仿射變換
,可得
。
- Projective Transformation(透視變換):將相機坐標系下坐標轉換到圖像空間,該轉換不是仿射變換。假設
是圖像空間下坐標,則有
。由于該變換不是放射變換,因此考慮:
,得到局部放射近似,其中
。最終可得
。
協方差矩陣具有物理含義,需要滿足半正定條件。考慮協方差矩陣描述了一個標準球體向橢球體的變化過程,對標準球體先放縮,再旋轉
:
![]()
因此,縮放可以用三維向量描述,也即協方差矩陣的三個特征值。旋轉其實是三個特征向量,它們兩兩正交且模為1,通過分析可由四維向量描述。
綜上,一個3D Gaussian可由三個縮放系數、四個旋轉系數、中心點位置和不透明率
表示。除了上述提到的參數外,本文還用SH系數表示顏色。
Optimization with Adaptive Density Control of 3D Gaussians
- 不透明率
通過sigmoid激活函數映射至0到1之間。
- 損失函數如下:
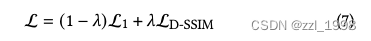
Gaussian的優化過程中,本文考慮以下兩種情況:
異常:移除
小于閾值
的高斯。
- 梯度異常:梯度超過閾值
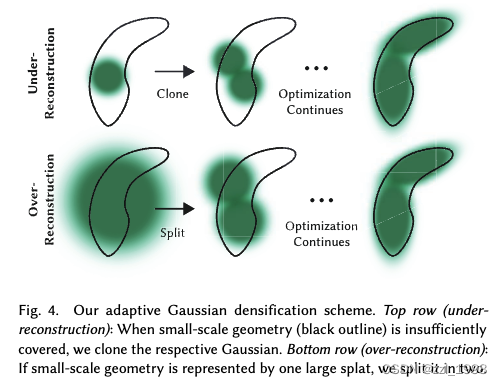
時,本文認為梯度異常,考慮存在under-reconstruction或over-reconstruction:
- under-reconstruction:Gaussians太小了,不能覆蓋必要幾何。本文考慮復制相同大小的Gaussian,新Gaussian放至位置梯度所指方向;
- over-reconstruction:對于方差太大的Gaussians,本文將其拆分為兩個Gaussians,兩個都縮放
,新Gaussian的位置通過在舊Gaussian中采樣決定。
- 特殊情況:
- 漂浮物(floaters)會導致Gaussian密度的異常增加。本文提出,每
?iter,將所有
設置為近似為0的值。在優化后,對于
沒有增大的Gaussian,則根據前述規則去除掉。
- 對于具有非常大worldspace和相機坐標中具有較大footprint的Gaussian也會去除掉。
- 漂浮物(floaters)會導致Gaussian密度的異常增加。本文提出,每

Fast Differentiable Rasterizer for Gaussians
提出一種tile-based rasterizer
- 光柵化:
- 將屏幕劃分為16 x 16塊,一次性預排序所有primitives,避免針對每個像素排序的開銷
- 僅保留有99%置信度的Gaussians
- 用保護帶(guard band)拒絕極端位置的高斯,例如:距離平面太近,或在視錐體之外太遠的高斯;
- 實例化高斯,并賦予每個高斯一個鍵值,包括視覺空間深度和塊ID
- 根據鍵值排序高斯。對于每個塊,得到一個根據深度由近到深排序的列表
- 在光柵化過程中,每個塊使用一個線程去處理,每個線程首先將Gaussians加載到shared memory。對于給定像素點,從前往后遍歷列表,根據
加權求和顏色。當
達到目標飽和值時,該進程停止,得到該像素點的顏色。
- 梯度回傳:從最后一個點,從后往前遍歷列表,選擇對應的Gaussian反傳梯度。
Implementation, Results and Evaluation
Implementation
Pytorch + 用于光柵化的custom CUDA kernels
Results and Evaluation
Real-World Scenes


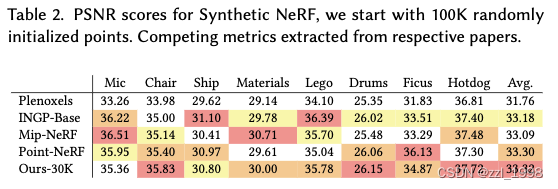
Synthetic Bounded Scenes
- 30K迭代后,每個場景由200-500K Gaussians組成

Ablations
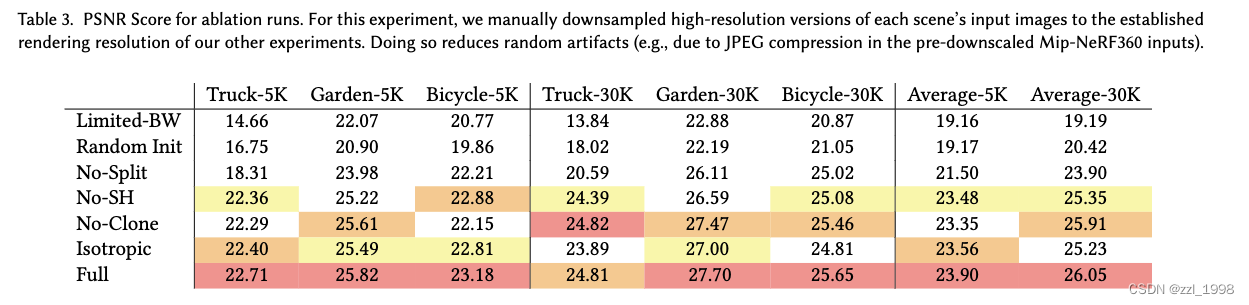
Initialization from SfM

Densification

Unlimited depth complexity of splats with gradients

Anisotropic Covariance?

Limitations
- 對于缺乏訓練數據的場景,存在失真,Mip-NeRF360也存在:

- 存在拉長失真(elongated artifacts),比較臟的高斯(splotchy Gaussians),Mip-NeRF360也有

- 相較于NeRF-based方法,內存開銷大,需要20GB GPU memory



![[ 云計算 | AWS 實踐 ] 基于 Amazon S3 協議搭建個人云存儲服務](http://pic.xiahunao.cn/[ 云計算 | AWS 實踐 ] 基于 Amazon S3 協議搭建個人云存儲服務)




圖像處理的基本操作)





)




