生活如果真能像隊列一樣,那該多好啊。
——————————————————————————————————————————
背包,隊列
可以先看他們的API:都含有一個無參構造函數,添加單個元素的方法,測試集合是否為空的方法和返回集合大小的方法。而Stack和Queue有能刪除集合的特定元素的方法。
它們具有泛型和迭代的特性。
泛型的使用,可以用它們存儲任意類型的數據。
如:Stack , 用Item替換任意數據類型
Stack<String> stack = new Stack<String>();
而類型參數必須被實例化為引用類型。而java具有自動裝箱和自動拆箱的機制,可以在引用類型和對應的原始數據類型之間轉換。
Stack<Integer> stack = new Stack<Integer>();
stack.push(17); //自動裝箱 (int 轉換為 Integer)
int i = stack.pop(); //自動拆箱 (Integer 轉換為 int)
如果集合可迭代,可以使用如foreach循環來逐個訪問集合中的元素,無需手動管理索引或遍歷位置,這樣可以簡化代碼實現。
Queue<String> queue = new LinkedList<>();
// 使用 foreach 循環來遍歷 Queue
for (String element : queue) {System.out.println(element);
}
背包
特點:
- 不支持刪除元素和遍歷操作
- 收集元素并迭代遍歷所有收集到的元素
- 迭代的順序不確定(無序)且與用例無關
- 主要用于統計計算,去重,求平均值或者樣本標準差之類的場景
就理解成一個背包即可,里面各種球,一次放進去一個球,或者一次從里面找自己想要的具有某種特點的球。
Bag<Double> numbers = new Bag<Double>();
while (!StdIn.isEpty()) numbers.add(StdIn.readDouble());
int N = number.size(); // 背包的元素數量double sum = 0.0
for (double x : number)sum += x;
double mean = sum/N;sum = 0.0;
for(double x : number)sum += (x - mean)*(x- mean);
double std = Math.sqrt(sum/(N-1));
隊列(queue)
先進先出隊列是一種基于先進先出(FIFO) 策略的集合類型。
使用場景很常見,尤其是排隊,打印機等待打印或者是計算機某些軟件等待處理的任務。
因為是服務性的策略,所以主打一個公平,先到先得,等的越久越先服務。
Queue<Integer> queue = new Queue<Integer>();
// Enqueue 操作 可以通過add()或offer()方法實現
queue.add("A");
queue.add("B");
queue.offer("C");// dequeue:從隊列的頭部移除并返回一個元素,可以使用remove()或poll()方法來實現
String dequeuedElement = queue.remove();
System.out.println("Dequeued element: " + dequeuedElement);
隊列是一個有序列表,可以用數組或是鏈表來實現。
數組模擬隊列思路
- 隊列本身是有序列表,若使用數組的結構來存儲隊列的數據,則隊列數組的聲明如下圖, 其中 maxSize 是該隊 列的最大容量。
- 因為隊列的輸出、輸入是分別從前后端來處理,因此需要兩個變量 front 及 rear 分別記錄隊列前后端的下標, front 會隨著數據輸出而改變,而 rear 則是隨著數據輸入而改變,如圖所示:
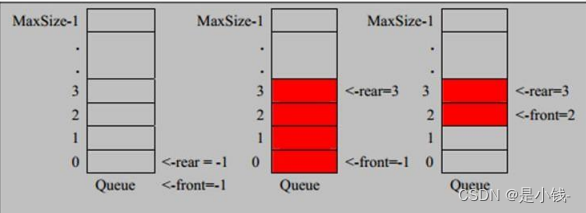
準備工作思路:
-
將front和rear初始化為-1 , 為了表示隊列為空的狀態 (當隊列中添加第一個元素時,front和rear都會更新為0,表示隊列中有一個元素)
-
當 front == rear 則代表隊列為空
-
當 rear == maxSize - 1 則代表隊列為滿
class ArrayQueue {
private int maxSize; // 表示數組的最大容量
private int front; // 隊列頭
private int rear; // 隊列尾
private int[] arr; // 該數據用于存放數據, 模擬隊列// 創建隊列的構造器
public ArrayQueue(int arrMaxSize) {maxSize = arrMaxSize;arr = new int[maxSize];front = -1; // 指向隊列頭部,分析出 front 是指向隊列頭的前一個位置.rear = -1; // 指向隊列尾,指向隊列尾的數據(即就是隊列最后一個數據)
}// 判斷隊列是否滿 (隊列尾指向數組的最大索引)
public boolean isFull() {return rear == maxSize - 1;
}// 判斷隊列是否為空 (初始時,兩指針都為-1,指向同一個位置)
public boolean isEmpty() {return rear == front;
}存入數據思路分析:
1.添加元素時,判斷隊列是不是滿的。若不是,則頭指針不動,用于元素出隊列,將尾指針后移:rear+1
2.再將數據存入 rear 所指的數組元素中
// 添加數據到隊列
public void addQueue(int n) {
// 判斷隊列是否滿if (isFull()) {System.out.println("隊列滿,不能加入數據~");return;}rear++; // 讓 rear 后移arr[rear] = n;
}
出隊列(獲取隊列的數據)代碼:
public int getQueue() {
// 判斷隊列是否空if (isEmpty()) {// 通過拋出異常throw new RuntimeException("隊列空,不能取數據");}front++; // front 后移 滿足先進先出原則。return arr[front];
}
顯示隊列中的所有數據 代碼:
public void showQueue() {// 遍歷if (isEmpty()) {System.out.println("隊列空的,沒有數據~~");return;}for (int i = 0; i < arr.length; i++) {System.out.printf("arr[%d]=%d\n", i, arr[i]);}
}
顯示隊列的頭數據 代碼:
public int headQueue() {if (isEmpty()) {throw new RuntimeException("隊列空的,沒有數據~~");}return arr[front + 1];}
}對于這個代碼所模擬的隊列進行問題分析及方案優化:
- 問題:目前數組使用一次就不能用,沒有出隊列的功能,則沒有達到復用的效果。且如果隊列尾部的空間已滿,而隊列頭部仍有空間,此時無法再添加元素
- 優化方案:將這個數組使用算法,改進成一個環形的隊列 通過取模(%)變成循環的
數組模擬環形隊列
? 對前面的數組模擬隊列進行優化,實現可以復用。成為是一個環形的循環隊列。(通過取模的方式來實現即可)
分析說明:
-
因為是環形結構,滿了會回頭。所以當尾索引的下一個為頭索引時,表示隊列滿了。因此將隊列容量空出一個作為約定。通過這個約定可以得出, (rear + 1) % maxSize == front,代表隊列滿了。
-
rear == front 則代表隊列為空
當你定義了1個長度為5的隊列,已經有了4個元素。這個時候頭指針指著第一個數字,尾指針值向
具體思路如下:
-
將front指向隊列的第一個元素,即front=0
-
將rear指向隊列最后一個元素的后一個位置,即rear=0。(這里需要注意,rear指向的位置實際上是不存儲數據的,只是為了區分隊列空和滿的情況,因此需要浪費一個位置)
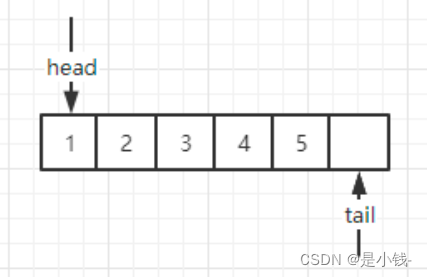
這里比如當你定義了1個長度為5的隊列,已經有了4個元素。這個時候頭指針指著第一個元素,尾指針值向第4個元素后面的位置。這時候你再加一個元素的話,那尾指針就指回了第一個位置,這樣子就出現了rear == front。那你就沒辦法確定到底是隊列滿了還是隊列空了。因此采用(rear + 1) % maxSize == front就表示隊列滿了,此時rear指向的位置實際上是不存儲數據的。-
在網上找到的其他思路:新增一個容量 capacity 字段,并進行維護,當 capacity=size 表示隊列已滿。維護一個標記,或者當 頭指針=尾指針 時同步判斷當前位置是否有元素來判斷當前是隊空還是隊滿。 -
現在使用的方法會浪費一個空間;而新增容量字段需要維護,而標記的方法隊列空和隊列滿的時候需要判斷是那種情況,影響性能。一般使用浪費一個空間的方法,用空間換時間。
-
-
在判斷隊列是否滿時,尾指針的下一個位置會等于頭指針的位置。所以使用**(rear + 1) % maxSize == front**條件,當rear和front相鄰且都指向有數據的位置時,隊列為滿。
public boolean isFull() {return (rear + 1) % maxSize == front; } -
在判斷隊列是否為空時,使用rear == front的條件,當隊列中沒有元素時,front和rear都指向同一個位置。
public boolean isEmpty() {return rear == front; } -
計算隊列中有效數據元素的個數時,使用**(rear + maxSize - front) % maxSize**的公式,由于隊列是循環的,所以隊列的尾部可能在數組的起始位置之前。
計算出隊列尾指針
rear到隊列頭指針front的距離,并進行模運算,得到實際的元素個數。
-
添加數據到隊列
public void addQueue(int n) {// 判斷隊列是否滿if (isFull()) {System.out.println("隊列滿,不能加入數據~");return;}//直接將數據加入arr[rear] = n;//將 rear 后移, 這里必須考慮取模!rear = (rear + 1) % maxSize;
}
獲取隊列的數據, 出隊列
public int getQueue() {// 判斷隊列是否空if (isEmpty()) {// 通過拋出異常throw new RuntimeException("隊列空,不能取數據");}// 這里需要分析出 front 是指向隊列的第一個元素// 1. 先把 front 對應的值保留到一個臨時變量// 2. 然后將 front 后移, 考慮取模!// 3. 將臨時保存的變量返回int value = arr[front];front = (front + 1) % maxSize; return value;
}
顯示隊列的所有數據
public void showQueue() {// 遍歷if (isEmpty()) {System.out.println("隊列空的,沒有數據~~");return;}for (int i = front; i < front + size() ; i++) {// 使用 i % maxSize 的目的是確保索引值在循環隊列的有效范圍內
//假設隊列的最大大小為 5,且隊列起始位置front是2,不取模的話,那就超出了隊列范圍,應該回到隊列的開頭,則需要取模。System.out.printf("arr[%d]=%d\n", i % maxSize, arr[i % maxSize])}
}// 求出當前隊列有效數據的個數
public int size() {// rear = 2// front = 1// maxSize = 3return (rear + maxSize - front) % maxSize;
}
顯示隊列的頭數據
public int headQueue() {// 判斷if (isEmpty()) {throw new RuntimeException("隊列空的,沒有數據~~");}return arr[front];}
}————————————————————————————————————
那這樣子是不是就有機會了



 D. Absolute Beauty)


)
和遞減運算符(--))











)