并查集簡介
并查集是一種可以動態維護若干個不重疊的結合,并支持合并與查詢的數據結構
并查集是一種樹狀的數據結構,可以用于維護傳遞關系以及聯通性。
并查集有兩種操作:
find:查詢一個元素屬于哪個集合merge:合并兩個集合
模板
find函數
int find(int x)
{if(x == fa[x]) return x;reutnr fa[x] = find(fa[x]);
}
merge函數
void merge(int x, int y)
{int px = find(x), py = find(y);if(px != py) fa[px] = py;
}
模板題
村村通
對于這道題我們只需要求連通塊的數量,然后將這幾個聯通快看成點,聯通n個點需要n-1條邊
#include <iostream>
#include <cstring>using namespace std;
const int N = 1010;
int p[N], st[N];int find(int x)
{if(x == p[x]) return x;return p[x] = find(p[x]);
}int main()
{// freopen("1.in", "r", stdin);while(1){memset(st, 0, sizeof st);int n, ans = 0;scanf("%d", &n);if(n == 0) return 0;else{int m; scanf("%d", &m);for(int i = 1; i <= n; ++ i) p[i] = i;for(int i = 0; i < m; ++ i){int x, y; scanf("%d%d", &x, &y);int a = find(x);int b = find(y);if(a != b) p[a] = b;}//統計聯通塊的數量for(int i = 1; i <= n; ++ i){int x = find(i);if(!st[x]) ans ++, st[x] = 1;;}cout << ans - 1 << endl;}}
}
P1551 親戚
親戚的親戚是親戚,親戚這種關系具有傳遞性,如果具有親戚關系就將合并。
#include <iostream>using namespace std;const int N = 5010;int p[N];
int n, m, t;int find(int x)
{if(x != p[x]) p[x] = find(p[x]);return p[x];
}int main()
{cin >> n >> m >> t;for(int i = 1; i <= n; ++ i) p[i] = i;for(int i = 0; i < m; ++ i){int a, b;cin >> a >> b;int fa = find(a);int fb = find(b);p[fa] = fb;}for(int i = 0; i < t; ++ i){int a, b;cin >> a>> b;int fa = find(a);int fb = find(b);if(fa != fb) puts("No");else puts("Yes");}return 0;
}
836. 合并集合
#include <iostream>using namespace std;const int N = 1e5+10;int n,m;
int p[N];int find(int x)
{if(p[x] != x ) p[x] = find(p[x]);return p[x];
}int main(int argc, const char * argv[]) {scanf("%d%d",&n,&m);for(int i = 0; i < n; i ++) p[i] = i;while(m--){char op[2];int a,b;scanf("%s%d%d",op,&a,&b);if(op[0] == 'M') p[find(a)] = find(b);else{if(find(a) == find(b)) cout<<"Yes"<<endl;else puts("No");}}return 0;
}
837. 連通塊中點的數量
這道題目比前面的幾道模板題目需要多維護一個信息,在進行merge時我們需要將更新作為被添加枝的樹的cnt
兩個bug調了一個小時最后看了下評論區收獲頗豐
1、合并兩個集合時
如果沒有按照下面的寫法即省去這一步a=find(a),b=find(b);
則合并根節點的順序與更新更新集合得順尋不能互換,
必須要先把原來根節點中元素的數量加到所要合并的
根節點上去再把根節點合并
a=find(a),b=find(b);
cnt[b]+=cnt[a];
p[a]=b;
2、路徑壓縮
一定不要忘記路徑壓縮不然會超時!!!
#include"bits/stdc++.h"
using namespace std;
const int N=1e5+10;
int p[N],cnt[N];
int n,m;
int find(int x)
{if(p[x] != x) p[x] = find(p[x]);return p[x];
}
int main()
{cin.tie(0);cin>>n>>m;for(int i=1;i<=n;i++) {p[i]=i;cnt[i]=1;}while(m--){string str;int a,b;cin>>str;if(str=="C"){cin>>a>>b;if(find(a)!=find(b)) {a=find(a),b=find(b);cnt[b]+=cnt[a];p[a]=b;}}else if(str=="Q1"){cin>>a>>b;if(find(a)==find(b)) cout<<"Yes"<<endl;else cout<<"No"<<endl;}else{cin>>a;cout<<cnt[find(a)]<<endl;}}return 0;
}
邊帶權并查集
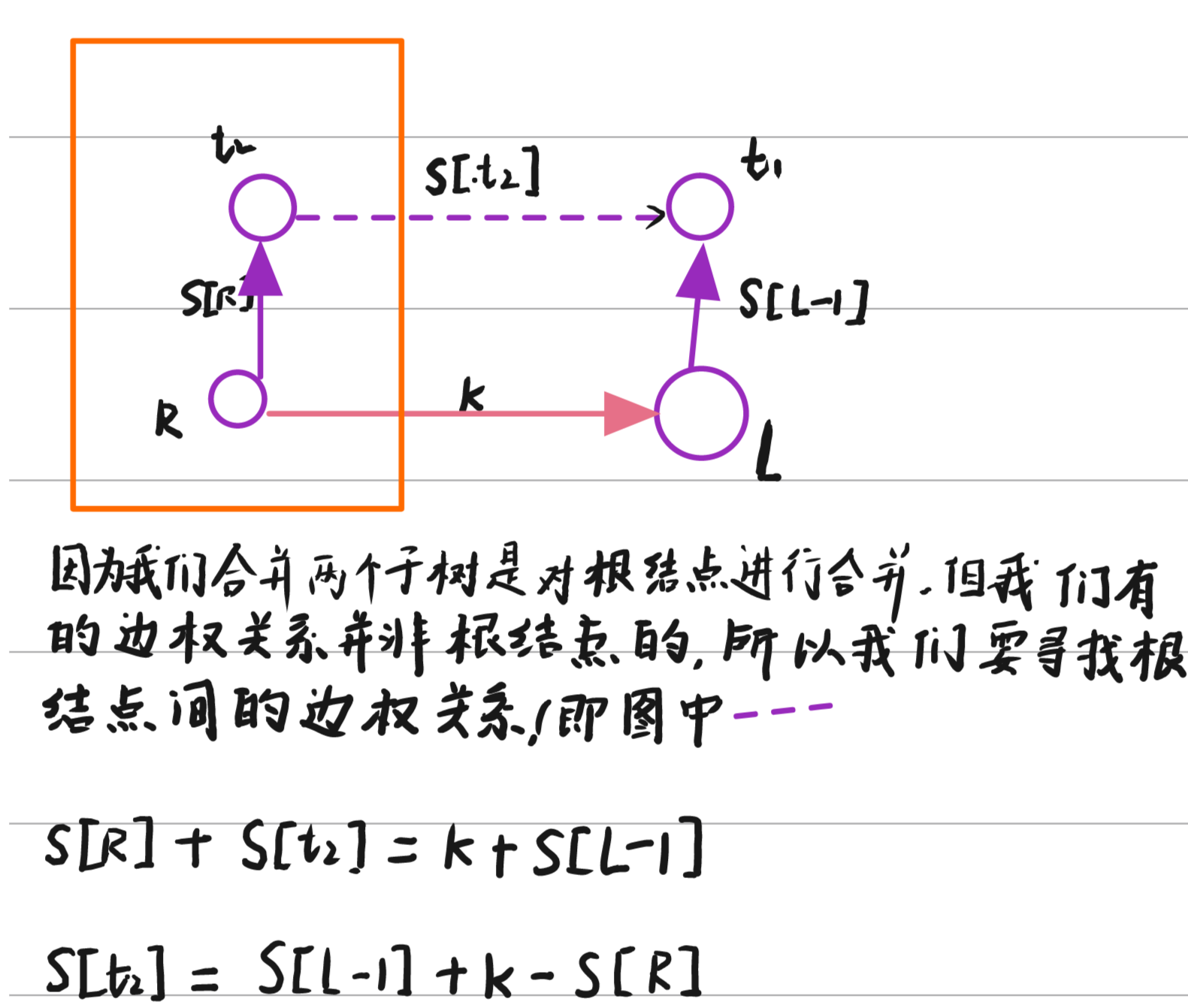
推導部分和
這道題的是帶邊權并查集的應用,比較難想到的是建圖
對于每個區間l, r,k, 我們可以由前綴和s[r] - s[l - 1] = k,我們從r連一條l-1的邊
#include <iostream>using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
//p[N]數組用來做并查集
int p[N], n, m, q;
//s[N]數組是當前點到根結點的權值和,也是前綴和
LL s[N];//并查集的查詢操作(帶路徑壓縮)
int find(int x)
{if(x == p[x]) return x;else{int t = find(p[x]);s[x] += s[p[x]];p[x] = t;return t;}
}int main()
{// freopen("1.in", "r", stdin);cin >> n >> m >> q;for(int i = 1; i <= n; ++ i) p[i] = i;for(int i = 0; i < m; ++ i){int l ,r;LL k; cin >> l >> r >> k;int t1 = find(l - 1), t2 = find(r);if(t1 != t2){p[t2] = t1;s[t2] = s[l - 1] - s[r] + k;}}while(q --){int l, r;cin >> l >> r;int t1 = find(l - 1), t2 = find(r);if(t1 != t2) puts("UNKNOWN");else printf("%lld\n", s[r] - s[l - 1]);}return 0;
}
P1196 [NOI2002] 銀河英雄傳說
這道題目比較特殊是每個集合是一條鏈,一條鏈也是一棵樹,不過是樹的特殊形態,我們可以把每一列看作一個集合,用并查集去維護,另外題目中需要知道兩個點之間的點有多少個,這里我們就還需要額外維護每個點到根節點路徑上的權值,因為我們這里的并查集已經進行優化即使用了路徑壓縮,并且邊權都是1,所以在維護每個點到根節點的路徑上的權值時,我們還需要用到一個集合中元素的個數,也就是還需要額外維護集合中元素個數。
綜上我們需要額外維護兩個信息:
d[x]:表示x到根節點的邊權求和size[x]:表示以x為根的子樹中節點數量
#include <bits/stdc++.h>
#define ls p<<1
#define rs p<<1|1
#define PII pair<int, int>
#define ll long long
#define ull unsigned long long
#define endl '\n'
#define db double
using namespace std;const int N = 30010;
int fa[N], d[N], size[N],t;void init()
{for(int i = 1; i <= N - 1; ++ i) fa[i] = i, size[i] = 1;
}int find(int x)
{if(x == fa[x]) return x;int root = find(fa[x]);d[x] += d[fa[x]];return fa[x] = root;
}void merge(int x, int y)
{int px = find(x), py = find(y);if(px == py) return;fa[px] = py;d[px] = size[py];size[py] += size[px];
}void solve()
{cin >> t;init();for(int i = 1; i <= t; ++ i){char op;int x, y;cin >> op >> x >> y;if(op == 'M') merge(x, y);else{int px = find(x), py = find(y);if(px != py) cout << -1 << endl;else cout << abs(d[x] - d[y]) - 1 << endl; } }
}int main()
{ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
// freopen("1.in", "r", stdin);
// cin >> t;
// while(t --) solve(); return 0;
}
并查集的拓展域
P2024 [NOI2001] 食物鏈
這是一道并查集的拓展域的題目也可以用帶權并查集去做
普通并查集維護的是不相交集合,是一種傳遞性的關系如親戚的親戚是親戚
天敵的天敵是食物,是一種環形的關系
我們如果用拓展域來解決這道題目的話可以用3個并查集來維護3種關系,第一種是同類關系,第二種是食物關系,第三種是天敵
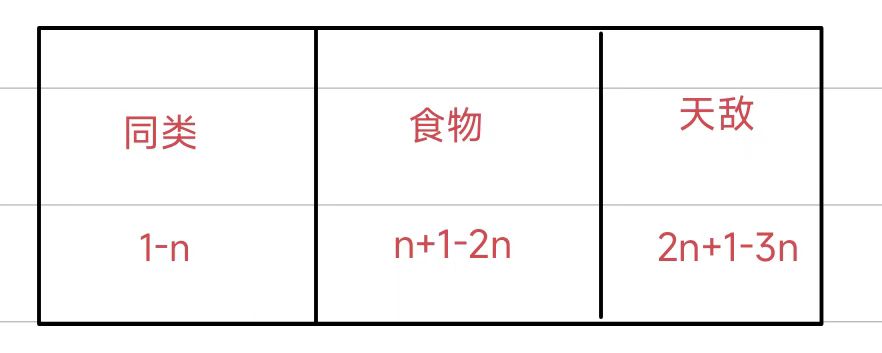
我們不用真開三個并查集,我們可以將三個并查集開到一個數組里,下標的范圍代表不同的集合
#include <iostream>using namespace std;
const int N = 5e4 + 10;
int p[N * 3], ans, k, n;//1--n代表x的同類,n + 1 -- 2n代表x的食物, 2n + 1 -- 3n代表x的天敵
int find(int x)
{if(x == p[x]) return x;return p[x] = find(p[x]);
}
void merge(int x, int y)
{int px = find(x), py = find(y);p[py] = px;
}
int main()
{cin >> n >> k;for(int i = 1; i <= 3 * n; ++ i) p[i] = i;for(int i = 0; i < k; ++ i){int d, x, y;scanf("%d%d%d", &d, &x, &y);if(x > n || y > n) ans ++;//x、y是同類else if(d == 1){//如果根據前面的信息,我們可以知道y在x的食物域,//或者y在x的天敵域中,說明這句話是假話if(find(x + n) == find(y) || find(x + n + n) == find(y)) ans ++;//如果根據前面的信息,不能判斷這句話是錯誤的,那么就講這句話//當成對的并且更新x的三個域else{//y在x的同類域中merge(x, y);//y的食物和x的食物是同類merge(x + n, y + n);//y的天敵和x的天敵是同類merge(x + n + n, y + n + n);}}//如果x吃yelse{//若果y在x的同類域或者,y在x的天敵域說明這句話是假話if(find(x) == find(y) || find(x + n + n) == find(y)) ans ++;//這句話是真話就更新x的三個域else{//y在x的食物域中merge(x + n, y);//y的食物是x的天敵merge(x + n + n, y + n);//y的天敵是x的同類merge(x, y + n + n);}}}cout << ans << endl;return 0;
}
例題團伙
#include <iostream>
using namespace std;
const int N = 2010;
int p[N];
bool st[N];
int find(int x)
{if(p[x] == x) return p[x];return p[x] = find(p[x]);
}
void merge(int x, int y)
{int px = find(x), py = find(y);if(px != py) p[px] = py;
}int main()
{// freopen("1.in", "r", stdin);int n, m;scanf("%d%d", &n, &m);for(int i = 1; i <= 2 * n; ++ i) p[i] = i;for(int i = 0; i < m; ++ i){char op; int x, y;cin >> op >> x >> y;if(op == 'F'){merge(x, y);// merge(x + n, y + n);}else{merge(x + n, y);merge(x, y + n);}}// for(int i = 1; i <= n; ++ i) cout << i << ' ' << find(i) << endl; int cnt = 0;for(int i = 1; i <= n; ++ i)if(!st[find(i)]){cnt ++;st[find(i)] = 1;}cout << cnt << endl;return 0;
}
P5937 [CEOI1999] Parity Game
題目的具體思路如下:考慮一段連續區間的1個數的奇偶,可以轉化為考慮考慮兩個端點前綴和的奇偶性上,分為兩種情況,如果[l, r]區間內1的個數為偶數,說明sum[r]和sum[l - 1]包含1的個數的奇偶性相同,反之若為奇數則兩個包含1的個數的奇偶性相反,我們知道奇偶性具有傳遞性,這樣我們就可以種類并查集來維護,注意n的范圍比較大,但是實際的需要用到的點的個數是比較小的,這里我們需要離散化一下。
#include <bits/stdc++.h>
#define LL long long
using namespace std;const int N = 1e4 + 10;
int p[N * 2 + 10], n, m, k;
map<int, int>mp;
int b[N * 2];struct wy
{int l, r, op;
}q[N];int find(int x)
{if(x != p[x]) p[x] = find(p[x]);return p[x];
}void merge(int x, int y)
{int px = find(x), py = find(y);p[py] = px;
}int query(int x)
{return lower_bound(b + 1, b + 1 + k, x) - b;
}
void solve()
{scanf("%d%d", &n, &m);for(int i = 1; i <= m; ++ i){int l, r, op;char s[5];scanf("%d%d%s", &l, &r, s);if(s[0] == 'e') op = 1;else op = 2;q[i] = {--l, r, op};b[++ k] = l;b[++ k] = r;} sort(b + 1, b + 1 + k);k = unique(b + 1, b + 1 + k) - (b + 1);for(int i = 1; i <= 2 * k; ++ i) p[i] = i;for(int i = 1; i <= m; ++ i){int l = query(q[i].l), r = query(q[i].r), op = q[i].op;if(op == 1) {if(find(l) == find(r + k) || find(r) == find(l + k)){printf("%d", i - 1);return;}else{merge(l, r);merge(l + k, r + k);}}else{if(find(l) == find(r) || find(r + k) == find(l + k)){printf("%d", i - 1);return;}else{merge(l, r + k);merge(r, l + k); }} }printf("%d", m);
}
int main()
{
// freopen("1.in", "r", stdin);solve(); return 0;
}
應用
P1955 [NOI2015] 程序自動分析
這道題目是相等關系,相等關系也具有傳遞性,明顯我們可以用并查集來維護。
我們可以先對處理相等,然后去查詢不相等的是否在一個集合里面如果在一個集合里面則說明這樣的點是不存在的。這道題目的數據的范圍很大,但實際用到的很少,我們需要對數據進行離散化。
#include <bits/stdc++.h>
#define LL long long
using namespace std;const int N = 1e6 + 10;
int n, m, p[N], a[N], k, tot;
struct wy{int x, y, e;
}q[N];int find(int x)
{if(x != p[x]) p[x] = find(p[x]);return p[x];
} void merge(int x, int y)
{int px = find(x), py = find(y);p[py] = px;
}void solve()
{scanf("%d", &n);for(int i = 1; i <= n; ++ i){int x, y, e;scanf("%d%d%d", &x, &y, &e);a[++ tot] = q[i].x = x;a[++ tot] = q[i].y = y;q[i].e = e; }sort(a + 1, a + 1 + tot);tot = unique(a + 1, a + 1 + tot) - a - 1;for(int i = 1; i <= tot; ++ i) p[i] = i;for(int i = 1; i <= n; ++ i){q[i].x = lower_bound(a + 1, a + tot + 1, q[i].x) - a - 1;q[i].y = lower_bound(a + 1, a + tot + 1, q[i].y) - a - 1;if(q[i].e == 1){merge(q[i].x, q[i].y);}}for(int i = 1; i <= n; ++ i){int x = q[i].x;int y = q[i].y;if(q[i].e == 0 && find(x) == find(y)){puts("NO");return;}}puts("YES");
}int main()
{
// freopen("1.in", "r", stdin);scanf("%d", &k);while(k--) solve(); return 0;
}
P1525 [NOIP2010 提高組] 關押罪犯
貪心+并查集,我們優先選擇邊權最大的罪犯,首先查詢他們是否已經在一個集合 如果不在,分別將他們放進不同監獄(集合),如果在則說明我們已經找到了答案
#include <bits/stdc++.h>
#define ls p<<1
#define rs p<<1|1
#define PII pair<int, int>
#define ll long long
#define ull unsigned long long
#define endl '\n'
#define db double
using namespace std;const int N = 1e6 + 10, e = 20010;struct wy
{int x, y, val;bool operator < (const wy & t) const{return t.val < val;}
}a[N];int p[N + 1];
int n, m;void init()
{for(int i = 1; i <= N; ++ i) p[i] = i;
}int find(int x)
{if(x == p[x]) return x;return p[x] = find(p[x]);
}void merge(int x, int y)
{int px = find(x), py = find(y);if(px != py) p[py] = px;
}void solve()
{cin >> n >> m;for(int i = 1; i <= m; ++ i){int x, y, val; cin >> x >> y >> val;a[i] = {x, y, val};}sort(a + 1, a + 1 + m);init();for(int i = 1; i <= m; ++ i){int x = a[i].x, y = a[i].y, val = a[i].val;int px = find(x), py = find(y);if(px == py) {cout << val << endl;return;}else{merge(y + n, x);merge(x + n, y);}}cout << 0 << endl;
}
int main()
{ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
// freopen("1.in", "r", stdin);
// cin >> t;
// while(t --) solve(); return 0;
}



















