數據結構的理解

數據本身是雜亂無章的，需要結構進行增刪查改等操作更好的管理數據；

比如：在程序中需要將大量的代碼（數據）通過結構進行管理；
再比如：定義1000個整型變量的數組，我們可以對數組進行刪除某一個數據，在某一個數據后面插入新的數據等等操作。這些都是數據結構的體現。

數據結構是用來在計算機中存儲和管理數據的，這種存儲和管理的方式有很多種，我們后面會一一學到比如：線性表、數、圖、哈希等

數組是最基礎的數據結構；

算法理解

算法是一個良好計算的過程，我們可以將數據結構作為放著數據的容器，而算法就是用來如何才能讓我們良好的從容器中獲取和管理數據的這么一個過程就叫做算法

因此：有數據結構的地方就有算法，數據結構和算法不分家

算法重要性

在筆試和面試中是必考的，是以編程題的形式進行考察，我們要好好磨礪算法，做到手撕代碼 <:

學好算法秘籍：

1.死磕代碼
2.遇到算法題莫慌，帶著思考進行畫圖。
3.看關于算法和數據結構的書藉
4.使用各大OJ平臺進行刷題（用OJ平臺刷題的魅力：只需要寫入內部的邏輯代碼即可，其他的平臺都已經定義好了）

自己下去將輪轉數組進行單獨實現
如何衡量算法的好壞呢？ ----->用復雜度進行衡量

復雜度理解

而復雜度又包含時間復雜度和空間復雜度
時間復雜度主要衡量一個算法的運行快慢；
空間復雜度主要衡量一個算法運行所需要的額外空間
隨著時代的發展，我們對空間的關注已經不是大頭了，時間才是，注意不是不關注！（也就是摩爾定律）

時間復雜度理解

時間復雜度是一個函數表達式T(N),這個與數學中的定義的一次函數和二次函數是一樣的，它是用來衡量程序的運行效率。它是一個粗估的值，不是精確的值。
為什么不去計算程序的運行時間呢？

1.因為程序的運行時間和編譯環境和運行機器的配置都有關系，
比如：同一個算法程序，用一個老的編譯器進行編譯和新的編譯器編譯，在同樣的運行機器下程序運行時間不同
2.同一個算法程序，在不同的運行機器下（在一個老低配置機器和新高配置機器的情況下）使用同一個編譯器進行編譯，程序運行時間也會不一樣
3. 并且計算程序的運行時間只能在程序運行之后才能知道，不能在寫程序之前就知道大概的運行時間是多少。

總結：程序的運行時間是不確定的

時間復雜度T(N)到底怎么去計算呢？
T(N) = 每條語句的運行時間 * 運行次數
前面我們知道運行時間是不確定的，所以將運行時間去掉，所以
T(N) = 程序的運行次數

這個程序的時間復雜度T(N) = N^2 + 2N + 10
因為2N + 10 對時間復雜度的影響很小，所以忽略不計，最終：T(N) = N^2

因此，對于時間復雜度來說，是一個粗估的值，爭對這種情況，我們有了大O的漸進表示法的計算法則進行計算

大O的漸進表示法

大O的計算規則：

1. 時間復雜度T(N) 中，只保留最高項，去掉最低項，包括常數項
2. 如果最高項的常數系數存在且不是1，則去除這個項目的常數系數
3. 如果T(N) 中只有常數項，用常數1代表所有的加法常數。 O(1)來表示

判斷高階項的方法：對結果影響最大就是高階項

大O的漸進表示法在空間和時間上都可以用
時間復雜度舉例：

以下是常見時間復雜度的計算：

T(N) = 2N + 10 根據法則2：O(N)

如果T(N) 中存在兩個變量，不確定這兩個變量的大小，則這兩個變量都可以表示，例如：O(M + N), M 和 N 都是變量，具體看題目中是如何定義M和N 的大小，比如：M >> N, 則為O(M),反之則為O(N);在有一種情況就是M == N， 則為O(M+N)。

T(N) = 100, 根據法則3：O(1)

請寫出查找字符長度的時間復雜度

這里T(N) 的大小取決于你所要查找的位置，
比如：
查找的字符的位置在最后一個位置，則為O(N)
查找的字符的位置在第一個位置，則為O(1)
查找的字符的位置在中間位置，則為O(1/2 * N) = O(N)

最好情況： O(1)
最壞情況： O(N)
平均情況： O(N)

總結 通過上面我們會發現，有些算法的時間復雜度存在最好、平均和最壞情況。 最壞情況：任意輸入規模的最大運行次數(上界)
平均情況：任意輸入規模的期望運行次數 最好情況：任意輸入規模的最小運行次數(下界)
大O的漸進表示法在實際中一般情況關注的是算法的上界，也就是最壞運行情況。

在看看冒泡排序的時間復雜度：

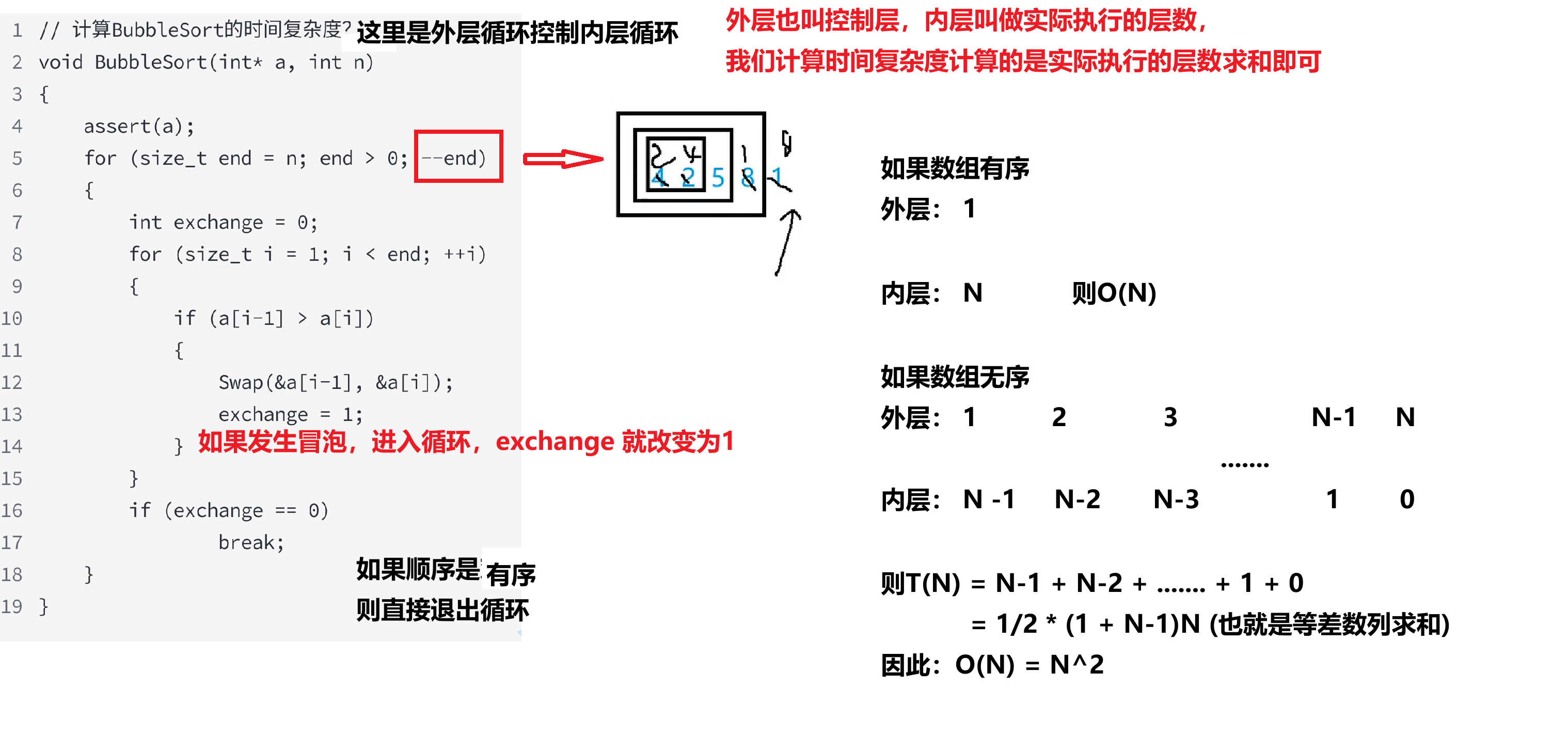
因此，我們取得是上界的情況：O(N^2)

再看看這道題

這里需要注意的是：
課件中和書籍中 log2 n 、 log n 、 lg n 的表示
當n接近?窮?時，底數的??對結果影響不?。因此，?般情況下不管底數是多少都可以省略不 寫，即可以表?為 log n
不同書籍的表??式不同，以上寫法差別不?，我們建議使? log n
還有一個原因是：鍵盤中敲不出底數

到這里時間復雜度的計算就夠夠用了

空間復雜度

空間復雜度計算規則基本跟時間復雜度類似，也使??O漸進表?法。
注意：我們計算空間復雜度時只計算函數運?時所需要的棧空間，存儲參數、局部變量、?些寄存器信息和非遞歸函數調用的棧幀等都是在函數運行時的內容。
因此空間復雜度主要通過函數在運?時候顯式申請的額外空間來確定，也就是函數定義的下面那一部分

以下是常見的空間復雜度的計算：

常見的空間復雜度計算

通過動態內存申請內容也會涉及到空間復雜度的計算
例如：

常?復雜度對?：

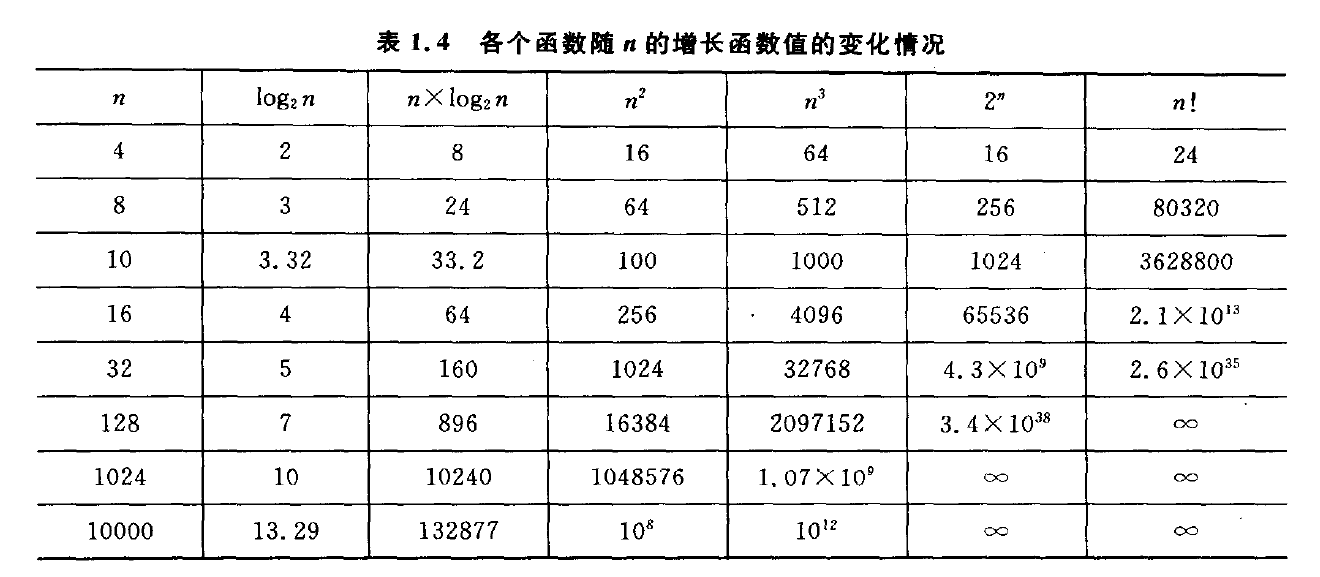
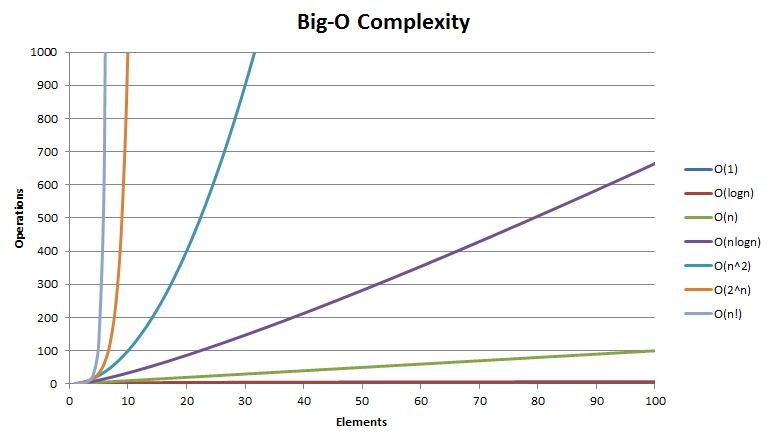
總結：隨著n的增加，各種的復雜度的變化趨勢也大不相同；隨著n的增加，變化越緩的復雜度代表著在程序運行時的效率高；越陡的效率低

關于復雜度的相關算法題:

輪轉數組

思路1:

	時間復雜度 O(n^2)循環K次將數組所有元素向后移動?位（代碼不通過）

核心代碼如下：

void rotate(int* nums, int numsSize, int k) {while(k--)//直到輪轉結束后就停止{int end = nums[numsSize-1];for(int i = numsSize - 1; i > 0; i--)//這里是整體向后移的操作，起始位置在最后一位，直到將第一個數據移到第二位后就結束{nums[i] = nums[i - 1];//將一位的數據移到后一位}nums[0] = end;//將最后的移到第一位}
}

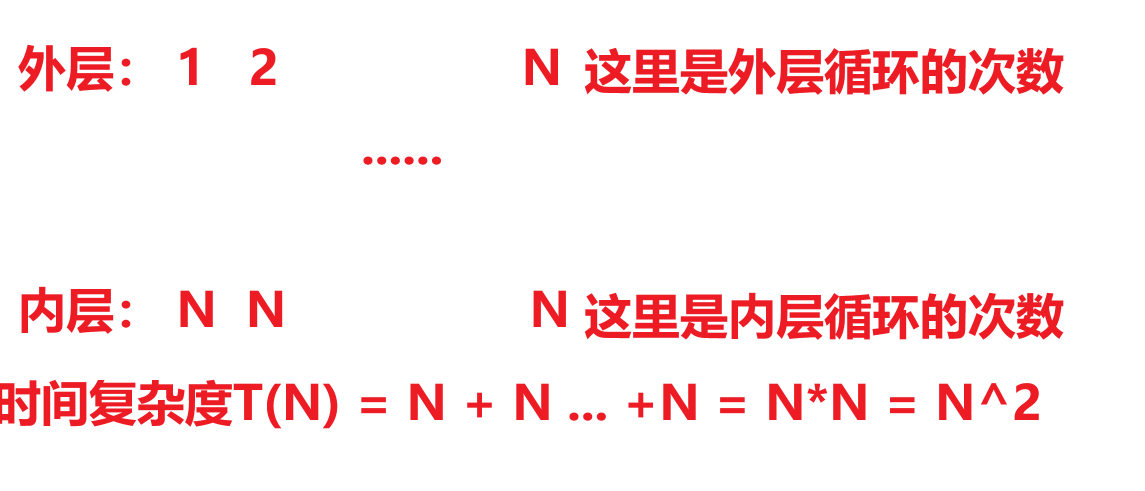
思路2：

空間復雜度 O(n)
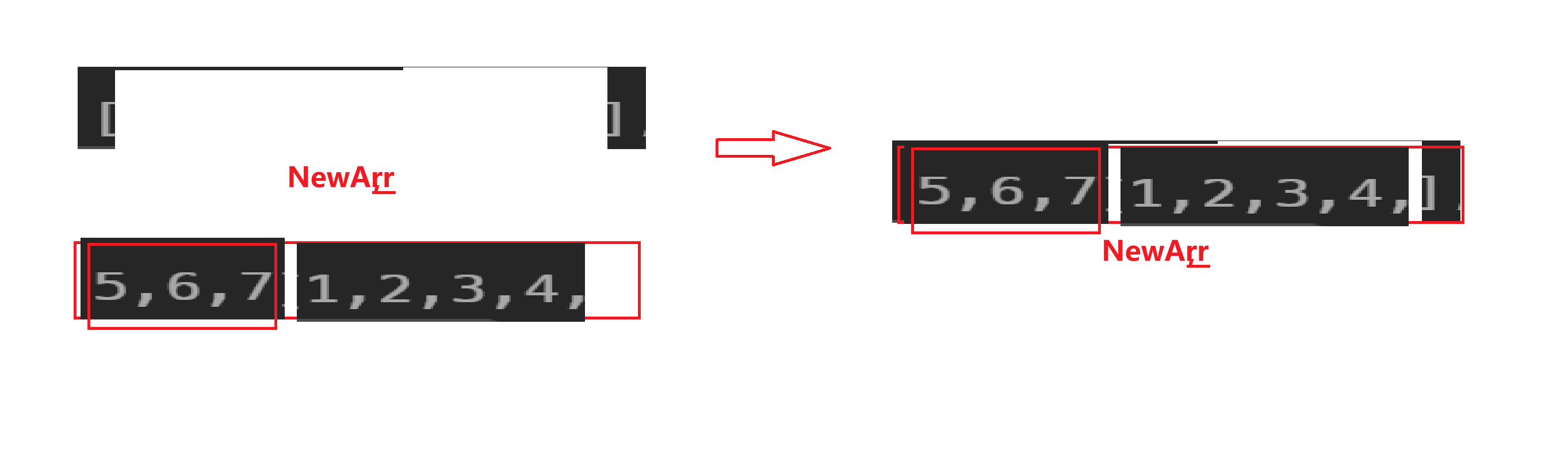
申請新數組空間，先將后k個數據放到新數組中，再將剩下的數據挪到新數組中

核心代碼：

void rotate(int* nums, int numsSize, int k) {int NewArr[numsSize];for(int i = 0; i < numsSize; i++){NewArr[(k + i) % numsSize] = nums[i];//這里是將原數組中的數據放入到新數組下標為(k + i) % numsSize中}for(int i = 0; i < numsSize; i++){nums[i] = NewArr[i]; //再放到原數組中去}}

思路3：

逆置：是指將開始的位置(begin) 和末尾的位置(last)相互置換，多次置換時需要begin++，last–。

空間復雜度 O(1)
先將前n-k個逆置：5 6 7
再將后k個逆置 ：4 3 2 1
最后將整體逆置 ：5 6 7 1 2 3 4

核心代碼：

//逆置的過程可以分裝成一個函數
void reverse(int* nums, int begin, int end)
{while(begin < end) {int tmp = nums[begin];nums[begin] = nums[end];nums[end] = tmp;begin++;end--;}   }void rotate(int* nums, int numsSize, int k) {k = k % numsSize;//先將前n-k個進行逆置reverse(nums, 0, numsSize - 1 - k);//這里傳的是數組的下標//再將后k個進行逆置reverse(nums, numsSize - k, numsSize - 1);//最后整體進行逆置reverse(nums, 0, numsSize - 1);
}

假設數組的個數非常大，有n個，我們從頭 和 尾 兩兩逆置，總共逆置了1/2 * n次，所以時間復雜度為O(N), 我們也沒有額外申請空間，所以空間復雜度為O(1)